Grundlagen sozialwissenschaftlicher Methodologie - Glossar/Korrelation
Vorheriges Kapitel: 2.11 Kausalität
Contents
2.12 Korrelation
Verfasst von Andrea Payrhuber et al.
(lat. con = zusammen; relatio = Bericht, Beziehung)
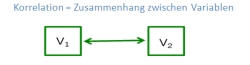
Eine Korrelation liegt dann vor, wenn
- zwei Phänomene gleichzeitig auftreten und
- in einem wechselseitigem Zusammenhang zueinander stehen (miteinander variieren)
Die Phänomene werden mittels Variablen[1] erfasst und messbar gemacht.
Eine Korrelation ist eine mathematische Darstellung ausgedrückt in Variablen, die keine Aussage über die funktionale oder kausale Abhängigkeit der Variablen voneinander erlaubt. Das bedeutet, eine hohe Korrelation zeigt, dass zwei Phänomene gleichzeig auftreten. Es wird aber nichts darüber ausgesagt, welches Phänomen das andere bedingt. Ursache und Wirkung sind nicht bestimmt.
Die Stärke des Zusammenhangs wird mittels statistischer Berechnung über den Korrelationskoeffizienten (r) ermittelt. Gängig Korrelationskoeffizienten können Werte von +1 für maximale positive Korrelation und 1 für maximale negative Korrelation annehmen.
Bei einer positiven Korrelation gilt: Je höher der Wert der einen Variablen, desto höher auch der Wert der anderen Variablen.
Bei einer negativen Korrelation gilt: Je höher der Wert der einen Variablen, desto niedriger der Wert der anderen Variablen.
Referenzstudien:
Durkheim, Émile 1973. Der Selbstmord. Neuwied: Luchterhand.
Jahoda, Marie, Lazarsfeld, Paul Felix, Zeisel, Hans. 1975. Die Arbeitslosen von Marienthal. Frankfurt am Main: Suhrkamp.
Verweise:
[1] Siehe Kapitel 2.23
Inhalt
2.12.1 Beispiele für Korrelationen
Verfasst von Andrea Payrhuber et al.
Beispiel Marienthal:
Die müde Gesellschaft ist apathisch und legt wenig Wert auf Pflege. Die beiden Phänomene verstärken sich gegenseitig. Je apathischer desto weniger Antrieb zur Pflege. Je ungepflegter desto stärker die Apathie.
Es zeigt sich in der Studie bei den Arbeitslosen ein Zusammenhang zwischen den Phänomenen "Apathie" und Verlust der Zeitstruktur. Je mehr "Apathie" desto weniger Zeitstruktur. Je weniger Zeitstruktur desto höhere "Apathie". Diese Wechselseitigkeit macht den Unterschied zur Kausalität aus. Wäre "Apathie" z.B. als Krankheitsbild bekannt, welches das Zeitgefühl der Betroffenen negativ beeinflusst, würde man von Kausalität sprechen, d.h. man würde davon ausgehen, dass die "Apathie" die Ursache für den Verlust der Zeitstruktur (=Wirkung) der Betroffenen ist.
Beispiel Einkommen und Bildung:
hohe Bildung - hohes Einkommen (= pos. Korrelation) Je höher die Bildung desto höher ist das Einkommen das man erhält. Je höher das Einkommen desto intensiver ist die Weiterbildung. Der Bildungsgrad und mit ihm wiederum das Einkommen steigen an. Mit dem steigenden Einkommen steigt wiederum die Motivation und Notwendigkeit zur Weiterbildung.
hohe Bildung - wenig Kinder (= neg. Korrelation) Je höher die Bildung desto weniger Kinder in einer sozialen Gruppe. Je weniger Kinder in dieser sozialen Gruppe desto mehr Bildung.
2.12.2 Fehlinterpretation bei Korrelationen
Verfasst von Andrea Payrhuber et al.
Bei Korrelationen ergeben sich folgende Gefahren für Fehlinterpretationen:
Korrelation als Kausalität interpretiert
Einer der häufigsten Fehler in den Sozialwissenschaften ist es, Korrelationen als Kausalität zu interpretieren.
Scheinkorrelation
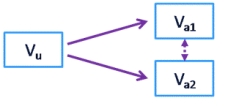
Wenn eine dritte, in der Analyse nicht berücksichtigte Variable die Ursache oder Verstärkung des miteinander Variierens von zwei Variablen ist, so nennt man dies eine Scheinkorrelation.
Wenn zwei Phänomene (Va1; Va2) immer gemeinsam auftreten, kann man fälschlich annehmen, sie hätten miteinander zu tun. In Wirklichkeit treten im Zusammenhang mit derselben unabhängigen Variablen (Vu) auf.
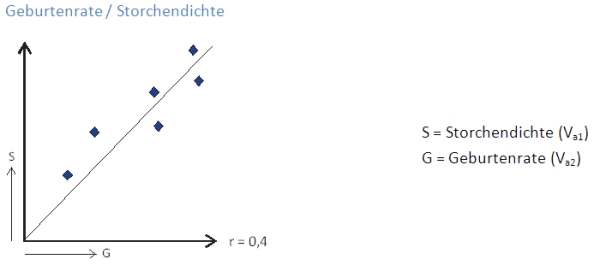
Beispiel Storchendichte:
Im Volksmund existiert der Glaube, dass Störche Kinder bringen. Überprüfen WissenschaftlerInnen diesen Volksglauben, so stellen sie fest, dass es ein gemeinsames Auftreten von Störchen und Geburten gibt.
Erhebt man Storchendichte (Va1) und Geburtenrate (Va2) von Kindern, so zeigt sich in den Berechnungen ein positiver Zusammenhang mit einem positiven Korrelationskoeffizienten.
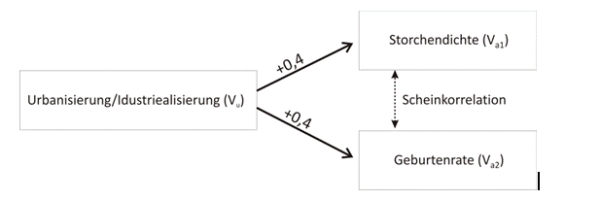
Sucht man eine Erklärung für dieses Phänomen, so muss man noch zusätzliche Faktoren berücksichtigen. Kontrolliert man die Umstände unter denen viele Störche / viele Geburten bzw. wenig Störche / wenig Geburten gefunden werden, so stellt man nach eingehender Überprüfung fest, dass mit steigender Urbanisierung und Industrialisierung sowohl die Geburten als auch die Storchendichte sinken - allerdings unabhängig voneinander. Den Störchen wird der Lebensraum entzogen und Frauen sind in Industriegesellschaften meist in außerhäuslicher Erwerbstätigkeit integriert und bekommen somit weniger Kinder.
Beide Phänomene (weniger Geburten und weniger Störche) werden, unabhängig voneinander, durch die Industrialisierung und Urbanisierung (Vu) beeinflusst. Es zeigt sich ein gleichzeitiger Effekt.
Nächstes Kapitel: 2.13 Methoden