Ausgewählte statistische Grundlagen und Analysemethoden/Eignung
Vorheriges Kapitel: 3. Ausgewählte statistische Grundlagen und Analysemethoden
Contents
- 1 3.1 Notwendiges Wissen für die Wahl geeigneter statistischer Analysemethoden
- 1.1 Analysemethoden sind abhängig von Datenart, -ausprägung, -anzahl und -verteilung:
- 1.2 Körpergrößen und Lieblingsobst
- 1.3 Inhalt
- 1.4 3.1.1 Arten von Messwerten (Daten)
- 1.5 3.1.2 Skalenniveaus
- 1.6 3.1.3 Verteilungen
- 1.6.1 3.1.3.1 Normalverteilung
- 1.6.2 3.1.3.2 Andere Verteilungsformen
- 1.6.3 3.1.3.3 Test auf Normalverteilung
- 1.6.4 3.1.3.3.1 Optischer Nachweis einer Normalverteilung: das Histogramm
- 1.6.5 3.1.3.3.2 Nachweis der Normalverteilung: Kolmogorov-Smirnov-Test
- 1.6.6 3.1.3.3.2.1 Kolmogorov-Smirnov-Test mit SPSS
3.1 Notwendiges Wissen für die Wahl geeigneter statistischer Analysemethoden
verfasst von Erwin Ebermann
Analysemethoden sind abhängig von Datenart, -ausprägung, -anzahl und -verteilung:
Die Statistik bietet eine Vielzahl von Verfahren, mit deren Hilfe man Aufschlüsse über Sachverhalte gewinnen kann. Die meisten Verfahren können jedoch nur verwendet werden, wenn bestimmte Bedingungen erfüllt sind. Die Auswahl der möglichen Verfahren hängt besonders ab von
- der Art der Daten und den damit zusammenhängenden Skalenniveaus[1]
- der Verteilung[2] der Ausprägungen einer Variable
- der Größe der Stichprobe[3]
- dem (Nicht-)Auftreten von sogenannten ’Ausreißern’ oder Extremdaten
Falls Verfahren außerhalb ihrer Anwendungsbedingungen verwendet werden, ist die Wahrscheinlichkeit groß, dass sinnleere oder falsche Aussagen erhalten werden.
Körpergrößen und Lieblingsobst
Wenn wir in einer Schulklasse die durchschnittliche Körpergröße der SchülerInnen ermitteln wollen, wäre das arithmetische Mittel[4] eine durchaus vernünftige Kennzahl. Wir zählen dazu alle Körpergrößen zusammen und dividieren die Summe durch die Anzahl der KlassenschülerInnen. Wenn wir hingegen ermitteln möchten, was diese Schulklasse als Lieblingsobst bevorzugt, wäre das arithmetische Mittel Schwachsinn. Wir kämen dann zu wenig sinnvollen Aussagen, dass die Klasse 0,17 Äpfel, 0,12 Orangen, 0,11 Bananen etc. als Lieblingsobst aufweist.
Dass im ersten Fall das arithmetische Mittel verwendet werden konnte, im zweiten Falle jedoch nicht, hängt mit den unterschiedlichen Skalenniveaus zusammen. So gehört die Körpergröße zur Proportionalskala[5], während das Lieblingsobst in eine Nominalskala[6] eingeordnet wird.
Verweise:
[1] Siehe Kapitel 3.1.2
[2] Siehe Kapitel 3.1.3
[3] Siehe Kapitel 2.1.1
[4] Siehe Kapitel 3.3.2
[5] Siehe Kapitel 3.1.2.5
[6] Siehe Kapitel 3.1.2.2
Inhalt
3.1 Notwendiges Wissen für die Wahl geeigneter statistischer Analysemethoden
3.1.1 Arten von Messwerten (Daten)
Statistisch unterscheidet man Daten
- in welcher Weise die Umsetzung in numerische Werte zur sinnvollen Ordnung und weiteren möglichen Erkenntnissen führt: metrische und nichtmetrische Variable;
- über die Abstufungen ihrer Ausprägungen: stetige und diskrete Variable
3.1.1.1 Metrische und nichtmetrische Variablen
Metrische und nichtmetrische Variablen
Prinzipiell können wir zwischen metrischen und nichtmetrischen Variablen unterscheiden. Als metrische Merkmale (auch quantitative genannt) bezeichnet man Merkmale, deren Ausprägungen sich mittels Zahlen darstellen lassen, wobei auch Rangunterschiede und Abstand sinnvoll interpretiert werden können. Als nichtmetrische Variablen werden dementsprechend alle anderen bezeichnet.
Beispiele:
Wir können somit z.B. Körpergrößen sinnvoll reihen (von klein nach groß mit beliebig feinen Abstufungen) und auch Größenunterschiede vernünftig interpretieren. Fragen wir hingegen nach dem Lieblingsobst, wird die Reihung der Ergebnisse willkürlich sein und meist alphabetisch erfolgen. Theoretisch könnte man jedem Obst einen Zahlenwert zuweisen, dieser wird jedoch nichts über den dahinterliegenden Wert aussagen, also zufällig mit diesem verbunden sein. Ränge, wie z.B. der Beliebteste, der Zweitbeliebteste, der Drittbeliebteste usw. lassen sich zwar sinnvoll reihen, ihre Abstände lassen sich aber nicht interpretieren. D.h. wir können nicht sagen, dass der Drittbeliebteste gegenüber dem Viertbeliebtesten den gleichen Abstand hat wie der Beliebteste gegenüber dem Zweitbeliebtesten. Daher sind sowohl Nominaldaten (wie das erwähnte Obst) wie auch Ordinaldaten nichtmetrisch.
3.1.1.2 Stetige und diskrete Variablen
Stetige und diskrete Variablen
Metrische Daten können ebenfalls wieder unterschieden werden, nämlich in
- stetige oder kontinuierliche, wenn sie jeden beliebigen Wert eines bestimmten Intervalls annehmen können (z.B. Körpergröße 175,33 cm, Temperatur); und
- diskrete, wenn sie nur endlich viele Werte annehmen können (z.B. Augenzahl beim Würfeln, Anzahl der Kinder)
3.1.2 Skalenniveaus
Skalenniveaus (von scala ital. ’Treppe’) sind eindimensionale Folgen von Positionen, die unterschiedliche Ausprägungen eines Merkmals anzeigen.
Jede Variable kann einer bestimmten Form von Skalierung zugeordnet werden. Nach der Möglichkeit, die Ausprägungen sinnvoll zu reihen und bestimmte mathematische Operationen durchzuführen, unterscheidet man zwischen vier verschiedenen Skalierungsniveaus: Nominalskalierung, Ordinalskalierung, Intervallskalierung und Proportionalskalierung.
Je nach Skalierungsniveau können sehr viele Analyseverfahren (wie bei der Proportionalskalierung) oder sehr wenige Verfahren (wie bei der Nominalskalierung) zur Auswertung eingesetzt werden. Daher ist die Wahl der Art der Daten und Skalenniveaus bereits bei der Forschungskonzeption zu berücksichtigen.
3.1.2.1 Skalierungsniveaus bildlich erklärt
Die technische Definition der Skalierungsniveaus hat den Nachteil, dass viele Menschen sich unter ihnen nichts vorstellen können. Machen wir es etwas anschaulicher und auch mit Treppen.
Stellen Sie sich vor, Tischler sehr unterschiedlicher Begabung und Erfahrung würden Stufen für eine Treppe bauen.
Nominalskala:
Wir hätten zuerst den Amateurtischler, welcher extrem ungleichförmige Stufen baut. Die eine Stufe ist links viel höher als rechts, die andere hinten höher als vorne. Keine einzige ist so gleichförmig, dass sie überall höher ist als alle anderen, keine einzige ist so gleichförmig, dass sie überall niedriger ist als alle anderen. Mit anderen Worten: wir können die Stufen beliebig hintereinander reihen. Wir finden keinen eindeutigen logischen und zwingenden Ansatz zur Reihung. Nehmen wir die Höhe links, würden wir die Stufe A vor der Stufe B vor der Stufe C reihen; nehmen wir die Höhe rechts, die Stufe B vor der Stufe C vor der Stufe A; nehmen wir die Höhe vorne etc.
Eine derartige Treppe, die sich beliebig zusammensetzen lässt und eigentlich gar keine Treppe ist, weil man auf ihr nicht höher steigen kann, würde der Nominalskala entsprechen: Was besitzt man: Äpfel, Birnen, ein Auto, einen Hund etc.
Ordinalskala:
Der Tischler wird nun etwas geschickter. Er schafft es, die Stufen jeweils unterschiedlich hoch zu machen und zwar überall. Die Stufe B ist 1,2x so hoch wie die Stufe A, die Stufe C doppelt so hoch wie die Stufe B, die Stufe D 3x so hoch wie die Stufe C, die Stufe E 1,3x so hoch wie die Stufe D. Es ist nicht vorauszusagen, um wieviel die nächsthöhere Stufe höher sein wird, aber man weiß, sie ist höher. Es ist ein beschwerlicher Aufstieg, aber es ist ein Aufstieg. Das würde einer Ordinalskala entsprechen. Ein Beispiel dafür wäre eine Notenskala. Man weiß zwar nicht, um wieviel besser ein Schüler mit einem Sehr Gut als ein Schüler mit einem Gut war, aber dass es einen Unterschied gegeben hat, erscheint klar zu sein (außer der Lehrer war bekannt subjektiv, was vorkommen soll).
Intervallskala:
Der Tischler wird noch geschickter. er schafft es sogar alle Stufen jeweils um 30 cm höher zu machen als die jeweils vorausgegangene. Man kann nun blind die Stufen hinaufgehen, weil man die Abstände kennt. Das Problem: Die Stiege steht auf einem Schiff, welches im Mittelmeer herumfährt. Ich weiss nun zwar, dass ich 30 cm höher steige, wenn ich eine Stufe hinaufschreite und 90, wenn ich drei Stufen hinaufschreite, aber ich kann nicht angeben, in welcher Höhe über dem Meeresboden ich mich befinde. Sind es 150 m, sind es 300? Dadurch kann ich auch nicht angeben, ob ich mich auf der übernächsten Stufe doppelt so hoch befinde wie jetzt. Ich kann zwar mit fixen Abständen rechnen, aber ich habe keinen absoluten Nullpunkt (wo es nicht mehr tiefer geht, wie zum Meeresboden) zum Vergleich und daher kann ich nicht angeben, um wieviel höher ich sein werde, wenn ich x Stufen höhersteige. Dies nennt man eine Intervallskala, die Stufen werden in gleichen Intervallen höher.
Ein Beispiel dafür wäre unsere Temperaturskala in Celsius, wo wir nicht vom absoluten Nullpunkt ausgehen (das wäre der Meeresboden oder - 273 Grad Celsius), sondern von einem willkürlichen (nämlich vom Schiffsboden aus oder 0 Grad). Daher ist die Aussage, 10 Grad ist 5 Grad wärmer als 5 Grad richtig, aber die Aussage falsch, dass es damit doppelt so warm ist, denn tatsächlich hätte ich ein Verhältnis von 283 Grad: 278 Grad (vom absoluten Nullpunkt aus gemessen).
Proportionalskala:
Wenn wir die gleiche Stiege wie bei der Intervallskala nun an Land bringen und sie auf festen Boden stellen, dann können wir von einer Proportionalskala sprechen. Endlich können wir, wenn wir uns auf der dritten Stufe befinden, nicht nur sagen, wir sind jetzt 60 cm höher als auf der ersten. Wir können auch endlich die Verhältnisse richtig interpretieren. Wir können nun auch korrekt angeben, dass wir uns jetzt auf der dritten Stufe dreimal so hoch wie auf der ersten Stufe befinden (mit dem festen Boden als absolutem Nullpunkt, unter den kein Abstieg möglich ist). Dies ist nun eine Proportionalskala. Ein Beispiel dafür wären Körpergrößen. Jemand, der 1,80 m groß ist, ist doppelt so groß wie jemand, der 90 cm groß ist.
3.1.2.2 Nominalskalierung
Bei der Nominalskalierung handelt es sich um eine Klassifizierung von Objekten, bei welcher keinerlei sinnvolle Rangreihung möglich ist, weshalb meist zur alphabetischen Reihung gegriffen wird. Größer und kleiner, mehr oder weniger wichtig, mehr oder weniger ausgeprägt kann nicht unterschieden werden. Jede Reihung ist gleich sinnvoll.
Beispiele für Nominalskalierungen wären Zeitungen, die man liest; das Obst, das man isst; das Geschlecht von ProbandInnen; die Farben von Kleidungsstücken etc.
3.1.2.3 Ordinalskalierung
Bei der Ordinal- oder Rangskalierung werden Gegenstände oder Sachverhalte miteinander verglichen und nur der Größe oder Intensität entsprechend gereiht. Eine Rangreihung ist möglich und sinnvoll, jedoch können die Abstände nicht interpretiert werden, d.h. der Abstand vom Zweit- zum Drittgrößten kann anders sein als vom Dritt- zum Viertgrößten.
Beispiele wären die Beliebtheit von SchülerInnen (hier kann ich diese eindeutig danach reihen), die Sympathie für Zuwanderer etc.
Schulnoten ordinal- oder intervallskaliert?
Schulnoten werden von vielen behandelt, wie wenn sie zur Intervallskalierung gehören würden, in welcher Abstände interpretiert werden können. Daher errechnen viele zur Beurteilung der Qualität einer Klasse das arithmetische Mittel von Noten, was man jedoch nur bei zumindest intervallskalierten Variablen machen sollte. Überlegen wir: Falls Schulnoten intervallskaliert wären, müsste der Abstand von einer Schulnote zur nächstbesseren/- schlechteren einem präzisen und stabilen Leistungsunterschied zwischen SchülerInnen entsprechen. Oft ’steht’ man jedoch zwischen zwei Noten, die PrüferIn muss sich dennoch für eine entscheiden. Auch wenn alle SchülerInnen einer extrem begabten Klasse eine sehr gute Arbeit abgeben, wird die PrüferIn dennoch meistens versuchen, zwischen ihnen durch unterschiedliche Noten zu differenzieren, um die Motivation und den anspornenden Wettbewerb hochzuhalten. Daher gibt es trotz des offiziellen objektiven Anspruchs von Schulnoten einen zu hohen subjektiven Einfluss, um sie als intervallskalierte Variablen behandeln zu können.
3.1.2.4 Intervallskalierung
Bei der Intervallskalierung nimmt man gleiche Abstände (Intervalle) zwischen benachbarten Ausprägungen an, aber einen nur relativen und keinen absoluten Nullpunkt. Es kann zwar der Abstand zwischen den Werten interpretiert werden, nicht aber das Verhältnis der Werte zueinander.
Ein Beispiel für eine Intervallskala ist z.B. die Temperatur in Celsius. Es wäre falsch, anzunehmen, dass 10 Grad doppelt so warm sind wie 5 Grad. Bezogen auf den absoluten Nullpunkt (- 273 Grad) wäre das Verhältnis zwischen 10 Grad und 5 Grad genau 268:263.
3.1.2.5 Proportionalskalierung
Bei der Verhältnis- oder Proportionalskalierung gibt es einen absoluten Nullpunkt. Sowohl der Abstand zweier Werte wie auch ihr Verhältnis zueinander können interpretiert werden. Ein Baum mit einer Höhe von 3,6 Metern ist doppelt so hoch wie ein Baum mit einer Höhe von 1,8 Metern.
Beispiele für diese Form der Skalierung wären z.B. Körpergrößen, der Vitamingehalt von Früchten; der Wassergehalt von Körpern oder die Entfernung von Orten.
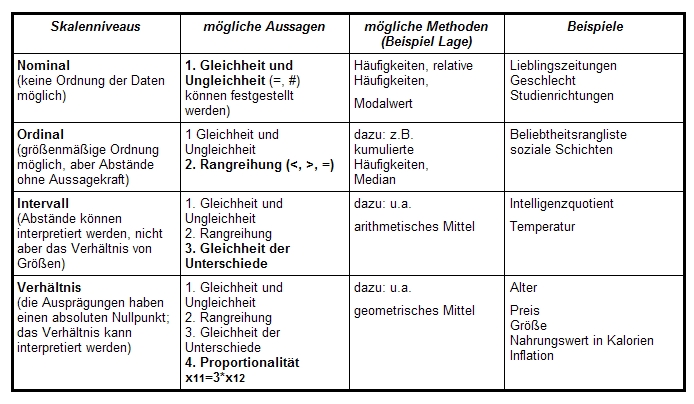
3.1.2.6 Skalierungstypen, Aussagen und Methoden
Die unterschiedlichen Skalierungsformen lassen unterschiedliche Analysemethoden zu:
Metrische Merkmale[1] finden sich bei Intervall- und Proportionalskalierung, nichtmetrische bei Nominal- und Ordinalskalierung.
Verweise:
[1] Siehe Kapitel 3.1.1.1
3.1.3 Verteilungen
(Häufigkeits-)Verteilungen geben Aufschluss über die Häufung aller Ausprägungen von Variablen. Man kann prinzipiell zwischen monovariablen und bivariablen Verteilungen unterscheiden.
Monovariable Verteilungen zeigen die Verteilung einer einzigen Variable, bei bivariablen Verteilungen werden die Häufigkeiten der einander entsprechenden Ausprägungen zweier Variablen aufgezählt, also z.B. 16 Personen sind sowohl weiblich wie auch Raucherinnen, 13 Personen männnlich und Nichtraucher.
Verteilungen können sowohl tabellarisch wie auch grafisch in Form von Diagrammen[1] dargestellt werden.
Zur tabellarischen Darstellung gelangt man, indem man die Werte (nach Möglichkeit sinnvoll) reiht und daneben die jeweilige Häufigkeit der Werte einträgt.
Zur grafischen Form gelangt man, wenn man in einem Diagramm auf der x- Achse die Ausprägung von Werten einträgt (z.B. die Körpergröße einer Person x) und auf der y- Achse deren Häufigkeit (= Zahl der Personen, welche genau diese Körpergröße aufweisen), dann können wir die Schnittpunkte mit Linien verbinden, wodurch sich eine Verteilungskurve ergibt. Die Standard- Darstellungsform dafür ist das Streudiagramm[2].
Verschiedene Verfahren erforden eine vorliegende Normalverteilung, die mit verschiedenen Prozeduren abschätzbar ist.
Verweise:
[1] Siehe Kapitel 3.6
[2] Siehe Kapitel 3.6.1.6
3.1.3.1 Normalverteilung
Von einer Normalverteilung sprechen wir, wenn
- die größte Häufigkeit in der Nähe des arithmetischen Mittel[1] auftritt und somit das arithmetische Mittel annähernd mit dem Median[2] und mit dem Modalwert[3] zusammenfällt;
- die Häufigkeiten[4] der Werte umso mehr abnehmen, je weiter sie sich vom Mittelwert entfernen;
- wenn sowohl links wie rechts des Mittelwerts eine prinzipielle Symmetrie vorliegt;
- wenn die Verteilungskurve glockenförmig ist.
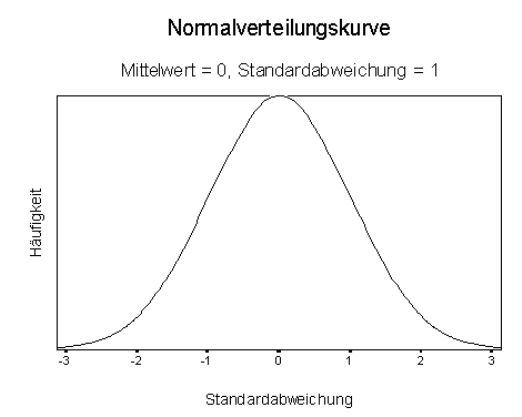
Eine Normalverteilung sieht wie in der folgenden Grafik aus:
Die im Diagramm verlaufende Kurve gibt die Häufigkeit der jeweiligen Werte an. Man sieht, dass die größten Häufigkeiten beim Mittelwert auftreten (0), die geringsten Häufigkeiten an den Extremen, wobei die Kurve glockenförmig verläuft (so genannte Gauß’sche Glockenkurve).
Dies wäre eine optimale Normalverteilung.
Verweise:
[1] Siehe Kapitel 3.3.2
[2] Siehe Kapitel 3.3.3
[3] Siehe Kapitel 3.3.1
[4] Siehe Kapitel 3.1.3.3.2
3.1.3.2 Andere Verteilungsformen
Neben der Normalverteilung können viele andere Verteilungsformen auftreten.
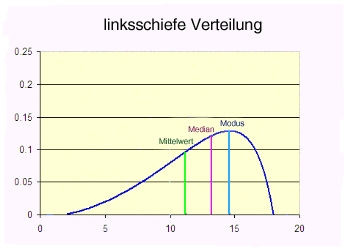
Oft sind die Verteilungen schief, man unterscheidet dann zwischen linksschiefen oder rechtsschiefen Verteilungen.
Bei der linksschiefen Verteilung (negative skew) liegt der höchste Punkt der Verteilung rechts (d.h. hier befindet sich der Großteil der Einträge), während nach links ein langgezogener Abfall eintritt (d.h. es treten dort selten verwendete Extremwerte auf). In linksschiefen Verteilungen ist der Median[1] größer als das arithmetische Mittel[2].
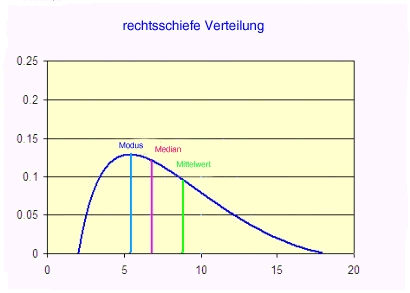
Bei der rechtsschiefen Verteilung (positive skew) finden wir die überwiegende Mehrzahl der Einträge auf der linken Seite und damit auch den höchsten Punkt der Kurve, während nach rechts wenige Einträge auftauchen. Typisch für eine derartige Verteilung ist die Einkommensverteilung sozial ungerechter Länder, in welchen wenigen MultimilliardärInneen viele KleinverdienerInnen gegenüberstehen. In rechtsschiefen Verteilungen ist der Median kleiner als das arithmetische Mittel.
Verteilungen können auch mehrere Gipfel aufweisen:
Diese Verteilung weist insgesamt zwei Gipfel auf. Sie wird als bimodal (zweigipfelig) bezeichnet.
Diese Verteilung ist rechteckig. Sie könnte bei einer kleinen Stichprobe[3] auftreten, wenn fast alle Werte die gleiche Häufigkeit[4] aufweisen.
Diese Verteilungsform ist u-förmig. Die Extremwerte kommen sehr häufig vor, während mittlere Ausprägungen fast nicht auftreten. Auch diese Verteilung ist bimodal.
Verweise:
[1] Siehe Kapitel 3.3.3
[2] Siehe Kapitel 3.3.2
[3] Siehe Kapitel 2.1.1
[4] Siehe Kapitel 3.1.3.3.2
3.1.3.3 Test auf Normalverteilung
Verschiedene Verfahren sind nur sinnvoll anwendbar, falls annähernd eine Normalverteilung der Daten vorliegt. Dazu gehört z.B. die Maßkorrelation[1], aber auch das arithmetische Mittel[2] ist nur wenig aussagekräftig, wenn die Verteilung[3] der Daten durch Ausreißer und extreme Schiefe geprägt sind.
Für den Nachweis einer Normalverteilung kann auf drei wesentliche Methoden zurückgegriffen werden:
- optisch: Für die optische Abschätzung der Normalverteilung kann auf die grafische Wiedergabe (siehe oben, mit Statistik- Programmen z.B. mit der grafischen Darstellung des Histogramms[4]) zurückgegriffen werden
- statistisch-mathematisch auf den Kolmogorov-Smirnov-Test (falls die Werte nicht in Klassen eingeteilt sind, besonders auch bei kleinen Stichproben)
- oder auf den Chi-Quadrat-Test (Wikipedia)[5] (bei in Klassen eingeteilten Daten)
Erkennung mit SPSS
Diese verschiedenen und als eigene Unterpunkte angeführten Untersuchungen können unter SPSS auch gleichzeitig getätigt werden. Klicken Sie dazu auf ANALYSIEREN -> DESKRIPTIVE STATISTIKEN -> EXPLORATIVE DATENANALYSE. Wählen Sie dort unter ’Anzeige’ die Alternative ’Beide’ und unter ’Diagramm’ die Alternative ’Normalverteilungsdiagramm mit Tests’. Dann wird in der Bildschirmausgabe der Resultate ein eigener Punkt aufgeführt: ’Tests auf Normalverteilung’, von denen uns besonders der erste der beiden Tests interessiert ’Kolmogorov-Smirnov’ (eigentlich eine verschärfte Variante dieses Tests). Liegt der Wert, welcher unter ’Signifikanz steht’, unter 0,05, so ist mit 95 % Sicherheit eine Normalverteilung zu verwerfen, liegt er unter 0,01, sogar mit 99 % Sicherheit.
Verweise:
[1] Siehe Kapitel 3.5.3.1
[2] Siehe Kapitel 3.3.2
[3] Siehe Kapitel 3.1.3
[4] Siehe Kapitel 3.6.1.5
[5] http://de.wikipedia.org/wiki/Chi-Quadrat-Test
3.1.3.3.1 Optischer Nachweis einer Normalverteilung: das Histogramm
Das Histogramm[1] liefert uns einen ersten und recht brauchbaren Eindruck, ob die von uns analysierten Daten weitgehend normalverteilt sind. Mit SPSS ist die Herstellung eines derartigen Diagramms ein Kinderspiel:
A. Klicken Sie in der Menüleiste auf GRAFIKEN
B. Wählen Sie Histogramm
C. Wählen Sie die zu untersuchende Variable aus
D. Lassen Sie sich am besten auch die Normalverteilungskurve zu Vergleichszwecken hinzeichnen (mit Häkchen markieren).
E. Klicken Sie auf OK
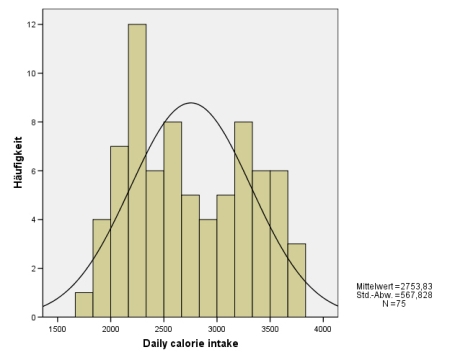
Dann erhalten Sie z.B. das folgende Histogramm (alle folgenden Histogramme und Analysen wurden von der SPSS-Datei world95.sav abgeleitet):
Hier ist z.B. eine stärkere Abweichung von der Normalverteilung gegeben. Man beachte den großen Zwischenraum zwischen der Normalverteilungskurve und den tatsächlichen Werten bei einem Kalorien-Input von etwa 3000. Dennoch wäre auf dem 5-%-Signifikanz-Niveau die Annahme einer Normalverteilung mit dem Kolmogorov-Smirnov-Test[2] noch nicht widerlegt (wohl aber auf dem 10-%-Niveau).
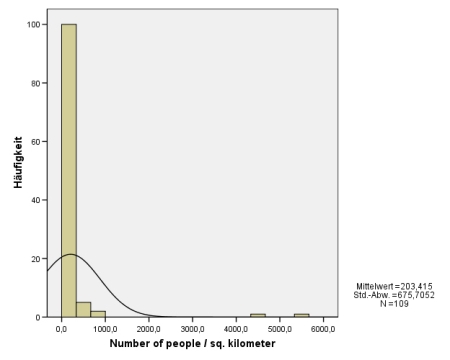
Das folgende Diagramm zeigt eine noch deutlich stärkere Abweichung von der Normalverteilung:
In diesem Fall ist auch der Kolmogorov-Smirnov-Test hochgradig signifikant (sowohl auf dem 5-% wie auch auf dem 1-%-Niveau), weshalb die Annahme einer Normalverteilung verworfen werden muss.
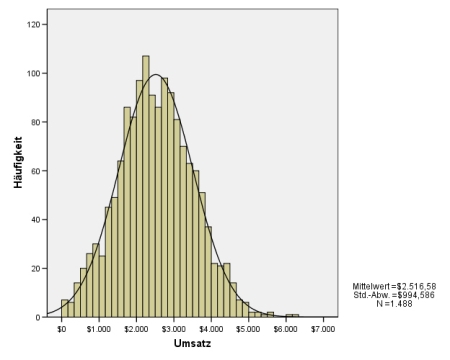
Deutlich normalverteilt, sowohl grafisch erkennbar wie auch mit dem Kolmogorov-Smirnov-Test nicht verwerfbar, ist die folgende Verteilung. Es finden sich kaum Zwischenräume zwischen der Normalverteilungskurve und der tatsächlichen Verteilung:
Man sieht, dass das Histogramm meist eine sehr gute Abschätzmöglichkeit erlaubt, ob Variable normalverteilt sind.
Verweise:
[1] Siehe Kapitel 3.6.1.5
[2] Siehe Kapitel 3.1.3.3.2
3.1.3.3.2 Nachweis der Normalverteilung: Kolmogorov-Smirnov-Test
Der Kolmogorov-Smirnov-Test kann auch bei kleineren Stichproben eingesetzt werden, um zu überprüfen, ob eine gegebene Verteilung mit hoher Wahrscheinlichkeit von der Normalverteilung abweicht.
Die Berechnung basiert auf dem Vergleich mit einer hypothetischen Normalverteilungskurve (Bild von Internet-Enzyklopädie Wikipedia: http://de.wikipedia.org/wiki/Kolmogorow-Smirnow-Test[1]):
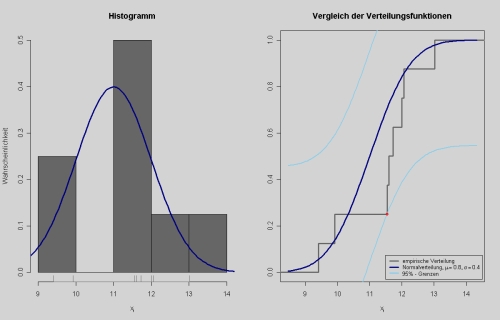
Die Logik der Berechnung geht davon aus, dass die tatsächliche Verteilung von einer hypothetischen Normalverteilung an einem beliebigen Punkt eine bestimmte flächenmäßige Abweichung nicht überschreiten darf, andernfalls müsste die Annahme einer Normalverteilung verworfen werden. Daher wird in einer Reihe von Rechenschritten die jeweilige konkrete Abweichung errechnet. Die größte auftretende Abweichung wird mit einer Tafel des Kolmogorov- Smirnov-Tests verglichen.
Ein Beispiel einer manuellen Berechnung kann hier eingesehen werden. Natürlich werden die Werte heute wesentlich komfortabler, z.B. mit SPSS, ermittelt.
Verweise:
[1] http://de.wikipedia.org/wiki/Kolmogorow-Smirnow-Test
3.1.3.3.2.1 Kolmogorov-Smirnov-Test mit SPSS
A. Sie wählen in SPSS den Menüpunkt ANALYSIEREN
B. Aus den heruntergeklappten Alternativen wählen Sie NICHTPARAMETRISCHE TESTS
C. Aus den nächsten Auswahlpunkten, die sich rechts öffnen, wählen Sie K-S BEI EINER STICHPROBE....
D. Nun wählen Sie die Testvariable aus, welche Sie auf Normalverteilung prüfen möchten. Achten Sie darauf, dass links unten unter Testverteilung der Punkt Normal angewählt ist.
E. Klicken Sie auf OK
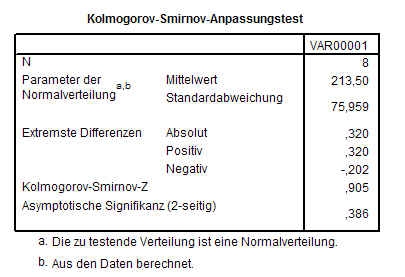
F. Sie erhalten nun eine Bildschirmausgabe wie folgende:
G. Hier sind für uns die folgenden Werte von Belang: 1. N (in diesem Falle 8), Extremste Differenzen 0,320) und Asymptotische Signifikanz.
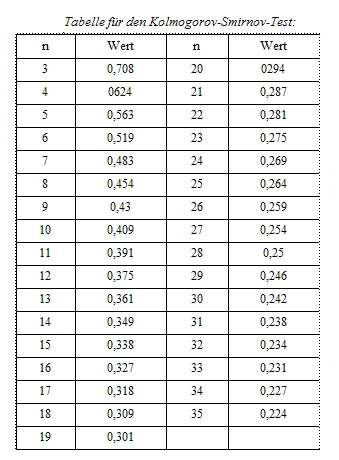
H. Nun vergleichen wir diese beiden ersten Werte mit einer Tabelle für den Kolmogorov-Smirnov-Test. Die nachfolgende Tabelle gibt bei einer 5 % Irrtumswahrscheinlichkeit Grenzwerte für Stichproben an, bei denen n zwischen 1-35 liegt.
Wir suchen nun den Wert für N = 8 und sehen dort die Zahl 0,454. Falls die Extremste Differenz in unserem Rechenbeispiel diesen Wert überschreitet, liegt mit 95 % Wahrscheinlichkeit keine Normalverteilung vor. In unserem Fall haben wir jedoch eine Extremste Differenz von nur 0,32. Das Ergebnis wird am Besten so interpretiert, dass die theoretische Annahme einer Standardverteilung nicht verworfen werden muss. Ein wirklicher Beweis für eine Standard- Verteilung liegt allerdings dadurch nicht vor.
Auch unser Wert für die Asymptotische Signifikanz ist weit größer als der Grenzwert 0,05. Dieser würde besagen, dass nur in 5 % aller Fälle eine derartige Verteilung wirklich normalverteilt ist. Ein Wert von 0,02 wäre hingegen deutlich kleiner, daher würde die Annahme einer Normalverteilung verworfen werden (auf dem 5 % Signifikanzniveau[1]). Da unser Wert jedoch deutlich darüber liegt, kann die Arbeitshypothese einer Normalverteilung auf diesem Signifikanzniveau nicht verworfen werden.
Achtung: Der Kolmogorov-Smirnov-Test benötigt, v.a. bei kleinen Stichproben, extreme Abweichungen von einer Normalverteilung, um auf höheren Signifikanzniveaus die Annahme einer Normalverteilung zu verwerfen. Daher ist eine Nichtverwerfung der Annahme einer Normalverteilung durch diese Berechnungsform noch kein Beweis für das Vorliegen einer Normalverteilung. Sollte sich im Histogramm[2] eine extreme Abweichung von der fakultativ gezogenen Normalverteilungskurve zeigen, dann sollte man, auch wenn der Kolmogorov-Smirnov-Test diese nicht verwirft, dennoch eher zu nicht parametrischen Tests greifen (wie z.B. dem T-Test etc.)
Hier ein Link zu weiterführenden Tabellen, in welchen noch weitere Irrtumswahrscheinlichkeiten für die Berechnung der Abweichung von einer Standardverteilung herangezogen werden: https://www.erieri.com/dlc[3]
Verweise:
[1] Siehe Kapitel 1.3.2
[2] Siehe Kapitel 3.6.1.5
[3] https://www.erieri.com/dlc/onlinetextbook/table7
Nächstes Kapitel: 3.2 Die Ermittlung von Häufigkeiten