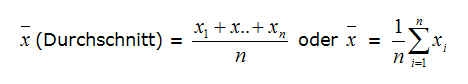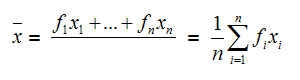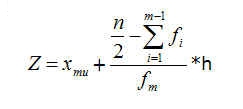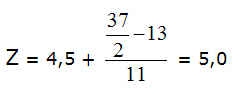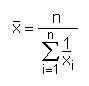Difference between revisions of "Ausgewählte statistische Grundlagen und Analysemethoden/Mittelwerte"
(Created page with " '''Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1 Notwendiges Wissen für die Wahl geeigneter statistischer Analysemethoden|Vorheriges Kapitel: 3.1 No...") |
m (Protected "Ausgewählte statistische Grundlagen und Analysemethoden/Mittelwerte" ([Edit=Allow only administrators] (indefinite) [Move=Allow only administrators] (indefinite)) [cascading]) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | '''[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Ermittlung#3.2 Die Ermittlung von Häufigkeiten|Vorheriges Kapitel: 3.2 Die Ermittlung von Häufigkeiten]]''' | |
| − | '''[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | + | = 3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz = |
| − | = 3. | ||
<sup>verfasst von Erwin Ebermann</sup> | <sup>verfasst von Erwin Ebermann</sup> | ||
| − | + | '''Lagemaße''' beschreiben das '''Zentrum einer Verteilung''' durch eine Kennzahl. | |
| − | + | Wenn wir von einem Land wissen, dass seine EinwohnerInnen durchschnittlich 2000 € monatlich verdienen, dann liefern uns Lagemaße eine erste ungenaue Idee, wo sich die EinwohnerInnen des Landes einkommensmäßig im Weltmaßstab einordnen lassen, sie ’liegen’ in der Gruppe der reicheren Länder. | |
| − | + | Lagemaße werden oft auch als '''Maßzahlen der zentralen Tendenz''' bezeichnet. Die am häufigsten benutzten Lagemaße sind das '''arithmetische Mittel''', das '''geometrische Mittel''', der '''Median''' und der '''Modalwert'''. | |
| − | * ''' | + | * Das '''arithmetische Mittel''' bezeichnet den Durchschnittswert aller Einträge, |
| − | * ''' | + | * das '''geometrische Mittel''' bezieht sich auf den Durchschnittswert voneinander abhängiger Werte (die sich also gegenseitig beeinflussen), |
| + | * der '''Median''' kennzeichnet die Normalität (welcher Wert befindet sich größenmäßig wirklich in der Mitte der Einträge und entspricht somit am ehesten dem ’Normalfall’), | ||
| + | * der '''Modalwert''' bezeichnet ausschließlich den am häufigsten vorkommenden Wert, der keinerlei Hinweis über die Eigenheiten der anderen Werte gibt. | ||
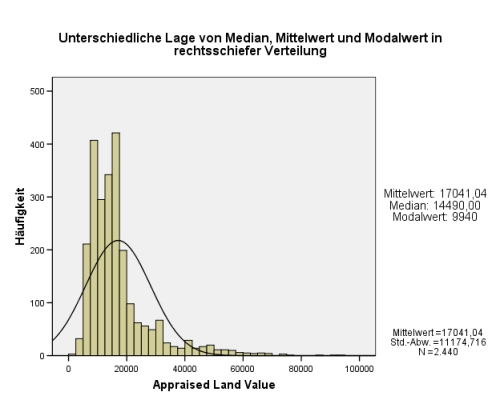
| − | + | Je nach '''Verteilung[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.3 Verteilungen|[1]]]''', '''Skalenniveau[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.2 Skalenniveaus|[2]]]''' und '''Art der Daten[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.1 Arten von Messwerten Daten|[3]]]''' sind unterschiedliche '''Lagemaße''' sinnvoll. Bei gegebener '''Normalverteilung[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.3.1 Normalverteilung|[4]9]''' stimmen sowohl '''Median''' wie auch der '''Modalwert''' mit dem '''Arithmetischen Mittel''' überein. In schiefen Verteilungen hingegen nehmen sie sehr unterschiedliche Positionen ein. In rechtsschiefen Verteilungen (der Abfall erfolgt nach rechts) ist der Modalwert am kleinsten, danach kommt der Median, am größten ist der Mittelwert. In '''linksschiefen Verteilungen''' ist es umgekehrt. | |
| − | |||
| − | |||
| + | [[File:quantitative-71_1.jpg|frame|center|Unterschiedliche Lage von Median, Mittelwert und Modalwert in rechtsschiefer Verteilung]] | ||
'''Verweise:'''<br /> | '''Verweise:'''<br /> | ||
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.2 Skalenniveaus|[ | + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.3 Verteilungen|[1] Siehe Kapitel 3.1.3]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1. | + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.2 Skalenniveaus|[2] Siehe Kapitel 3.1.2]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.1 Arten von Messwerten Daten|[3] Siehe Kapitel 3.1.1]]<br /> |
| + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.3.1 Normalverteilung|[4] Siehe Kapitel 3.1.3.1]]<br /> | ||
| − | == | + | ==Inhaltsverzeichnis== |
<div class="eksa_toc"> | <div class="eksa_toc"> | ||
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz|3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3.1 Modalwert|3.3.1 Modalwert]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3.2 Arithmetisches Mittel|3.3.2 Arithmetisches Mittel]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3.3 Median|3.3.3 Median]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | + | ::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3.3.1 Median bei gruppierten Daten|3.3.3.1 Median bei gruppierten Daten]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3.4 Geometrisches Mittel|3.3.4 Geometrisches Mittel]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3.5 Harmonisches Mittel|3.3.5 Harmonisches Mittel]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | + | ::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3.5.1 Harmonisches Mittel mit SPSS|3.3.5.1 Harmonisches Mittel mit SPSS]]<br /> |
| + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3.6 Wann welche Lagemaße?|3.3.6 Wann welche Lagemaße?]]<br /> | ||
| + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3.7 Berechnung von Lagemaßen mit SPSS|3.3.7 Berechnung von Lagemaßen mit SPSS]]<br /> | ||
</div> | </div> | ||
| − | == 3.2. | + | == 3.3.1 Modalwert == |
| + | |||
| + | Unter einem '''Modalwert''' versteht man '''die am häufigsten vorkommende Ausprägung''' einer Variable. | ||
| + | |||
| + | '''Beispiel:'''<br /> | ||
| + | In der folgenden geordneten Zahlenreihe 2, 3, 3, 3, 4, 4, 5, 6, 7 wäre ''3'' der Modalwert (weil diese Zahl dreimal auftritt, häufiger als jede andere Zahl). | ||
| + | |||
| + | ==== '''Mittelung bei benachbarten gleichgroßen Werten''' ==== | ||
| + | |||
| + | Falls mehrere benachbarte Werte die größte Häufigkeit aufweisen, so wird ihr '''arithmetisches Mittel''' berechnet. Haben z.B. die Werte 5 und 6 gleichermaßen die größte Häufigkeit, so ist der Modalwert der Durchschnitt dieser beiden Werte. | ||
| − | + | '''Beispiel:'''<br /> | |
| + | In der Zahlenreihe 2, 3, 3, 3, 4, 4, 4, 5, 6, 7 liegt der Modalwert bei 3,5. Sowohl ''3'' wie auch ''4'' kommen mit jeweilig dreimaligem Auftreten häufiger als die anderen Werte vor. Das arithmetische Mittel von ''3'' und ''4'' liegt bei 3,5. | ||
| − | + | ==== '''Modalklasse: Klasse mit größter Zahl an Einträgen''' ==== | |
| − | ''' | + | Bei '''klassierten Daten[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Ermittlung#3.2.3 Klassenbildung Gruppierung von Daten|[1]]]''' ist die '''Modalklasse''' diejenige Klasse mit der größten Zahl an Einträgen |
| − | + | ==== '''Nur selten praktische Relevanz des Modalwerts''' ==== | |
| − | + | Der '''Modalwert''' ist aussagekräftig, wenn ein einzelner Wert sehr häufig vorkommt (z.B. 27 '''Frauen''' und drei Männer) und unsinnig, wenn der häufigste Wert nur relativ selten vorkommt. Der '''Modalwert''' kann im Gegensatz zum '''arithmetischen Mittelwert''' oder zum '''Median''' auch sinnvoll in '''Nominalskalen[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.2.2 Nominalskalierung|[2]]]''' verwendet werden. | |
| − | |||
| − | |||
| − | + | '''Verweise:'''<br /> | |
| + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Ermittlung#3.2.3 Klassenbildung Gruppierung von Daten|[1] Siehe Kapitel 3.2.3]]<br /> | ||
| + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.2.2 Nominalskalierung|[2] Siehe Kapitel 3.1.2.2]]<br /> | ||
| + | |||
| + | == 3.3.2 Arithmetisches Mittel == | ||
| − | + | Das '''arithmetische Mittel''' ist die Summe aller Messwerte geteilt durch deren Anzahl: | |
| − | + | [[File:quantitative-73_1.jpg|frame|center|Formel für das arithmetische Mittel]] | |
| − | + | Z.B. die durchschnittliche Zahl von Schafen der Bauern im Dorf Nkorongoji in Mali: Die Messwerte sind: 5, 12, 3, 4, 7, 6. Die Summe ist 37, die Zahl der Messwerte ist 6, also ist das arithmetische Mittel 37/6= 6,17. | |
| − | ==== ''' | + | ==== '''Arithmetisches Mittel bei Einteilung der Messwerte in Klassen:''' ==== |
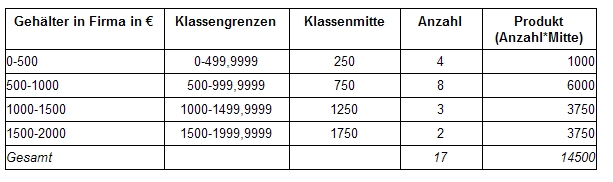
| − | Wenn | + | Wenn die Daten zahlreicher sind bzw. bereits in '''Klassen[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Ermittlung#3.2.3 Klassenbildung Gruppierung von Daten|[1]]]''' eingeteilt wurden, kann man das '''arithmetische Mittel''' einfacher berechnen: man multipliziert in jeder Klasse die '''Klassenmitte''' (Durchschnitt aus dem theoretisch kleinstem und größten Wert einer Klasse) mit der Zahl der Einträge in der jeweiligen Klasse: |
| − | + | [[File:quantitative-73_2.jpg|frame|center|Arithmetisches Mittel bei Einteilung der Messwerte in Klassen]] | |
| − | [[File:quantitative- | + | [[File:quantitative-73_3.jpg|frame|center|Beispiel für die Klassenmitte von Messwertklassen]] |
| − | + | ||
| − | + | Der Durchschnitt, in diesem Fall das durchschnittliche Gehalt, wäre somit 14500/17= 852,94. | |
| − | + | Das '''arithmetische Mittel''' stößt bei bestimmten Datenlagen jedoch auch auf einige Probleme. | |
| − | |||
| − | |||
| − | |||
| − | |||
'''Verweise:'''<br /> | '''Verweise:'''<br /> | ||
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Ermittlung#3.2.3 Klassenbildung Gruppierung von Daten|[1] Siehe Kapitel 3.2.3]]<br /> |
| + | |||
| + | == 3.3.3 Median == | ||
| − | + | Der '''Median''' ist jener Wert, welcher in einer größenmäßig geordneten Reihe '''genau in der Mitte''' liegt. D.h. oberhalb wie unterhalb von ihm befindet sich eine gleichgroße Anzahl von Einträgen. | |
| − | + | Warum benötigen wir ihn, da es doch auch das '''arithmetische Mittel[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3.2 Arithmetisches Mittel|[1]]]''' gibt? Das '''arithmetische Mittel''' ist der Mittelwert, der sich ergibt, wenn wir eine Summe durch die Anzahl der gezählten Elemente dividieren. | |
| − | + | ==== '''Beispiel: Verzerrung durch Mittel, nicht aber durch Median''' ==== | |
| − | + | Die folgende Grafik zeigt das individuelle Einkommen der EinwohnerInnen des fiktiven Ortes Largebread im Jahr 2002: | |
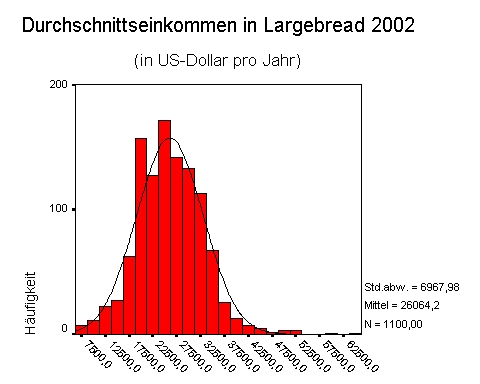
| − | + | [[File:quantitative-74_1.jpg|frame|center|Durchschnittseinkommen in Largebread]] | |
| − | + | Das durchschnittliche Einkommen von etwa 26000 $ scheint die Einkommenssituation der EinwohnerInnen von Largebread gut zu beschreiben. Die '''Normalverteilungskurve[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.3.3.1 Optischer Nachweis einer Normalverteilung: das Histogramm|[2]]]''' zeigt uns an, dass das Einkommen relativ gut normalverteilt ist. | |
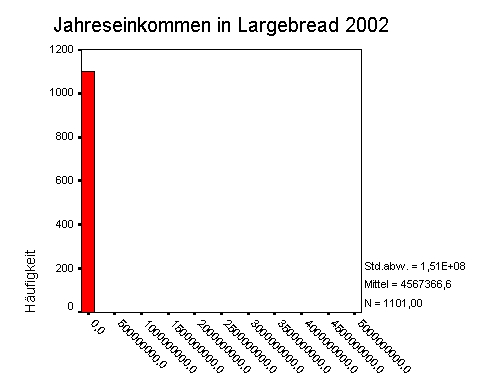
| − | + | Was würde aber jetzt passieren, wenn der reichste Mann der Welt, Bill Gates, sich plötzlich entschließen würde, nach Largebread zu ziehen? Bill Gates verfügt über ein Jahreseinkommen von 5 Milliarden $. Das Diagramm verändert sich extrem: | |
| − | [[File:quantitative- | + | [[File:quantitative-74_2.jpg|frame|center|Durchschnittseinkommen von Largebread mit Bill Gates]] |
| − | + | Haben ohne Bill Gates die 1100 EinwohnerInnen von Largebread durchschnittlich 26064 $ im Jahr verdient, so sind sie nun scheinbar über Nacht reich geworden und verdienen mit Bill Gate nun durchschnittlich fast 5 Millionen Dollar im Jahr. Man sieht deutlich, dass einzelne "Ausreißer" wie Bill Gates einen derartigen Durchschnittswert unsinnig machen können. Zur Beschreibung der Realität von Largebread ist daher ein Indikator für das durchschnittliche Einkommen deutlich besser geeignet, welcher Ausreißer nicht berücksichtigt, nämlich der Median: Das Durchschnittseinkommen in Largebread, berechnet nach dem Median, liegt ohne Bill Gates bei 26.000 und auch mit ihm nur bei 26.000 $. | |
| − | + | '''Probleme des Arithetischen Mittel:''' | |
| − | + | Das arithmetische Mittel stößt somit an seine Grenzen: | |
| + | * wo '''extreme Grenzwerte''' auftreten (wie in Largebread), | ||
| + | * '''bei sehr kleiner Beobachtungszahl''' (einzelne Werte können besonders leicht den Durchschnittswert verzerren), | ||
| + | * '''bei Verteilungen mit offenen Klassen''' (Schwierigkeit der Bestimmung der Klassenmitte der offenen Klassen), | ||
| + | * bei '''Ordinalskalen[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.2.3 Ordinalskalierung|[3]]]''' (hier sollte er nicht verwendet werden). | ||
| − | + | In all diesen Fällen ist es genauer, zum Median zu greifen. '''Der Median ist der Wert, der in einer geordneten Liste (oder primären Tafel) genau in der Mitte liegt, d.h. dass sich genauso viele Werte oberhalb wie unterhalb des Wertes befinden. Dieser Wert liegt an (n+1)/2ter Position.''' Hat man 3 Werte, dann ist der Medien der 2. Wert ([3+1]/2). | |
| − | + | '''Berechnung des Median bei Urliste:''' | |
| − | + | * Werte nach Größe rangreihen, | |
| + | * mittleren Wert nehmen, | ||
| + | * liegt der Median zwischen 2 Werten (wenn Median nicht ganze Zahl ist), dann wird der Durchschnitt der ihn umgebenden 2 Werte genommen. | ||
| − | + | z.B. Schulnoten 3,2,2,5,1,1,2,5 -> Rangreihung: 1,1,2,2,2,3,5,5 -> Der 4,5. Wert (Durchschnitt aus 2+2) ist der Median, also 2. | |
'''Verweise:'''<br /> | '''Verweise:'''<br /> | ||
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3.2 Arithmetisches Mittel|[1] Siehe Kapitel 3.3.2]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.3.3.1 Optischer Nachweis einer Normalverteilung: das Histogramm|[2] Siehe Kapitel 3.1.3.3.1]]<br /> |
| − | + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.2.3 Ordinalskalierung|[3] Siehe Kapitel 3.1.2.3]]<br /> | |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | ||
| − | + | ----- | |
| − | + | === 3.3.3.1 Median bei gruppierten Daten === | |
| − | ''' | + | Bei '''gruppierten Daten''' ist die Berechnung des '''Medians''' ein wenig komplizierter. Hier ist die rechnerische Abfolge: |
| − | |||
| − | + | * Bildung der '''Häufigkeitstabelle''' (inklusive kumulierter Häufigkeiten) | |
| + | * Ermittlung der Klasse ''m'', in welcher der '''Median''' steckt: wo liegt der Wert (n+1)/2. Diese wird nun als '''Medianklasse''' bezeichnet (n= Gesamtanzahl der Einträge) | ||
| + | * Ermittlung der unteren (=x<sup>mu</sup>) und oberen '''Klassengrenze''' (x) von ''m'' | ||
| + | * Ermittlung der '''Klassenbreite''' ''h'' (ergibt sich aus obere Klassengrenze - untere Kl.Grenze) . | ||
| + | * Subtraktion der akkumulierten Häufigkeit aller Klassen bis zur Klasse ''m'' (d.h. die Klassen 1 bis m-1) von n/2 -> Position des Medians in der Medianklasse | ||
| + | * Division der Position durch die Zahl der Werte der Klasse = relative Größenordnung des Medians (Anteile vom Ganzen der Klasse) | ||
| + | * Multiplikation des relativen Klassenanteils mit der Klassenbreite = absolute Größenordnung des Medians '''innerhalb''' der Klasse | ||
| + | * Addition der unteren Klassengrenze (in welcher der Median liegt) zur absoluten Größe des Medians (in der Klasse) = Endergebnis = Median ''Z'' | ||
| − | + | ||
| − | + | [[File:quantitative-75_1.jpg|frame|center|Formel für den Median bei gruppierten Daten]] | |
| − | + | ||
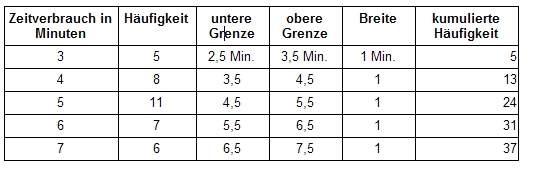
| − | + | '''Beispiel:''' Zeitverbrauch bei Lösung einer Aufgabe | |
| − | + | [[File:quantitative-75_2.jpg|frame|center|Beispiel - Tabelle für den Zeitverbrauch bei der Lösung einer Aufgabe]] | |
| + | n=37, Median ist also der 18. Wert, dieser liegt in der Klasse 5 (4,5-5,5 Minuten Dauer), daher: | ||
| + | [[File:quantitative-75_3.jpg|frame|center|Berechnung des Medians für das Beispiel "Zeitverbrauch"]] | ||
| − | + | Der Median liegt somit bei 5. | |
| − | |||
| − | |||
| + | == 3.3.4 Geometrisches Mittel == | ||
| − | -- | + | Das '''geometrische Mittel''' ist der '''Mittelwert bei mathematischen Produkten''', wie z.B. bei Wachstums- oder Zinsfaktoren. Das geometrische Mittel kann nur bei '''Proportionalskalen[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.2.5 Proportionalskalierung|[1]]]''' verwendet werden. Dieses wird als n- te Wurzel aus der relativen Veränderung (Endwert dividiert durch Anfangswert) berechnet, wobei n der Zahl der Zeiteinheiten entspricht. |
| − | + | '''Beispiel: durchschnittliche Inflationsrate'''<br /> | |
| + | Nehmen wir an, die jährliche Inflationsrate hätte durch 10 Jahre hindurch jeweils 2 % pro Jahr betragen. Hier wäre es falsch anzunehmen, dass die Inflation nach den 10 Jahren um 20 % höher als davor liegt, da sich die Werte gegenseitig beeinflussen. Im ersten Jahr sind es 2 % Inflation von 100 %; im 2. Jahr 2 % von 102 % (also 2,04 % Preissteigerung verglichen mit dem Ausgangsjahr), im 3. Jahr 2 von 104,04 (= 2,0808 % vergleichen mit dem Ausgangsjahr). | ||
| − | + | Ähnlich müssen wir zurückrechnen, wenn wir von einem bestimmten Preisniveau nach 10 Jahren auf die durchschnittliche Inflationsrate dieser 10 Jahre schließen wollen. | |
| − | + | ==== '''Errechnung der durchschnittlichen Inflationsrate''' ==== | |
| − | + | Der Lebenshaltungskostenindex liegt 2006 bei 136,5, vor 10 Jahren lag dieser bei 100. Somit erfolgte eine Preissteigerung von 36,5 % im Laufe der letzten 10 Jahre. Es wäre hier falsch, als durchschnittliche Preissteigerung/Jahr den Wert 3,65 % anzunehmen (36,5 % durch die Zahl der Jahre, also 10, dividiert), da sich die Werte gegenseitig beeinflussten (multiplizierten). | |
| − | + | Den richtigen Wert erhält man, wenn man die 10. Wurzel (da 10 Jahre) aus dem Gesamtveränderungsfaktor zieht. Diesen erhält man, indem man den Endwert durch den Ausgangswert dividiert: 136,5 dividiert durch 100 ist 1,365. Die 10.Wurzel daraus ist 1,0304. 100 multipliziert mit 1,024*1,0304*1,0304 etc. (insgesamt 10x damit multipliziert) ergibt nach 10 Jahren 136,5. | |
| − | + | Die Differenz zu 1 multipliziert mit 100 (es handelt sich ja um Prozente, bisher sind es nur Teile vom Ganzen) ist 0,0304*100 = 3,04 % jährliche Preissteigerung (und nicht 3,65, wenn wir das rein arithmetische Mittel genommen hätten). | |
| − | |||
| − | |||
| − | + | '''Verweise:'''<br /> | |
| + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.2.5 Proportionalskalierung|[1] Siehe Kapitel 3.1.2.5]]<br /> | ||
| − | |||
| − | + | == 3.3.5 Harmonisches Mittel == | |
| − | + | Das '''harmonische Mittel''' ist ein geeignetes Lagemaß für Größen, die durch einen '''(relativen) Bezug auf eine Einheit''' definiert sind: z.B. Geschwindigkeiten (Strecke pro Zeiteinheit) oder Ernteerträge (Gewicht oder Volumen pro Flächeneinheit). | |
| − | + | Die zur Berechnung benötigte Formel ist: | |
| − | + | [[File:quantitative-77_1.jpg|frame|center|Formel für die Berechnung des harmonischen Mittels]] | |
| − | + | '''Beispiel: Durchschnittsreisegeschwindigkeit'''<br /> | |
| + | Elke fährt von Wien nach Melk (etwa 100 km) mit einer Durchschnittsgeschwindigkeit von 80 km/h. Anschließend fährt sie mit durchschnittlich 120 km/h von Melk nach Linz und legt dabei ebenfalls 100 km zurück. Wie schnell fuhr sie im Schnitt? | ||
| + | Die meisten Befragten würden nach kurzer Überlegung 100 km/h als Durchschnittsgeschwindigkeit angeben. Doch ist dies falsch, da Elke unterschiedlich lange mit diesen beiden Geschwindigkeiten unterwegs war. Elke braucht für die ersten 100 km, die sie mit 80 km/h zurücklegt, insgesamt 100/80 Stunden, also 1,25 Stunden oder 1 Stunde und 15 Minuten. Für die zweiten Hundert Kilometer, die sie mit 120 km/h zurücklegt, benötigt sie 100/120 Stunden, also 5/6 Stunden oder 50 Minuten. Insgesamt legte sie somit 200 km in einer Zeit von 2,083 Stunden zurück (2 Stunden und 5 Minuten). 200 km dividiert durch die Zeit, die sie dafür benötigte, ergibt nun eine Durchschnittsgeschwindigkeit von 96,02 km/h. | ||
| − | + | ----- | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | == 3. | + | === 3.3.5.1 Harmonisches Mittel mit SPSS === |
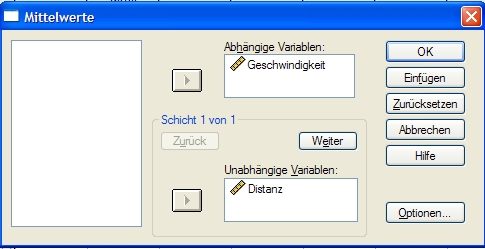
| − | + | Legen Sie zwei Variable an.Variable 1 für die Distanz, Variable 2 für die Geschwindigkeit. Nach Eingabe der Werte klicken Sie auf ANALYSIEREN - MITTELWERTE VERGLEICHEN - MITTELWERTE und geben dort unter ''Abhängige Variable'' die Geschwindigkeit ein, unter ''Unabhängige Variable'' die Distanz. | |
| − | + | [[File:quantitative-78_1.jpg|frame|center|Berechnung des harmonischen Mittels mit SPSS]] | |
| − | Sie | + | Klicken Sie dann auf ''Optionen'' und wählen Sie im nächsten Fenster das '''Harmonische Mittel''' aus. Fertig. |
| − | + | == 3.3.6 Wann welche Lagemaße? == | |
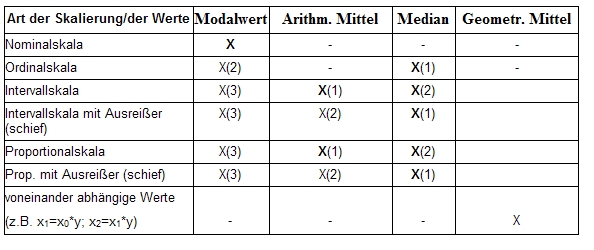
| − | [[File:quantitative- | + | [[File:quantitative-79_1.jpg|frame|center|Geeignetes Lagemaß bei verschiedenen Skalen]] |
| − | + | Die Zahl in Klammern gibt die Priorität an. X(1) wird daher als wichtiger als X(2) eingestuft. Fett markiertes X bezeichnet Kennzahlen, welche bei der gegebenen Datenart absolut sinnvoll sind, nicht fettes X liefert mögliche, aber nicht besonders sinnvolle oder teilweise sogar in die Irre führende Werte. | |
| − | + | Während Lagemaße bei '''eingipfeligen symmetrischen[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.3.1 Normalverteilung|[1]]]''' '''Daten''' weitgehend übereinstimmen und typisch für die Daten sind, sind sie bei '''anderen Verteilungsformen[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.3.2 Andere Verteilungsformen|[2]]]''' ('''U-förmige''', sehr '''schiefe''', '''mehrgipfelige''', '''gleichverteilte''') nicht aussagekräftig für die Verteilung. | |
| − | |||
| − | |||
| − | + | '''Verweise:'''<br /> | |
| + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.3.1 Normalverteilung|[1] Siehe Kapitel 3.1.3.1]]<br /> | ||
| + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.3.2 Andere Verteilungsformen|[2] Siehe Kapitel 3.1.3.2]]<br /> | ||
| − | |||
| − | + | == 3.3.7 Berechnung von Lagemaßen mit SPSS == | |
| − | + | Während das '''geometrische Mittel[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3.4 Geometrisches Mittel|[1]]]''' mit jedem mathematischen Taschenrechner leicht berechnet werden kann (einfach n-te Wurzel aus der Endzahl), sind die '''Lagemaße''' mit SPSS sehr einfach zu berechnen. | |
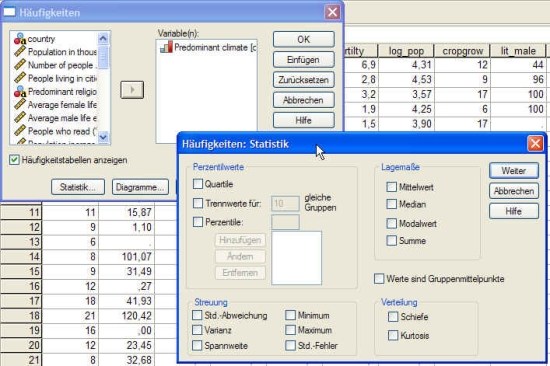
| − | + | Klicken Sie in der Menüleiste auf ANALYSIEREN - HÄUFIGKEITEN und wählen Sie dann ''Statistik'' aus: | |
| − | + | [[File:quantitative-80_1.jpg|frame|center|Berechnung von Lagemaßen mit SPSS]] | |
| − | + | Nun können Sie alle '''Lagemaße''' auswählen, den '''Mittelwert''', den '''Median''' und den '''Modalwert'''. Das folgende Resultat stammt aus der Berechnung der Lagemaße des Bruttonationalprodukts der Länder dieser Welt im Jahr 1995 (world95.sav). | |
| − | + | [[File:quantitative-80_2.gif|frame|center|Lagemaße des BNE aller Länder der Welt]] | |
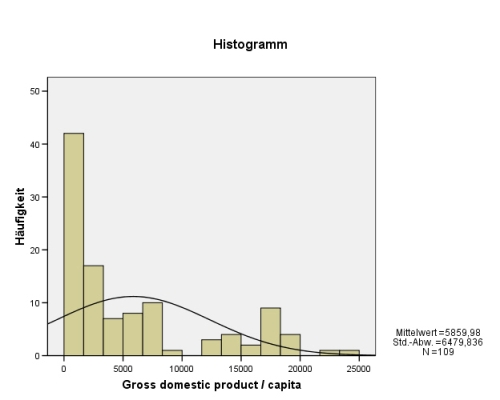
| − | + | Wir sehen, dass die '''Lagemaße''' extrem auseinanderliegen. Warum, macht das '''Histogramm[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Darstellung#3.6.1.5 Histogramme|[2]]]''' mit '''Normalverteilungskurve[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.3.1 Normalverteilung|[3]]]''' (anklicken unter ''Diagramme'') sofort sichtbar: Eine kleine Zahl von reichen Ländern hebt das '''arithmetische Mittel''' auf ein Niveau, welches außerhalb der Reichweite der meisten Länder dieser Welt liegt: | |
| − | [[File:quantitative- | + | [[File:quantitative-80_3.jpg|frame|center|Histogramm des BNE aller Länder der Welt]] |
| + | Wäre es eine '''Normalverteilung''', würden im Bereich (Artithm. Mittel +/s s) 68 % aller Werte liegen. Zieht man jedoch die Standardabweichung s (= 6479) vom Mittelwert ab, gelangt man am linken Rand bereits in den negativen Einkommensbereich. Auch dies zeigt die Sinnlosigkeit der Verwendung des '''arithmetischen Mittels''' bei diesen Daten. Der '''Median''' hingegen bildet hier die Realität mit knapp 3000 $ wesentlich besser ab. | ||
| + | |||
| + | |||
| + | '''Verweise:'''<br /> | ||
| + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3.4 Geometrisches Mittel|[1] Siehe Kapitel 3.3.4]]<br /> | ||
| + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Darstellung#3.6.1.5 Histogramme|[2] Siehe Kapitel 3.6.1.5]]<br /> | ||
| + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.3.1 Normalverteilung|[3] Siehe Kapitel 3.1.3.1]]<br /> | ||
<br /> | <br /> | ||
| − | '''[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/ | + | '''[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’|Nächstes Kapitel: 3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’]]''' |
---- | ---- | ||
| − | [[#3. | + | [[#3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz|↑ Nach oben]] |
Latest revision as of 14:32, 24 September 2020
Vorheriges Kapitel: 3.2 Die Ermittlung von Häufigkeiten
Contents
3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz
verfasst von Erwin Ebermann
Lagemaße beschreiben das Zentrum einer Verteilung durch eine Kennzahl.
Wenn wir von einem Land wissen, dass seine EinwohnerInnen durchschnittlich 2000 € monatlich verdienen, dann liefern uns Lagemaße eine erste ungenaue Idee, wo sich die EinwohnerInnen des Landes einkommensmäßig im Weltmaßstab einordnen lassen, sie ’liegen’ in der Gruppe der reicheren Länder.
Lagemaße werden oft auch als Maßzahlen der zentralen Tendenz bezeichnet. Die am häufigsten benutzten Lagemaße sind das arithmetische Mittel, das geometrische Mittel, der Median und der Modalwert.
- Das arithmetische Mittel bezeichnet den Durchschnittswert aller Einträge,
- das geometrische Mittel bezieht sich auf den Durchschnittswert voneinander abhängiger Werte (die sich also gegenseitig beeinflussen),
- der Median kennzeichnet die Normalität (welcher Wert befindet sich größenmäßig wirklich in der Mitte der Einträge und entspricht somit am ehesten dem ’Normalfall’),
- der Modalwert bezeichnet ausschließlich den am häufigsten vorkommenden Wert, der keinerlei Hinweis über die Eigenheiten der anderen Werte gibt.
Je nach Verteilung[1], Skalenniveau[2] und Art der Daten[3] sind unterschiedliche Lagemaße sinnvoll. Bei gegebener Normalverteilung[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.3.1 Normalverteilung|[4]9] stimmen sowohl Median wie auch der Modalwert mit dem Arithmetischen Mittel überein. In schiefen Verteilungen hingegen nehmen sie sehr unterschiedliche Positionen ein. In rechtsschiefen Verteilungen (der Abfall erfolgt nach rechts) ist der Modalwert am kleinsten, danach kommt der Median, am größten ist der Mittelwert. In linksschiefen Verteilungen ist es umgekehrt.
Verweise:
[1] Siehe Kapitel 3.1.3
[2] Siehe Kapitel 3.1.2
[3] Siehe Kapitel 3.1.1
[4] Siehe Kapitel 3.1.3.1
Inhaltsverzeichnis
3.3.1 Modalwert
Unter einem Modalwert versteht man die am häufigsten vorkommende Ausprägung einer Variable.
Beispiel:
In der folgenden geordneten Zahlenreihe 2, 3, 3, 3, 4, 4, 5, 6, 7 wäre 3 der Modalwert (weil diese Zahl dreimal auftritt, häufiger als jede andere Zahl).
Mittelung bei benachbarten gleichgroßen Werten
Falls mehrere benachbarte Werte die größte Häufigkeit aufweisen, so wird ihr arithmetisches Mittel berechnet. Haben z.B. die Werte 5 und 6 gleichermaßen die größte Häufigkeit, so ist der Modalwert der Durchschnitt dieser beiden Werte.
Beispiel:
In der Zahlenreihe 2, 3, 3, 3, 4, 4, 4, 5, 6, 7 liegt der Modalwert bei 3,5. Sowohl 3 wie auch 4 kommen mit jeweilig dreimaligem Auftreten häufiger als die anderen Werte vor. Das arithmetische Mittel von 3 und 4 liegt bei 3,5.
Modalklasse: Klasse mit größter Zahl an Einträgen
Bei klassierten Daten[1] ist die Modalklasse diejenige Klasse mit der größten Zahl an Einträgen
Nur selten praktische Relevanz des Modalwerts
Der Modalwert ist aussagekräftig, wenn ein einzelner Wert sehr häufig vorkommt (z.B. 27 Frauen und drei Männer) und unsinnig, wenn der häufigste Wert nur relativ selten vorkommt. Der Modalwert kann im Gegensatz zum arithmetischen Mittelwert oder zum Median auch sinnvoll in Nominalskalen[2] verwendet werden.
Verweise:
[1] Siehe Kapitel 3.2.3
[2] Siehe Kapitel 3.1.2.2
3.3.2 Arithmetisches Mittel
Das arithmetische Mittel ist die Summe aller Messwerte geteilt durch deren Anzahl:
Z.B. die durchschnittliche Zahl von Schafen der Bauern im Dorf Nkorongoji in Mali: Die Messwerte sind: 5, 12, 3, 4, 7, 6. Die Summe ist 37, die Zahl der Messwerte ist 6, also ist das arithmetische Mittel 37/6= 6,17.
Arithmetisches Mittel bei Einteilung der Messwerte in Klassen:
Wenn die Daten zahlreicher sind bzw. bereits in Klassen[1] eingeteilt wurden, kann man das arithmetische Mittel einfacher berechnen: man multipliziert in jeder Klasse die Klassenmitte (Durchschnitt aus dem theoretisch kleinstem und größten Wert einer Klasse) mit der Zahl der Einträge in der jeweiligen Klasse:
Der Durchschnitt, in diesem Fall das durchschnittliche Gehalt, wäre somit 14500/17= 852,94.
Das arithmetische Mittel stößt bei bestimmten Datenlagen jedoch auch auf einige Probleme.
Verweise:
[1] Siehe Kapitel 3.2.3
3.3.3 Median
Der Median ist jener Wert, welcher in einer größenmäßig geordneten Reihe genau in der Mitte liegt. D.h. oberhalb wie unterhalb von ihm befindet sich eine gleichgroße Anzahl von Einträgen.
Warum benötigen wir ihn, da es doch auch das arithmetische Mittel[1] gibt? Das arithmetische Mittel ist der Mittelwert, der sich ergibt, wenn wir eine Summe durch die Anzahl der gezählten Elemente dividieren.
Beispiel: Verzerrung durch Mittel, nicht aber durch Median
Die folgende Grafik zeigt das individuelle Einkommen der EinwohnerInnen des fiktiven Ortes Largebread im Jahr 2002:
Das durchschnittliche Einkommen von etwa 26000 $ scheint die Einkommenssituation der EinwohnerInnen von Largebread gut zu beschreiben. Die Normalverteilungskurve[2] zeigt uns an, dass das Einkommen relativ gut normalverteilt ist.
Was würde aber jetzt passieren, wenn der reichste Mann der Welt, Bill Gates, sich plötzlich entschließen würde, nach Largebread zu ziehen? Bill Gates verfügt über ein Jahreseinkommen von 5 Milliarden $. Das Diagramm verändert sich extrem:
Haben ohne Bill Gates die 1100 EinwohnerInnen von Largebread durchschnittlich 26064 $ im Jahr verdient, so sind sie nun scheinbar über Nacht reich geworden und verdienen mit Bill Gate nun durchschnittlich fast 5 Millionen Dollar im Jahr. Man sieht deutlich, dass einzelne "Ausreißer" wie Bill Gates einen derartigen Durchschnittswert unsinnig machen können. Zur Beschreibung der Realität von Largebread ist daher ein Indikator für das durchschnittliche Einkommen deutlich besser geeignet, welcher Ausreißer nicht berücksichtigt, nämlich der Median: Das Durchschnittseinkommen in Largebread, berechnet nach dem Median, liegt ohne Bill Gates bei 26.000 und auch mit ihm nur bei 26.000 $.
Probleme des Arithetischen Mittel:
Das arithmetische Mittel stößt somit an seine Grenzen:
- wo extreme Grenzwerte auftreten (wie in Largebread),
- bei sehr kleiner Beobachtungszahl (einzelne Werte können besonders leicht den Durchschnittswert verzerren),
- bei Verteilungen mit offenen Klassen (Schwierigkeit der Bestimmung der Klassenmitte der offenen Klassen),
- bei Ordinalskalen[3] (hier sollte er nicht verwendet werden).
In all diesen Fällen ist es genauer, zum Median zu greifen. Der Median ist der Wert, der in einer geordneten Liste (oder primären Tafel) genau in der Mitte liegt, d.h. dass sich genauso viele Werte oberhalb wie unterhalb des Wertes befinden. Dieser Wert liegt an (n+1)/2ter Position. Hat man 3 Werte, dann ist der Medien der 2. Wert ([3+1]/2).
Berechnung des Median bei Urliste:
- Werte nach Größe rangreihen,
- mittleren Wert nehmen,
- liegt der Median zwischen 2 Werten (wenn Median nicht ganze Zahl ist), dann wird der Durchschnitt der ihn umgebenden 2 Werte genommen.
z.B. Schulnoten 3,2,2,5,1,1,2,5 -> Rangreihung: 1,1,2,2,2,3,5,5 -> Der 4,5. Wert (Durchschnitt aus 2+2) ist der Median, also 2.
Verweise:
[1] Siehe Kapitel 3.3.2
[2] Siehe Kapitel 3.1.3.3.1
[3] Siehe Kapitel 3.1.2.3
3.3.3.1 Median bei gruppierten Daten
Bei gruppierten Daten ist die Berechnung des Medians ein wenig komplizierter. Hier ist die rechnerische Abfolge:
- Bildung der Häufigkeitstabelle (inklusive kumulierter Häufigkeiten)
- Ermittlung der Klasse m, in welcher der Median steckt: wo liegt der Wert (n+1)/2. Diese wird nun als Medianklasse bezeichnet (n= Gesamtanzahl der Einträge)
- Ermittlung der unteren (=xmu) und oberen Klassengrenze (x) von m
- Ermittlung der Klassenbreite h (ergibt sich aus obere Klassengrenze - untere Kl.Grenze) .
- Subtraktion der akkumulierten Häufigkeit aller Klassen bis zur Klasse m (d.h. die Klassen 1 bis m-1) von n/2 -> Position des Medians in der Medianklasse
- Division der Position durch die Zahl der Werte der Klasse = relative Größenordnung des Medians (Anteile vom Ganzen der Klasse)
- Multiplikation des relativen Klassenanteils mit der Klassenbreite = absolute Größenordnung des Medians innerhalb der Klasse
- Addition der unteren Klassengrenze (in welcher der Median liegt) zur absoluten Größe des Medians (in der Klasse) = Endergebnis = Median Z
Beispiel: Zeitverbrauch bei Lösung einer Aufgabe
n=37, Median ist also der 18. Wert, dieser liegt in der Klasse 5 (4,5-5,5 Minuten Dauer), daher:
Der Median liegt somit bei 5.
3.3.4 Geometrisches Mittel
Das geometrische Mittel ist der Mittelwert bei mathematischen Produkten, wie z.B. bei Wachstums- oder Zinsfaktoren. Das geometrische Mittel kann nur bei Proportionalskalen[1] verwendet werden. Dieses wird als n- te Wurzel aus der relativen Veränderung (Endwert dividiert durch Anfangswert) berechnet, wobei n der Zahl der Zeiteinheiten entspricht.
Beispiel: durchschnittliche Inflationsrate
Nehmen wir an, die jährliche Inflationsrate hätte durch 10 Jahre hindurch jeweils 2 % pro Jahr betragen. Hier wäre es falsch anzunehmen, dass die Inflation nach den 10 Jahren um 20 % höher als davor liegt, da sich die Werte gegenseitig beeinflussen. Im ersten Jahr sind es 2 % Inflation von 100 %; im 2. Jahr 2 % von 102 % (also 2,04 % Preissteigerung verglichen mit dem Ausgangsjahr), im 3. Jahr 2 von 104,04 (= 2,0808 % vergleichen mit dem Ausgangsjahr).
Ähnlich müssen wir zurückrechnen, wenn wir von einem bestimmten Preisniveau nach 10 Jahren auf die durchschnittliche Inflationsrate dieser 10 Jahre schließen wollen.
Errechnung der durchschnittlichen Inflationsrate
Der Lebenshaltungskostenindex liegt 2006 bei 136,5, vor 10 Jahren lag dieser bei 100. Somit erfolgte eine Preissteigerung von 36,5 % im Laufe der letzten 10 Jahre. Es wäre hier falsch, als durchschnittliche Preissteigerung/Jahr den Wert 3,65 % anzunehmen (36,5 % durch die Zahl der Jahre, also 10, dividiert), da sich die Werte gegenseitig beeinflussten (multiplizierten).
Den richtigen Wert erhält man, wenn man die 10. Wurzel (da 10 Jahre) aus dem Gesamtveränderungsfaktor zieht. Diesen erhält man, indem man den Endwert durch den Ausgangswert dividiert: 136,5 dividiert durch 100 ist 1,365. Die 10.Wurzel daraus ist 1,0304. 100 multipliziert mit 1,024*1,0304*1,0304 etc. (insgesamt 10x damit multipliziert) ergibt nach 10 Jahren 136,5.
Die Differenz zu 1 multipliziert mit 100 (es handelt sich ja um Prozente, bisher sind es nur Teile vom Ganzen) ist 0,0304*100 = 3,04 % jährliche Preissteigerung (und nicht 3,65, wenn wir das rein arithmetische Mittel genommen hätten).
Verweise:
[1] Siehe Kapitel 3.1.2.5
3.3.5 Harmonisches Mittel
Das harmonische Mittel ist ein geeignetes Lagemaß für Größen, die durch einen (relativen) Bezug auf eine Einheit definiert sind: z.B. Geschwindigkeiten (Strecke pro Zeiteinheit) oder Ernteerträge (Gewicht oder Volumen pro Flächeneinheit).
Die zur Berechnung benötigte Formel ist:
Beispiel: Durchschnittsreisegeschwindigkeit
Elke fährt von Wien nach Melk (etwa 100 km) mit einer Durchschnittsgeschwindigkeit von 80 km/h. Anschließend fährt sie mit durchschnittlich 120 km/h von Melk nach Linz und legt dabei ebenfalls 100 km zurück. Wie schnell fuhr sie im Schnitt?
Die meisten Befragten würden nach kurzer Überlegung 100 km/h als Durchschnittsgeschwindigkeit angeben. Doch ist dies falsch, da Elke unterschiedlich lange mit diesen beiden Geschwindigkeiten unterwegs war. Elke braucht für die ersten 100 km, die sie mit 80 km/h zurücklegt, insgesamt 100/80 Stunden, also 1,25 Stunden oder 1 Stunde und 15 Minuten. Für die zweiten Hundert Kilometer, die sie mit 120 km/h zurücklegt, benötigt sie 100/120 Stunden, also 5/6 Stunden oder 50 Minuten. Insgesamt legte sie somit 200 km in einer Zeit von 2,083 Stunden zurück (2 Stunden und 5 Minuten). 200 km dividiert durch die Zeit, die sie dafür benötigte, ergibt nun eine Durchschnittsgeschwindigkeit von 96,02 km/h.
3.3.5.1 Harmonisches Mittel mit SPSS
Legen Sie zwei Variable an.Variable 1 für die Distanz, Variable 2 für die Geschwindigkeit. Nach Eingabe der Werte klicken Sie auf ANALYSIEREN - MITTELWERTE VERGLEICHEN - MITTELWERTE und geben dort unter Abhängige Variable die Geschwindigkeit ein, unter Unabhängige Variable die Distanz.
Klicken Sie dann auf Optionen und wählen Sie im nächsten Fenster das Harmonische Mittel aus. Fertig.
3.3.6 Wann welche Lagemaße?
Die Zahl in Klammern gibt die Priorität an. X(1) wird daher als wichtiger als X(2) eingestuft. Fett markiertes X bezeichnet Kennzahlen, welche bei der gegebenen Datenart absolut sinnvoll sind, nicht fettes X liefert mögliche, aber nicht besonders sinnvolle oder teilweise sogar in die Irre führende Werte.
Während Lagemaße bei eingipfeligen symmetrischen[1] Daten weitgehend übereinstimmen und typisch für die Daten sind, sind sie bei anderen Verteilungsformen[2] (U-förmige, sehr schiefe, mehrgipfelige, gleichverteilte) nicht aussagekräftig für die Verteilung.
Verweise:
[1] Siehe Kapitel 3.1.3.1
[2] Siehe Kapitel 3.1.3.2
3.3.7 Berechnung von Lagemaßen mit SPSS
Während das geometrische Mittel[1] mit jedem mathematischen Taschenrechner leicht berechnet werden kann (einfach n-te Wurzel aus der Endzahl), sind die Lagemaße mit SPSS sehr einfach zu berechnen.
Klicken Sie in der Menüleiste auf ANALYSIEREN - HÄUFIGKEITEN und wählen Sie dann Statistik aus:
Nun können Sie alle Lagemaße auswählen, den Mittelwert, den Median und den Modalwert. Das folgende Resultat stammt aus der Berechnung der Lagemaße des Bruttonationalprodukts der Länder dieser Welt im Jahr 1995 (world95.sav).
Wir sehen, dass die Lagemaße extrem auseinanderliegen. Warum, macht das Histogramm[2] mit Normalverteilungskurve[3] (anklicken unter Diagramme) sofort sichtbar: Eine kleine Zahl von reichen Ländern hebt das arithmetische Mittel auf ein Niveau, welches außerhalb der Reichweite der meisten Länder dieser Welt liegt:
Wäre es eine Normalverteilung, würden im Bereich (Artithm. Mittel +/s s) 68 % aller Werte liegen. Zieht man jedoch die Standardabweichung s (= 6479) vom Mittelwert ab, gelangt man am linken Rand bereits in den negativen Einkommensbereich. Auch dies zeigt die Sinnlosigkeit der Verwendung des arithmetischen Mittels bei diesen Daten. Der Median hingegen bildet hier die Realität mit knapp 3000 $ wesentlich besser ab.
Verweise:
[1] Siehe Kapitel 3.3.4
[2] Siehe Kapitel 3.6.1.5
[3] Siehe Kapitel 3.1.3.1
Nächstes Kapitel: 3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’