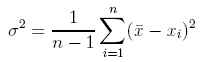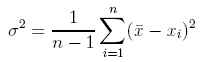Difference between revisions of "Ausgewählte statistische Grundlagen und Analysemethoden/Streuung"
(Created page with " '''Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz|Vorheriges Kapitel: 3.3 "Mittelwer...") |
m (Protected "Ausgewählte statistische Grundlagen und Analysemethoden/Streuung" ([Edit=Allow only administrators] (indefinite) [Move=Allow only administrators] (indefinite)) [cascading]) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
'''[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz|Vorheriges Kapitel: 3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz]]''' | '''[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz|Vorheriges Kapitel: 3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz]]''' | ||
= 3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’ = | = 3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’ = | ||
| Line 32: | Line 31: | ||
<div class="eksa_toc"> | <div class="eksa_toc"> | ||
[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’|3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’]]<br /> | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’|3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’]]<br /> | ||
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.1 Varianz|3.4.1 Varianz]]<br /> | + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.1 Varianz|3.4.1 Varianz]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.2 Standardabweichung|3.4.2 Standardabweichung]]<br /> | + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.2 Standardabweichung|3.4.2 Standardabweichung]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.3 Perzentile|3.4.3 Perzentile]]<br /> | + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.3 Perzentile|3.4.3 Perzentile]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.3.1 Quartile|3.4.3.1 Quartile]]<br /> | + | ::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.3.1 Quartile|3.4.3.1 Quartile]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.3.1.1 Die Ermittlung von Quartilen|3.4.3.1.1 Die Ermittlung von Quartilen]]<br /> | + | :::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.3.1.1 Die Ermittlung von Quartilen|3.4.3.1.1 Die Ermittlung von Quartilen]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.4 Berechnung von Streuungsmaßen mit SPSS|3.4.4 Berechnung von Streuungsmaßen mit SPSS]]<br /> | + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.4 Berechnung von Streuungsmaßen mit SPSS|3.4.4 Berechnung von Streuungsmaßen mit SPSS]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.5 Vergleichende grafische Darstellung von Streuung und Lage mit Box-Plots|3.4.5 Vergleichende grafische Darstellung von Streuung und Lage mit Box-Plots]]<br /> | + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.5 Vergleichende grafische Darstellung von Streuung und Lage mit Box-Plots|3.4.5 Vergleichende grafische Darstellung von Streuung und Lage mit Box-Plots]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.5.1 Erstellung von Boxplots mit SPSS|3.4.5.1 Erstellung von Boxplots mit SPSS]]<br /> | + | ::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4.5.1 Erstellung von Boxplots mit SPSS|3.4.5.1 Erstellung von Boxplots mit SPSS]]<br /> |
</div> | </div> | ||
| Line 199: | Line 198: | ||
[[File:quantitative-88_1.jpg|frame|center|Beispiel für Boxplots]] | [[File:quantitative-88_1.jpg|frame|center|Beispiel für Boxplots]] | ||
| − | |||
| − | |||
| − | |||
| Line 208: | Line 204: | ||
[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz|[2] Siehe Kapitel 3.3]]<br /> | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Mittelwerte#3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz|[2] Siehe Kapitel 3.3]]<br /> | ||
[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’|[3] Siehe Kapitel 3.4]]<br /> | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’|[3] Siehe Kapitel 3.4]]<br /> | ||
| − | |||
<br /> | <br /> | ||
Latest revision as of 14:32, 24 September 2020
Vorheriges Kapitel: 3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz
Contents
- 1 3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’
- 1.1 Grafische Darstellung der Streuung durch Histogramme
- 1.2 Lagemaße zeigen oft nur verzerrtes Bild der Realität bzw. Normalität
- 1.3 Inhalt
- 1.4 3.4.1 Varianz
- 1.5 3.4.2 Standardabweichung
- 1.6 3.4.3 Perzentile
- 1.7 3.4.4 Berechnung von Streuungsmaßen mit SPSS
- 1.8 3.4.5 Vergleichende grafische Darstellung von Streuung und Lage mit Box-Plots
3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’
verfasst von Erwin Ebermann
Streuungsmaße informieren über die Verteilung von Ausprägungen außerhalb des Zentrums. Sie liefern dadurch wertvolle Informationen über die (Un-)Ausgeglichenheit einer Verteilung.
Grafische Darstellung der Streuung durch Histogramme
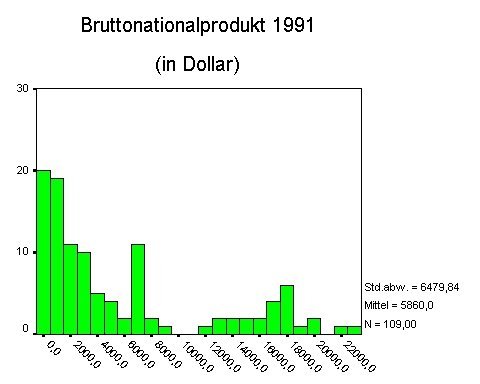
Histogramme[1] zeigen die relative "Gerechtigkeit" einer Verteilung in graphischer Form, wie z.B. das folgende über das Bruttonationalprodukt der Länder dieser Welt im Jahr 1991.
Dieses Histogramm zeigt optisch deutlich, dass im Jahr 1991 das durchschnittliche Bruttonationalprodukt von 5860 $ für die meisten Länder unerreichbar fern lag und damit keinerlei Aussagekraft für ihre Realität hatte. Der Median[2] lag damals bei der Hälfte des Mittelwerts[3], nämlich bei 2995 $. Ein Viertel der Länder wies ein Bruttonationalprodukt auf, welches unter 996 $ lag, ein Fünftel unter 681 $, ein Zehntel der Länder dieser Welt sogar unter 323 Dollar.
Lagemaße zeigen oft nur verzerrtes Bild der Realität bzw. Normalität
Man ersieht daraus, dass Kennzahlen wie das arithmetische Mittel[4] oft nur wenig geeignet sind, die Normalität darzustellen, d.h. dass der Wert des arithmetischen Mittel erheblich von der Realität der meisten Ausprägungen verschieden sein kann.
Wir benötigen daher weitere Kennzahlen, sogenannte Streuungsmaße, um Auskunft über die Randbereiche der Ausprägungen zu erhalten. Dazu zählen besonders die Standardabweichung und Perzentile bzw. Quartile[5].
Verweise:
[1] Siehe Kapitel 3.6.1.5
[2] Siehe Kapitel 3.3.3
[3] Siehe Kapitel 3.3.2
[4] Siehe Kapitel 3.3.2
[5] Siehe Kapitel 3.4.3.1
Inhalt
3.4.1 Varianz
Die Varianz ist eine Kennzahl, welche die Streuung aller Daten berücksichtigt. Sie wird berechnet, indem man den Durchschnitt der quadrierten Abweichung vom Arithmetischen Mittel[1] berechnet.
Je größer die Varianz verglichen mit dem Arithmetischen Mittel, desto stärker sind die Abweichungen der einzelnen Messwerte von diesem.
Ein Beispiel: Ein Arithmetisches Mittel von 100 kann sich ergeben, wenn alle Einträge der Zahl 100 entsprechen. Alle Einträge hätten dann eine Abweichung von 0 vom Arithmetischen Mittel, damit natürlich dann auch deren Quadrate sowie der Summen der Quadrate. Die Varianz wäre dann 0 und würde eine komplette Übereinstimmung aller Werte mit dem Arithmetischen Mittel anzeigen.
Ein Arithmetisches Mittel von 100 kann sich auch ergeben, wenn die Hälfte der Werte bei 0 und die andere Hälfte bei 200 liegt. In diesem Falle hätten wir eine extrem große Varianz (jeweils eine Abweichung von 100 vom Arithmetischen Mittel, diese wird quadriert, die Ergebnisse zusammengezählt und durch N dividiert. In diesem Falle erhielten wir eine Varianz von 10.000, Ausdruck der maximalen individuellen Abweichung der Meßwerte vom Arithmetischen Mittel.
In der Praxis verwendet man vor allem die Wurzel aus der Varianz, die sogenannte Standardabweichung[2].
Verweise:
[1] Siehe Kapitel 3.3.2
[2] Siehe Kapitel 3.4.2
3.4.2 Standardabweichung
Die Standardabweichung s gibt in einer Normalverteilung[1] einen Bereich um den Mittelwert[2] an, innerhalb dessen sich 68,2 % aller Einträge befinden. Innerhalb des Bereichs Mittelwert +/-2s befinden sich in einer Normalverteilung 95,44 % aller Einträge. Berechnet wird die Standardabweichung als Wurzel aus folgender Formel:
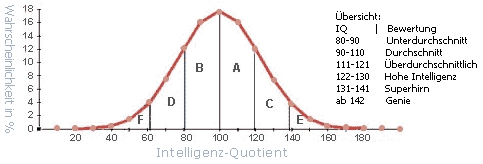
Beispiel: Intelligenzquotient (Durchschnitt = 100, s= 15).
Kenntnis der Standardabweichung = Kenntnis des Verlaufs der Verteilung
Auch wenn man die grafische Darstellung der Häufigkeitsverteilung, wie z.B. mit einem Histogramm[3], nicht kennt, kann man sie aufgrund der Kenntnis des Mittelwerts und der Standardabweichung weitgehend vorhersagen. Hat man einen Mittelwert von 100 und eine Standardabweichung von 10, wird die Verteilungskurve deutlich steiler sein, als wenn die Standardabweichung bei 30 liegt.
Kenntnis der Standardverteilung = Abschätzung der Häufigkeit von Ausprägungen
Die Kenntnis der Standardverteilung erlaubt uns, die Häufigkeit von Ausprägungen sofort einschätzen zu können. Wenn z.B. wie oben bekannt ist, dass der durchschnittliche Intelligenzquotient bei 100, die Standardabweichung bei 15 liegt, dann kann man sofort abschätzen, wie ein bestimmter Intelligenzquotient einzustufen ist. Wenn eine Person X einen IQ von 130 aufweist, dann liegt dieser beim Mittelwert +2 Standardabweichungen. Daher kann man sofort abschätzen, dass der betreffende IQ höher ist als 98 % aller Einträge.
Erklärung:
95,44 % aller Einträge befinden sich im Bereich Mittelwert ±2s, d.h. 4,56 % liegen außerhalb dieses Bereichs. In unserem Beispiel würden 95,44% aller Werte zwischen 70 und 130 liegen, Die restlichen 4,56 % teilen sich zu gleichen Teilen auf die darunter und darüber liegenden Bereiche auf. Somit bleiben für den Bereich ab 130 insgesamt 2,28 % aller Einträge übrig.
Verweise:
[1] Siehe Kapitel 3.1.3.1
[2] Siehe Kapitel 3.3.2
[3] Siehe Kapitel 3.6.1.5
3.4.3 Perzentile
Perzentile teilen die Ausprägungen der Variablen in gleich große Gruppen, sodass sich in jeder Gruppe der gleiche Prozentsatz an Einträgen befindet.
Besonders beliebt dabei sind die Quartile (= Viertel, jeweils 25 %). Bei Dezilen handelt es sich hingegen um Gruppen von jeweils 10 % der Werte.
3.4.3.1 Quartile
Quartile teilen die Verteilung in vier gleich große Viertel: 25 % der Werte sind kleiner oder gleich groß mit dem 1. Quartil, 50 % sind kleiner oder gleich groß wie das 2. Quartil (daher ist das 2. Quartil gleichzusetzen mit dem Median), 75 % sind kleiner oder gleich groß mit dem 3. Quartil. Quartile sollten erst ab einer Stichprobengröße[1] von zumindest 20 eingesetzt werden.
Verweise:
[1] Siehe Kapitel 2.1.1
3.4.3.1.1 Die Ermittlung von Quartilen
Die Ermittlung von Quartilen (gewichtet):
- man reiht die Werte nach ihrer Größe (unser Beispiel: Besitz von Büchern zur Ethnologie)
z.B. 1, 2, 3, 3, 5, 7, 11, 16, 17, 17, 20, 22, 25, 48, 52, 56, 76, 89, 96, 115
20 verschiedene Einträge liegen vor, daher ist n=20.
- Berechung des 1. Quartils, d.h. der Wert, welcher größer als 25 % und kleiner als 75 % aller Werte ist. Q1 liegt an der (n+1)/4. Stelle
Dieser Wert liegt in unserem Beispiel an der (n+1)/4 Stelle = 5.25, also zwischen dem 5. Wert (=5) und dem 6. Wert (=7). Der Bruchteil (0,25) gibt an, dass zum Wert von 5 noch ¼ des Abstands zwischen 5 und 6 hinzukommt. Q1 ist daher 5 + 0,25*2 = 5,5.
- Berechnung des 2. Quartils (wird berechnet wie der Median). Dieser liegt zwischen der 10. und 11. Stelle, daher ist der Wert zu mitteln (17+20)/2 = 18,5
- Berechnung des 3. Quartils, d.h. der Wert, welcher größer als 75 % und kleiner als 25 % der sortierten Werte ist. Q3 = 3*(n+1)/4
In unserem Beispiel: Q3 = 3*21/5 = 15,75. Stelle. Q3 liegt zwischen dem 15. Wert (= 52) und dem 16. Wert (= 56). Der Bruchteil (0,75) gibt an, dass zum 15. Wert noch ¾ des Abstands zwischen dem 15. und dem 16. Wert hinzukommen, daher: Q3 = 52 + 0,75*4 = 55.
Wir können nun die Aussage machen, dass Personen aus dem ersten oder untersten Quartil (Viertel) weniger als 5,5 Bücher, aus dem obersten Quartil hingegen mindestens 55 Bücher besitzen.
3.4.4 Berechnung von Streuungsmaßen mit SPSS
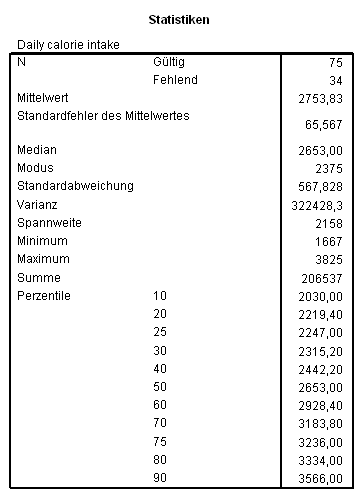
SPSS ermöglicht es, alle Arten von Streuungsmaßen mit wenigen Tastenklicks gleichzeitig zu berechnen.
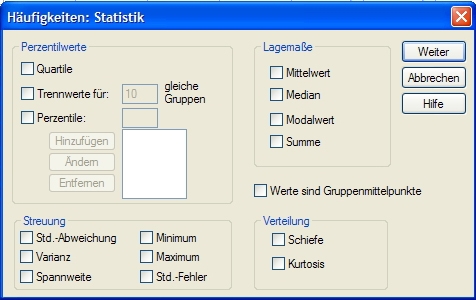
Dazu genügt es, auf ANALYSIEREN - DESKRIPTIVE STATISTIKEN - HÄUFIGKEITEN zu klicken, dann links unten nochmals auf Statistik zu klicken und im neuen Fenster alle nur denkbaren Kennzahlen für Lage- und Streuungsmaße anzuwählen:
Für die Berechnung von Quartilen[1] genügt das Setzen eines Häkchens in Quartile, möchte man Dezile (also in 10%-Gruppen) berechnen, gibt man im Feld Trennwerte für die Zahl 10 ein (dadurch werden 100 % auf 10 gleiche Gruppen aufgeteilt, also besteht jede Gruppe aus 10 %). Gibt man einen Wert X im Feld neben Perzentile ein und klickt auf Hinzufügen (wie z.B. die Zahl 37), so wird ermittelt, unterhalb welchen Kennwerts X % der Einträge liegen (in diesem Fall 37 %). Man kann beliebig viele dieser Perzentile setzen.
SPSS bietet die Berechnung und Darstellung von Streuungsmaßen in einer Vielzahl statistischer Verfahren an, meist unter einem Auswahlpunkt Statistik.
Verweise:
[1] Siehe Kapitel 3.4.3.1
3.4.5 Vergleichende grafische Darstellung von Streuung und Lage mit Box-Plots
Boxplots sind konzentrierte grafische Darstellungen von Lage und Streuung. Boxplots geben einen exzellenten optischen Überblick über wesentliche Parameter von Lage und Streuung, wie das Arithmetisches Mittel, die Quartile sowie über die Grenzwerte nach unten wie nach oben, wobei Ausreißer spezifisch markiert werden.
Informationen der Boxplots:
Boxplots enthalten eine Fülle von Hinweisen, wie im obigen Diagramm:
A. ein Kästchen, welches den Abstand zwischen dem 1. und dem 3. Quartil[1] markiert (Streuung)
B. eine langgezogene Linie, die von Extremwert zu Extremwert führt: Range (Streuung);
C. Einen Querstrich im Kästchen, welcher das Arithmetische Mittel[2] markiert;
D. Mit * bezeichnete Einträge, welche mehr als 3 Kästchenlängen entfernt liegen (Ausreißer).
E. Mit Kreis gekennzeichnete Einträge liegen 1,5-3 Kästchenlängen entfernt.
F. Neben diesen Ausreißern steht auch jeweils die Nummer des Datensatzes, in welchem diese Ausreißer gefunden werden können.
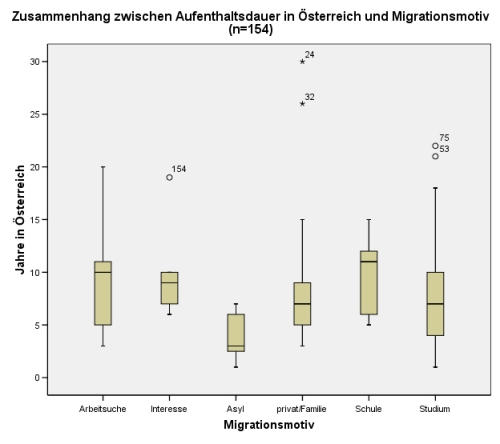
Extreme Informationsdichte durch Boxplots:
Durch diese konzentrierten Informationen erlauben Boxplots eine sehr schnelle Abschätzung sowohl der Lage wie auch der Streuung. Im obigen Boxplot, welches auf der y-Achse die Zahl der in Österreich verbrachten Jahre, auf der x-Achse das Migrationsmotiv widerspiegelt, kann man auf den ersten Blick ersehen, dass das Gros der AsylwerberInnen erst in den letzten Jahren kam, hingegen das Motiv Schulbesuch ein länger zurückliegender Migrationsgrund war. Die große Streuung (ausgedrückt durch die Länge des Kästchens) bei der Arbeitsuche gibt einen Hinweis darauf, dass viele Menschen über längere Zeit hinweg aus diesem Grund zuwanderten, während der Asylgrund einen wesentlich kürzeren Zeitraum betraf.
Verweise:
[1] Siehe Kapitel 3.4.3.1
[2] Siehe Kapitel 3.3.2
3.4.5.1 Erstellung von Boxplots mit SPSS
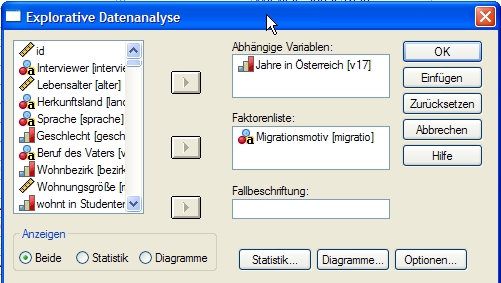
Klicken Sie in SPSS in der Menüleiste auf ANALYSIEREN - DESKRIPTIVE STATISTIKEN - EXPLORATIVE DATENANALYSE. Das folgende Fenster erscheint:
Sie finden links die Liste der Variablen. Übertragen Sie ins Feld Abhängige Variablen die Variable, deren Lage und Streuung Sie mittels eines Boxplots darstellen möchten. Beachten Sie bitte, dass es sich dabei zwingend um eine metrische Variable[1] handeln muss. Falls Sie die Lage[2] und Streuung[3] der gesamten Einträge dieser Variablen wiederspiegeln möchten, können Sie auf OK klicken. Das Boxplot erscheint in der Ausgabe nach einer Reihe statistischer Berechnungen.
Möchten Sie den Einfluss einer anderen Variable auf die gewählte Variable untersuchen, dann fügen Sie diese Variable in das Feld Faktorenliste ein. Sie erhalten dann verschiedene Boxplots, die jeweils Subgruppen der abhängigen Variablen bezeichnen:
Verweise:
[1] Siehe Kapitel 3.1.1.1
[2] Siehe Kapitel 3.3
[3] Siehe Kapitel 3.4
Nächstes Kapitel: 3.5 Der Zusammenhang zwischen Variablen