Difference between revisions of "Ausgewählte statistische Grundlagen und Analysemethoden/Darstellung"
(→Inhalt) |
m (Protected "Ausgewählte statistische Grundlagen und Analysemethoden/Darstellung" ([Edit=Allow only administrators] (indefinite) [Move=Allow only administrators] (indefinite)) [cascading]) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
'''[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5 Der Zusammenhang zwischen Variablen|Vorheriges Kapitel: 3.5 Der Zusammenhang zwischen Variablen]]''' | '''[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5 Der Zusammenhang zwischen Variablen|Vorheriges Kapitel: 3.5 Der Zusammenhang zwischen Variablen]]''' | ||
= 3.6 Die grafische Darstellung statistischer Ergebnisse = | = 3.6 Die grafische Darstellung statistischer Ergebnisse = | ||
| Line 280: | Line 278: | ||
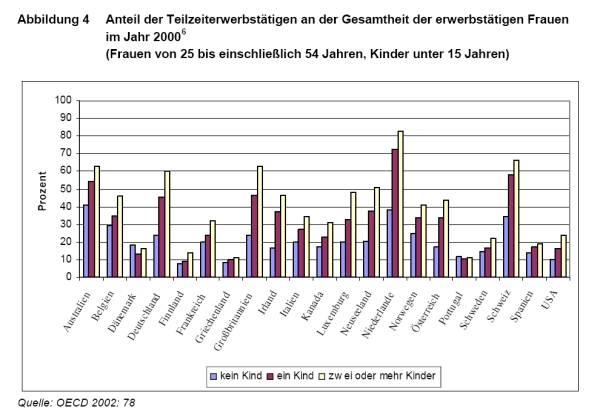
[[File:quantitative-124_1.jpg|frame|center|Gruppiertes Balkendiagramm Anteil der Teilzeiterwerbstätigen an der Gesamtheit der erwerbstätigen Frauen im Jahr 2000. Quelle: OECD 2002: 78.]] | [[File:quantitative-124_1.jpg|frame|center|Gruppiertes Balkendiagramm Anteil der Teilzeiterwerbstätigen an der Gesamtheit der erwerbstätigen Frauen im Jahr 2000. Quelle: OECD 2002: 78.]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 292: | Line 283: | ||
[http://www.mzes.uni-mannheim.de/publications/wp/wp-89.pdf [1] http://www.mzes.uni-mannheim.de/publications/wp/wp-89.pdf]<br /> | [http://www.mzes.uni-mannheim.de/publications/wp/wp-89.pdf [1] http://www.mzes.uni-mannheim.de/publications/wp/wp-89.pdf]<br /> | ||
| − | + | <br /> | |
'''[[Grundlagen_Statistischer_Auswertungsverfahren|↵ Zurück zur Übersicht]]''' | '''[[Grundlagen_Statistischer_Auswertungsverfahren|↵ Zurück zur Übersicht]]''' | ||
---- | ---- | ||
[[#3.6 Die grafische Darstellung statistischer Ergebnisse|↑ Nach oben]] | [[#3.6 Die grafische Darstellung statistischer Ergebnisse|↑ Nach oben]] | ||
Latest revision as of 14:32, 24 September 2020
Vorheriges Kapitel: 3.5 Der Zusammenhang zwischen Variablen
Contents
- 1 3.6 Die grafische Darstellung statistischer Ergebnisse
- 1.1 Ein Bild sagt mehr als 1000 Worte
- 1.2 Vorteil von Diagrammen liegt in Einfachheit der Darstellung
- 1.3 Nicht jedes Diagramm ist für jede Datenlage geeignet.
- 1.4 Begleitinformationen sind wichtig
- 1.5 Was in Diagrammen, was im Text?
- 1.6 Inhalt
- 1.7 3.6.1 Arten von Diagrammen
- 1.8 3.6.2 Welches Diagramm für welche Daten?
- 1.9 3.6.3 Notwendige Begleitinformationen von Diagrammen
3.6 Die grafische Darstellung statistischer Ergebnisse
verfasst von Erwin Ebermann
Ein Bild sagt mehr als 1000 Worte
Dies trifft auch für die Statistik zu. Wer es versteht, mit einfachen, klaren und aussagekräftigen Diagrammen zu punkten, wird für eine leichten und einprägsamen Zugang zu seinen Analysen Anerkennung finden.
Vorteil von Diagrammen liegt in Einfachheit der Darstellung
Allzuleicht lässt man sich von der Vielfalt an grafischen Darstellungsmöglichkeiten beeinflussen und meint, Diagramme noch ein wenig optisch ausgefaller, dreidimensional, vermeintlich attraktiver mit zahlreichen Schmankerln machen zu müssen, bis irgendwann einmal der Vorteil eines Diagramms gegenüber einer komplexen Tabelle verloren geht und die BetrachterInnen ratlos vor einem schwierig zu deutenden Kunstwerk sitzen. Niemand ist bereit, einige Minuten vor einem komplexen Diagramm zu sitzen, um zu versuchen, es zu verstehen. Mit Diagrammen gewinnt man die BetrachterIn in wenigen Sekunden oder man verliert sie/ihn. Die Notwendigkeit der inhaltlichen Klarheit und dadurch Schlichtheit eines Diagramms hat klare Priorität vor der künstlerischen Gestaltung.
Nicht jedes Diagramm ist für jede Datenlage geeignet.
Man sollte bedenken, dass nicht jedes Diagramm für jede Art von Information geeignet ist. Manche Diagramme, wie Kreisdiagramme[1], werden von den BetrachterInnen mit einem Ganzen, also 100 % assoziiert, und würden bei der Wiedergabe von Mehrfachantworten[2] zu falschen Schlüssen führen.
Begleitinformationen sind wichtig
Auch Diagramme benötigen Begleitinformationen, um sie voll verständlich zu machen und wissenschaftliche Seriösität nachzuweisen.
Was in Diagrammen, was im Text?
Zeigen Sie mit Diagrammen besondere Eigenheiten der Daten und packen Sie die Analysen und anderen notwendigen Begleitinformationen in den Text.
Verweise:
[1] Siehe Kapitel 3.6.1.1
[2] Siehe Kapitel 3.2.2
Inhalt
3.6.1 Arten von Diagrammen
Wesentliche Diagrammformen sind:
- Balkendiagramme, inklusive gruppierten Diagrammen und Stapelbalkendiagrammen
- Liniendiagramme
- Flächendiagramme
- Kreisdiagramme
- Boxplots[1]
- Streudiagramme
- Histogramme
- Kartogramme
Viele Programme ermöglichen die Erstellung von Diagrammen
Mit Ausnahme von Boxplots und Kartogrammen können alle Diagrammformen von den gängigen Programmen erstellt werden, wie sogar von WinWord (EINFÜGEN - GRAFIK - DIAGRAMM) oder Excel. In SPSS geht man in der Menüleiste zu GRAFIKEN und findet dort alle hier angeführten Diagrammformen und viele mehr zur Auswahl.
Auch hier gilt, dass professionelle statistische Programme wie z.B. SPSS oder Statistica Vorteile aufweisen, da sie eine Fülle feiner Einstellungen erlauben, welche mit Bordmitteln nicht zu erreichen sind. Auch verbinden sie in effizienter Form im gleichen Menüpunkt die gleichzeitige Berechnung und Erstellung komplexer Statistiken wie auch von Diagrammen.
Verweise:
[1] Siehe Kapitel 3.4.5.1
3.6.1.1 Kreisdiagramme
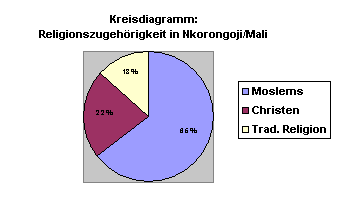
Kreisdiagramme (auch Tortendiagramme) genannt, sind eine beliebte grafische Darstellungsform, um die Aufteilung eines Ganzen aufzuzeigen.
Für die grafische Darstellung kategorieller Daten (Nominal[1]- oder Ordinalskalen[2]) verwendet man Diagrammformen, die eine möglichst klare Darstellung der relativen Anteile erlauben. Alle Anteile müssen zusammen 100 % ergeben. Der relative Anteil der einzelnen Bestandteile soll sofort optisch erkennbar sein. Damit diese relativen Anteile auf einem Blick größenmäßig eingeordnet werden können, dürfen nicht zu viele Kategorien verwendet werden. Sind sie zu zahlreich, sollten kleinere Kategorien nach Möglichkeit zusammengefasst werden. Andernfalls ist die Darstellung in Form einer Tabelle besser geeignet.
Besonders gut geeignet für die Darstellung relativer Anteile sind Torten- oder Kreisdiagramme:
Optimal große Teile, aber nicht zu viele.
Für das menschliche Auge sind Winkel von mehr als 90 Grad besonders gut zu erkennen. Deshalb eignen sich Tortendiagramme besonders zur Darstellung von Mehrheiten oder von Anteilen von mindestens einem Viertel.
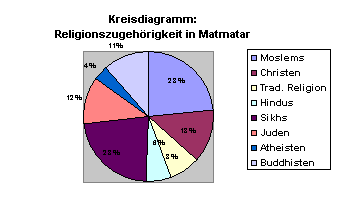
Wird die Anzahl der Anteile und damit der Tortenstücke zu zahlreich, wird ein Tortendiagramm schnell unübersichtlich, besonders wenn gleichzeitig seine größten Stücke kleiner als ein Viertel werden:
Hier ist es nur mehr mit Mühe möglich, die Tortenstücke nach ihrer Größe zu reihen, da die Rundung die Abschätzung der relativen Größe erschwert. Daher wären für die Darstellung vieler Subeinheiten eines Ganzen Stapelbalkendiagramme[3] besser geeignet.
Keinesfalls für Mehrfachantworten
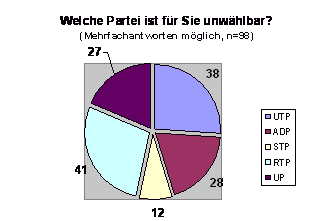
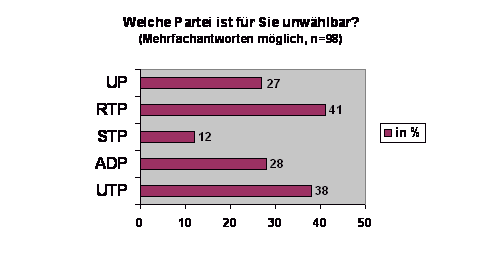
Gänzlich ungeeignet sind Kreisdiagramme, um die Ergebnisse von Fragen mit Mehrfachantworten darzustellen:
Bei Kreisdiagrammen neigen BetrachterInnen dazu, die gesamte Torte als etwas Ganzes, also als 100 % aufzufasssen.Da bei Mehrfachantworten jedoch mehr als 100 % auftreten können (auch weniger als 100 %), kann dies zu einer falschen Interpretation führen. Deutlich besser wären für diesen Zweck horizontale Balkendiagramme geeignet.
Verweise:
[1] Siehe Kapitel 3.1.2.2
[2] Siehe Kapitel 3.1.2.3
[3] Siehe Kapitel 3.6.1.3
3.6.1.2 Liniendiagramme
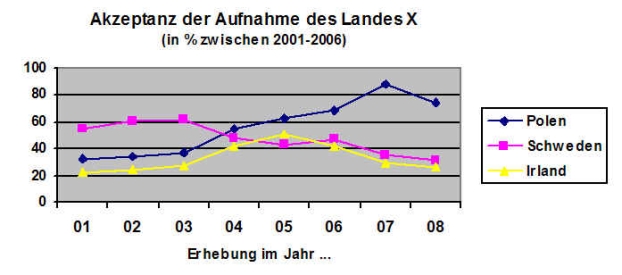
Liniendiagramme eignen sich besonders für die Darstellung von Entwicklungen, ganz besonders auch, wenn komparativ die Entwicklung von zwei oder mehr Populationen[1] miteinander verglichen wird. Durch die feinen Striche kann man auf engstem Raum Informationen gleich zu mehreren Untersuchungsobjekten unterbringen, wie man im folgenden fiktiven Beispiel sieht, in welchem gezeigt wird, wie sich in verschiedenen Ländern die Akzeptanz der Aufnahme eines weiteren Landes in die Europäische Union veränderte.
Man sieht auf einem Blick, dass in Schweden die Akzeptanz von einem hohen Niveau ausgehend stark zurückging, in Irland eher gering blieb, sich in Polen hingegen von einem sehr geringem zu einem relativ hohen Niveau entwickelte.
Verweise:
[1] Siehe Kapitel 2.1
3.6.1.3 Balkendiagramme
Einfache Balkendiagramme sind, da sie vom gleichen Nullpunkt ausgehen, sehr gut geeignet, um komparativ auch kleinste Unterschiede zwischen Subbereichen erkennbar zu machen.
Sie sind die beste Darstellungsform, um z.B. die Ergebnisse von Fragen mit Mehrfachantworten zu präsentieren.
Balkendiagramme können sowohl horizontal (wie das obige Beispiel) wie auch vertikal orientiert sein.
Das gruppierte Balkendiagramm
Dieses ist besonders geeignet für die kontrastive Darstellung der Ausprägungen einer Variable (z.B. männlich-weiblich für Geschlecht, Hinduismus-Islam etc. für Religionen). So kann man z.B. vergleichend zeigen, wie Männer und Frauen in verschiedenen Bereichen abschneiden. Siehe ein Beispiel dazu bei der Berechnung mit SPSS.
Stapelbalkendiagramme: Anteile vom Ganzen
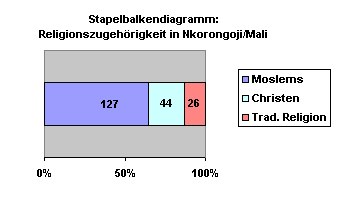
Stapelbalkendiagramme werden - neben Kreisdiagrammen - oft verwendet, um Anteile am Ganzen darzustellen. Zur Darstellung von relativen Mehrheiten sind sie etwas weniger übersichtlich als Kreisdiagramme.
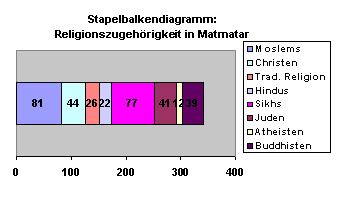
Auch sie werden sehr schnell unübersichtlich, wenn die Kategorien zu zahlreich werden, bleiben bei einer größeren Zahl von Subeinheiten aber noch übersichtlicher als Kreisdiagramme:
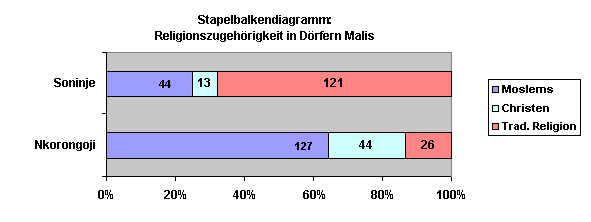
Vergleich der Aufteilung: Stapelbalkendiagramme
Gestapelte Balkendiagramme sind besonders wertvoll beim Vergleich der Aufteilung der gleichen Variable in verschiedenen Stichproben/Populationen[1].
Verweise:
[1] Siehe Kapitel 2.1
3.6.1.3.1 Gruppierte Balkendiagramme mit SPSS
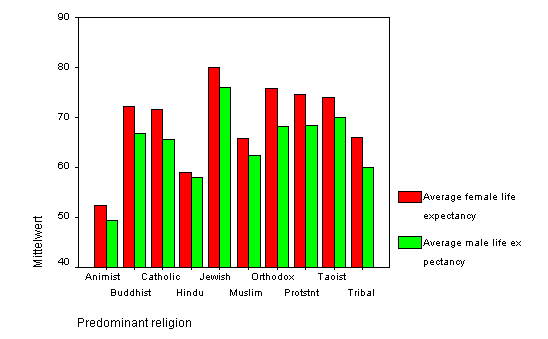
Im folgenden Diagramm interessiert uns, inwieweit sich die männliche und die weibliche Lebenserwartung in den Ländern dieser Welt nach deren religiöser Ausrichtung unterscheiden. Wir greifen dabei auf Daten in world95.sav bei der Berechnung mit SPSS zurück. Der Vorgang mit SPSS erfolgt folgendermaßen:
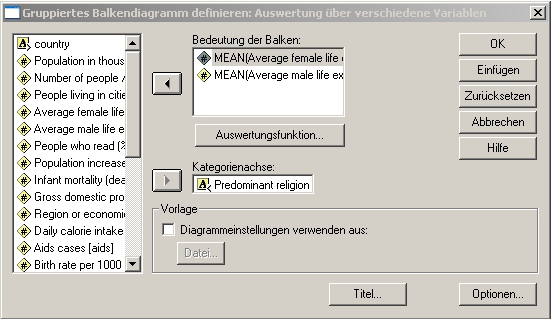
A. Klicken Sie auf GRAFIKEN - BALKEN
B. Wählen Sie das Symbol für Gruppiert und dann Auswertung über verschiedene Variablen.
C. Nun wählen wir zumindest zwei numerische Variablen aus (welche wir vergleichend zu den Religionen betrachten wollen, in unserem Falle die männliche und die weibliche Lebenserwartung). Diese schieben wir in das Feld Bedeutung der Balken:
D. Im Feld Kategorienachse fügen wir die Kategorienvariable (in unserem Falle die dominierende Religion des Landes) ein.
E. Bei Klick auf Auswertungsfunktion können wir uns für bestimmte Kennzahlen entscheiden, wie den Median[1], das arithmetische Mittel[2], die Häufigkeit[3], Summe, welche für die numerischen Variablen berechnet werden..
Nach Klick auf OK erhalten wir das folgende Diagramm:
Verweise:
[1] Siehe Kapitel 3.3.3
[2] Siehe Kapitel 3.3.2
[3] Siehe Kapitel 3.2.2
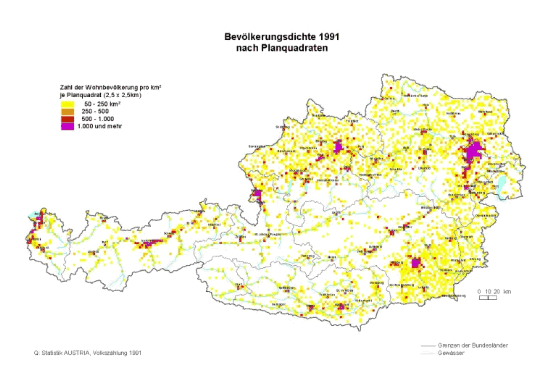
3.6.1.4 Kartogramme
Kartogramme sind eine Sonderform von Diagrammen und zeigen die Ausprägungen einer Variable auf Landkarten.
Kartogramme sind meist nur mit relativ teuren Programmen möglich, wie z.B. Arcview. Zu Excel gibt es eine billigere Zusatzsoftware wie Mapland (99-999 $). MS Office 2000 Professional enthielt noch eine vereinfachte Excel-Komponente namens Microsoft Map.
Kartogramme in Wahlanalysen häufig
Mittels Kartogrammen können v.a. regional unterschiedliche Ausprägungen sehr gut wiedergegeben werden. Sie werden z.B. bei der TV-Berichterstattung an Wahlabenden eingesetzt, um unterschiedliche Wahlpräferenzen in den verschiedenen Bundesländern und Regionen aufzuzeigen.
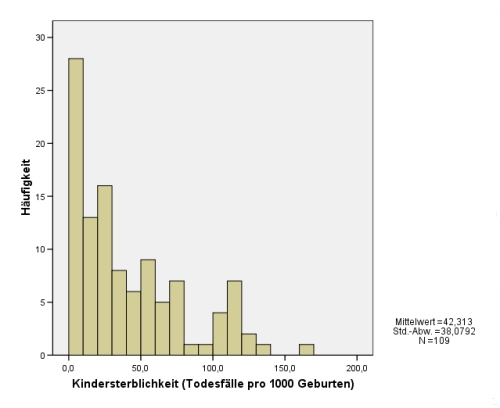
3.6.1.5 Histogramme
Unter einem Histogramm versteht man die grafische Darstellung der Häufigkeitsverteilung[1] von Messwerten.
Die Daten sind dabei größenmäßig auf der X-Achse geordnet, während auf der Y- Achse ihre Häufigkeiten stehen. Über jeder Klasse wird ein Rechteck errichtet, dessen Fläche proportional zur klassenspezifischen Häufigkeit ist.
Histogramme werden besonders zur Darstellung von Verteilungen verwendet, wie auch zur Demonstration der Normalverteilung[2].
Verweise:
[1] Siehe Kapitel 3.1.3.3.2
[2] Siehe Kapitel 3.1.3.3.1
3.6.1.6 Streudiagramme
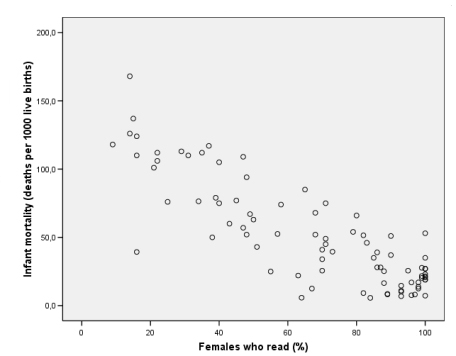
Streudiagramme (oder Punktdiagramme) ermöglichen die grafische Darstellung des Zusammenhangs von zwei Variablen.
Die Ausprägung der Variable A wird auf der X- Achse eingetragen, die Ausprägung der Variable B auf der Y-Achse.
Basierend auf UN-Daten über die Entwicklung der Länder dieser Welt (siehe world95.sav) zeigt dieses Diagramm den Zusammenhang zwischen Kindersterblichkeit und weiblicher Alphabetisierung. Man sieht deutlich, dass mit steigender Alphabetisierungsrate der Frauen die Kindersterblichkeit drastisch zurückgeht. Streudiagramme eignen sich vorzüglich zum Aufzeigen des Zusammenhangs zwischen Variablen[1] und somit auch zur Darstellung der Regression und der Korrelation[2].
Verweise:
[1] Siehe Kapitel 3.5.1
[2] Siehe Kapitel 3.5.4.2
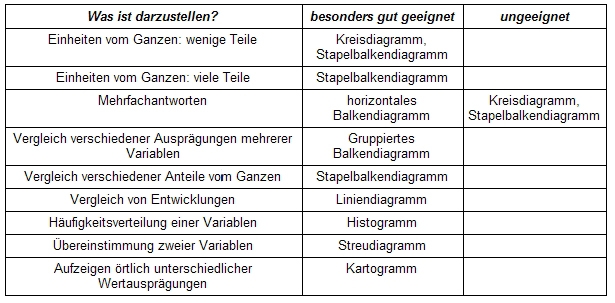
3.6.2 Welches Diagramm für welche Daten?
3.6.3 Notwendige Begleitinformationen von Diagrammen
Diagramme brauchen Begleitinformationen
Diagramme sollten genauso wie die tabellarische Darstellung statistischer Daten alle notwendigen Begleitinformationen aufweisen, die zum Verständnis des Diagramms sowie zum Nachweis der Seriösität der Arbeit wichtig sind. Dazu zählen:
A. Name des Erstellers, v.a. wenn es sich um Fremddiagramme handelt;
B. Falls es sich nicht um eigene Daten handelt, auf deren Grundlage das Diagramm erstellt wurde, sollte die Quelle der Daten angegeben werden (z.B. Statistikamt der Stadt Ulm 1997) (am besten unterhalb des Diagramms)
C. Jahr der Erhebung der Daten;
D. Größe der Stichprobe (am Besten die bereinigte Größe, welche Null-Eingaben und fehlerhafte Eingaben nicht berücksichtigt), v.a. wenn es sich um eigene Daten handelt. Bei gut bekannten Fremddatenquellen wird darauf meist verzichtet (z.B. bei Erhebungen statistischer Zentralämter etc.)
E. Angabe der Messeinheiten (cm, Zähleinheiten, Prozent etc.)
F. Aussagekräftiger Titel des Diagramms (ganz oben)
G. Aussagekräftige Bezeichnungen für die Bestandteile des Diagramms (z.B. für Daten auf der x- bzw. y-Achse.
H. Eventuell Hinweis auf Art der Erhebung der Daten
I. Bei Mehrfachantworten unbedingt Hinweis darauf
Das folgende Diagramm (Quelle: http://www.mzes.uni-mannheim.de/publications/wp/wp-89.pdf[1]) berücksichtigt diese Erfordernisse. Obwohl gleichzeitig viele Daten dargestellt werden müssen, bleibt der Erkenntnisgrad hoch.
Verweise:
[1] http://www.mzes.uni-mannheim.de/publications/wp/wp-89.pdf