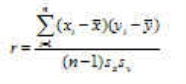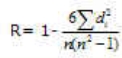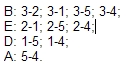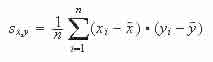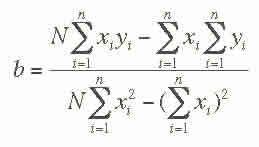Difference between revisions of "Ausgewählte statistische Grundlagen und Analysemethoden/Korrelation"
(Created page with " '''Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Streuung#3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’|Vorheriges Kapitel: 3.4 Streuungs...") |
m (Protected "Ausgewählte statistische Grundlagen und Analysemethoden/Korrelation" ([Edit=Allow only administrators] (indefinite) [Move=Allow only administrators] (indefinite)) [cascading]) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 11: | Line 11: | ||
<div class="eksa_toc"> | <div class="eksa_toc"> | ||
[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5 Der Zusammenhang zwischen Variablen|3.5 Der Zusammenhang zwischen Variablen]]<br /> | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5 Der Zusammenhang zwischen Variablen|3.5 Der Zusammenhang zwischen Variablen]]<br /> | ||
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.1 Optische Erkennung von Zusammenhängen|3.5.1 Optische Erkennung von Zusammenhängen]]<br /> | + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.1 Optische Erkennung von Zusammenhängen|3.5.1 Optische Erkennung von Zusammenhängen]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.2 Kreuztabellen-Analyse|3.5.2 Kreuztabellen-Analyse]]<br /> | + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.2 Kreuztabellen-Analyse|3.5.2 Kreuztabellen-Analyse]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.2.1 Berechnung von Kreuztabellen-Analysen mit SPSS|3.5.2.1 Berechnung von Kreuztabellen-Analysen mit SPSS]]<br /> | + | ::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.2.1 Berechnung von Kreuztabellen-Analysen mit SPSS|3.5.2.1 Berechnung von Kreuztabellen-Analysen mit SPSS]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.2.1.1 Überprüfung von Zusammenhängen mit dem Chi-Quadrat-Test|3.5.2.1.1 Überprüfung von Zusammenhängen mit dem Chi-Quadrat-Test]]<br /> | + | :::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.2.1.1 Überprüfung von Zusammenhängen mit dem Chi-Quadrat-Test|3.5.2.1.1 Überprüfung von Zusammenhängen mit dem Chi-Quadrat-Test]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.2.2 Grafische Darstellung von Kreuztabellen mit SPSS|3.5.2.2 Grafische Darstellung von Kreuztabellen mit SPSS]]<br /> | + | ::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.2.2 Grafische Darstellung von Kreuztabellen mit SPSS|3.5.2.2 Grafische Darstellung von Kreuztabellen mit SPSS]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3 Die Korrelation|3.5.3 Die Korrelation]]<br /> | + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3 Die Korrelation|3.5.3 Die Korrelation]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.1 Maßkorrelation|3.5.3.1 Maßkorrelation]]<br /> | + | ::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.1 Maßkorrelation|3.5.3.1 Maßkorrelation]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.1.1 Berechnung der Maßkorrelation mit SPSS|3.5.3.1.1 Berechnung der Maßkorrelation mit SPSS]]<br /> | + | :::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.1.1 Berechnung der Maßkorrelation mit SPSS|3.5.3.1.1 Berechnung der Maßkorrelation mit SPSS]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.2 Rangkorrelation R (Krueger-Spearman)|3.5.3.2 Rangkorrelation R (Krueger-Spearman)]]<br /> | + | ::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.2 Rangkorrelation R (Krueger-Spearman)|3.5.3.2 Rangkorrelation R (Krueger-Spearman)]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.2.1 Berechnung der Rangkorrelation mit SPSS|3.5.3.2.1 Berechnung der Rangkorrelation mit SPSS]]<br /> | + | :::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.2.1 Berechnung der Rangkorrelation mit SPSS|3.5.3.2.1 Berechnung der Rangkorrelation mit SPSS]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.3 Rangkorrelation Tau (Kendall)|3.5.3.3 Rangkorrelation Tau (Kendall)]]<br /> | + | ::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.3 Rangkorrelation Tau (Kendall)|3.5.3.3 Rangkorrelation Tau (Kendall)]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.3.1 Berechnung von TAU mit SPSS|3.5.3.3.1 Berechnung von TAU mit SPSS]]<br /> | + | :::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.3.1 Berechnung von TAU mit SPSS|3.5.3.3.1 Berechnung von TAU mit SPSS]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.4 Aussagekraft einer Korrelation|3.5.3.4 Aussagekraft einer Korrelation]]<br /> | + | ::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.4 Aussagekraft einer Korrelation|3.5.3.4 Aussagekraft einer Korrelation]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.4.1 Wann sind Korrelationen bemerkenswert?|3.5.3.4.1 Wann sind Korrelationen bemerkenswert?]]<br /> | + | :::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.4.1 Wann sind Korrelationen bemerkenswert?|3.5.3.4.1 Wann sind Korrelationen bemerkenswert?]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.4.2 Verdeckte Korrelation|3.5.3.4.2 Verdeckte Korrelation]]<br /> | + | :::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.4.2 Verdeckte Korrelation|3.5.3.4.2 Verdeckte Korrelation]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.4.3 Scheinkorrelationen und Störvariable|3.5.3.4.3 Scheinkorrelationen und Störvariable]]<br /> | + | :::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.4.3 Scheinkorrelationen und Störvariable|3.5.3.4.3 Scheinkorrelationen und Störvariable]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.4.3.1 Partielle Korrelation mit SPSS|3.5.3.4.3.1 Partielle Korrelation mit SPSS]]<br /> | + | :::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.4.3.1 Partielle Korrelation mit SPSS|3.5.3.4.3.1 Partielle Korrelation mit SPSS]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.4.4 Signifikanz der Korrelation|3.5.3.4.4 Signifikanz der Korrelation]]<br /> | + | :::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.4.4 Signifikanz der Korrelation|3.5.3.4.4 Signifikanz der Korrelation]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.4.4.1 Signifikanz mit SPSS|3.5.3.4.4.1 Signifikanz mit SPSS]]<br /> | + | :::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.4.4.1 Signifikanz mit SPSS|3.5.3.4.4.1 Signifikanz mit SPSS]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.5 Kovarianz|3.5.3.5 Kovarianz]]<br /> | + | ::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3.5 Kovarianz|3.5.3.5 Kovarianz]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.4 Regression|3.5.4 Regression]]<br /> | + | :[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.4 Regression|3.5.4 Regression]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.4.1 Statistisch-mathematische Berechnung der linearen Regression|3.5.4.1 Statistisch-mathematische Berechnung der linearen Regression]]<br /> | + | ::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.4.1 Statistisch-mathematische Berechnung der linearen Regression|3.5.4.1 Statistisch-mathematische Berechnung der linearen Regression]]<br /> |
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.4.2 Grafische Darstellung der Regression|3.5.4.2 Grafische Darstellung der Regression]]<br /> | + | ::[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.4.2 Grafische Darstellung der Regression|3.5.4.2 Grafische Darstellung der Regression]]<br /> |
</div> | </div> | ||
| Line 610: | Line 610: | ||
[[File:quantitative-113_3.jpg|frame|center|Streudiagramm mit Regressionsgerade]] | [[File:quantitative-113_3.jpg|frame|center|Streudiagramm mit Regressionsgerade]] | ||
| − | |||
'''Verweise:'''<br /> | '''Verweise:'''<br /> | ||
[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Darstellung#3.6.1.6 Streudiagramme|[1] Siehe Kapitel 3.6.1.6]]<br /> | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Darstellung#3.6.1.6 Streudiagramme|[1] Siehe Kapitel 3.6.1.6]]<br /> | ||
| − | |||
<br /> | <br /> | ||
Latest revision as of 14:32, 24 September 2020
Vorheriges Kapitel: 3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’
Contents
- 1 3.5 Der Zusammenhang zwischen Variablen
- 1.1 Inhalt
- 1.2 3.5.1 Optische Erkennung von Zusammenhängen
- 1.3 3.5.2 Kreuztabellen-Analyse
- 1.4 3.5.3 Die Korrelation
- 1.4.1 Vorsicht bei vorschneller Herstellung von Zusammenhängen
- 1.4.2 3.5.3.1 Maßkorrelation
- 1.4.3 3.5.3.1.1 Berechnung der Maßkorrelation mit SPSS
- 1.4.4 3.5.3.2 Rangkorrelation R (Krueger-Spearman)
- 1.4.5 3.5.3.2.1 Berechnung der Rangkorrelation mit SPSS
- 1.4.6 3.5.3.3 Rangkorrelation Tau (Kendall)
- 1.4.7 3.5.3.3.1 Berechnung von TAU mit SPSS
- 1.4.8 3.5.3.4 Aussagekraft einer Korrelation
- 1.4.9 3.5.3.4.1 Wann sind Korrelationen bemerkenswert?
- 1.4.10 3.5.3.4.2 Verdeckte Korrelation
- 1.4.11 3.5.3.4.3 Scheinkorrelationen und Störvariable
- 1.4.12 3.5.3.4.3.1 Partielle Korrelation mit SPSS
- 1.4.13 3.5.3.4.4 Signifikanz der Korrelation
- 1.4.14 3.5.3.4.4.1 Signifikanz mit SPSS
- 1.4.15 3.5.3.5 Kovarianz
- 1.5 3.5.4 Regression
3.5 Der Zusammenhang zwischen Variablen
verfasst von Erwin Ebermann
Zu den spannendsten Fragen gehört die Untersuchung von Zusammenhängen zwischen Variablen. Es ist naheliegend, sich die Frage zu stellen, ob es z.B. einen Zusammenhang zwischen Rassismus und Bildung bzw. Sozialisation, Einkommen, Erfahrungen gibt. Es ist denkbar, dass die Religion einer Person Auswirkungen auf ihre Kinderzahl hat; es ist denkbar, dass Menschen eher zu biologischen und meist auch teureren Lebensmittel greifen, wenn auch ihr Einkommen höher ist usw.
Um derartige Zusammenhänge aufzudecken, verfügen wir über verschiedene Methoden, wie z.B. die Kreuztabellen-Analyse oder die Korrelation(en).
Inhalt
3.5.1 Optische Erkennung von Zusammenhängen
Optische Darstellung von Zusammenhängen: das Streudiagramm
Trägt man auf einer Matrix von links nach rechts die Ausprägungen für die Variable A ein und die Ausprägungen für die Variable B auf der Y- Achse, so erhält man eine Reihe von Schnittpunkten. Das sich aus den Schnittpunkten ergebende Diagramm wird auch Verteilungsgrafik (auch Streuungsdiagramm, Streudiagramm oder Scatterplot genannt).
Herstellung eines Streudiagramms
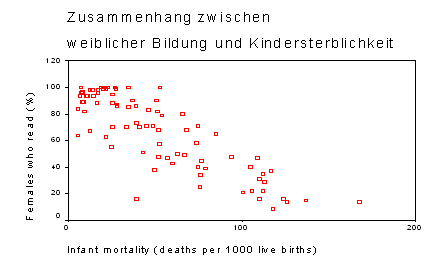
Streudiagramme eignen sich zur grafischen Darstellung bivariater Daten, also zur Darstellung von Wertepaaren in einem Koordinatensystem. An Lage und Dichte des Punkteschwarms lässt sich anschaulich ablesen, ob ein Zusammenhang zwischen den Variablen besteht. Sie werden folgendermaßen erstellt: Man trägt in einem Diagramm jeweils die Schnittpunkte der beiden Variablen ein, wobei der Wert der 1. Variablen auf der X- Achse, der Wert der 2. Variable auf der Y- Achse liegt. Im Beispiel unten trägt man auf der X- Achse den Alphabetisierungsgrad des Landes ein, auf der Y-Achse das Bruttonationalprodukt des gleichen Landes. Wo beide Einträge aufeinander treffen, wird eine Markierung (ein Punkt) eingefügt.
Zusammenhänge bereits visuell erkennbar
Hier erkennen wir bereits optisch einen gewissen Zusammenhang. Die meisten Schnittpunkte befinden sich links oben und gehen in einer Linie nach rechts unten. Man könnte durch die Schnittpunkte annäherungsweise eine Gerade[1] ziehen, die von rechts oben nach links unten geht. Man spricht hier von einem linearen Zusammenhang.
Die Aussage der Grafik ist: je höher der Alphabetisierungsgrad der Frauen, desto niedriger die Kindersterblichkeit.
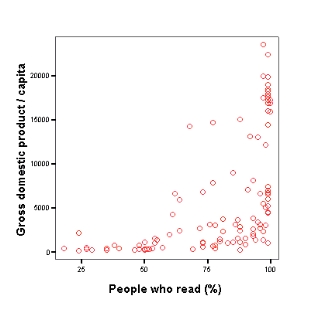
Aus diesem Diagramm ist ersichtlich, dass ein gewisser Zusammenhang zwischen Alphabetisierungsrate und BNP besteht. Länder mit nur geringer Alphabetisierungsrate haben ausnahmslos ein sehr niedriges BNP, mit hoher Alphabetisierungsrate steigt die Wahrscheinlichkeit, auch ein sehr hohes BNP aufzuweisen, doch liegen die Werte bei hoher Alphabetisierungsrate extrem auseinander. Hier lässt sich wesentlich schwerer eine Gerade ziehen, es liegt nur mehr bedingt ein linearer Zusammenhang vor.
Nachfolgend verschiedene weitere Diagramme, welche teilweise deutliche Zusammenhänge zeigen (wie oben links) oder keinerlei Zusammenhang (wie unten links). Diskutieren Sie in der Gruppe die Art der Zusammenhänge in den restlichen Diagrammen.
Verweise:
[1] Siehe Kapitel 3.5.4.2
3.5.2 Kreuztabellen-Analyse
Unter Kreuztabellen (auch Kontingenztafeln genannt) versteht man die tabellarische Darstellung der Häufigkeiten[1], welche bei der Kombination der Ausprägungen von zwei oder mehr Variablen auftreten.
Wenn z.B. zwei Variablen vorliegen, werden die Ausprägungen der Variablen A in Spalten von links nach rechts und die Ausprägungen der Variablen B in Zeilen von oben nach unten eingetragen. In jeder einzelnen Zelle wird sodann die spezifische Häufigkeit der jeweiligen Kombination Ausprägung der Variablen A mit Ausprägung der Variablen B vermerkt.
Verweise:
[1] Siehe Kapitel 3.1.3.3.2
3.5.2.1 Berechnung von Kreuztabellen-Analysen mit SPSS
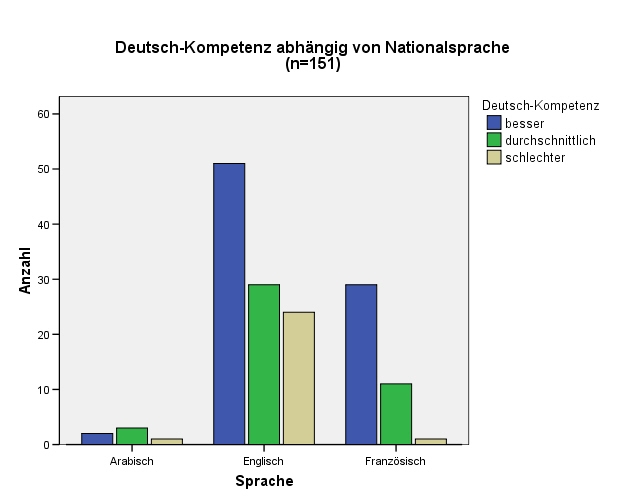
Wir möchten mit einer Kreuztabelle zeigen, wie gut in Wien lebende AfrikanerInnen nach (überprüften) Eigenangaben Deutsch beherrschen und überprüfen, ob ihre Sprachkompetenz im Deutschen mit ihrer Nationalsprache zusammenhängt.
Dazu klicken wir in SPSS auf ANALYSIEREN - DESKRIPTIVE STATISTIKEN - KREUZTABELLEN. In den Zeilen klicken wir die Herkunftssprache an, unter Spalten die Sprachkompetenz im Deutschen. Nach Klicken auf OK erhalten wir bereits folgende Tabelle:
Man kann die Ergebnisse leichter interpretieren, wenn auch die relativen Häufigkeiten[1] ermittelt werden. Dazu klicken wir unter Zellen auf zeilenweise Prozentwerte:
Nun können wir sofort erkennen, dass in unserer Stichprobe die durchschnittlichen Deutschkenntnisse der Zuwanderer aus Ländern mit französischer Nationalsprache besser als die aus Ländern mit englischer Nationalsprache sind. 70,7 % der Frankophonen sprechen besser Deutsch, aber nur 49,0 % der Anglophonen.
Verweise:
[1] Siehe Kapitel 3.1.3.3.2
3.5.2.1.1 Überprüfung von Zusammenhängen mit dem Chi-Quadrat-Test
Der Chi-Quadrat-Test, angewandt auf Kreuztabellen, ermittelt die Wahrscheinlichkeit[1], ob Zusammenhänge mehr als nur zufälliger Natur sind.
Im vorigen Beispiel (Kreuztabelle) sahen wir, dass offensichtlich ein deutlich höherer Prozentsatz von frankophonen AfrikanerInnen besser Deutsch spricht als Anglophone. Wir wissen jedoch noch nicht, ob diese Unterschiede auch signifikant sind.
Berechnung des Chi-Quadrat-Tests mit SPSS
Dazu wählen wir unter ANALYSIEREN - DESKRIPTIVE STATISTIKEN - KREUZTABELLEN den Punkt Statistik, setzen dort bei Chi-Quadrat ein Häkchen und erhalten als zusätzliche Ausgabe:
Für uns interessant ist hier der Wert für Asymptotische Signifikanz. Dort wird 0,023 aufgeführt, also ein Wert kleiner als 0,05. Damit ist mit einer Wahrscheinlichkeit von mehr als 95 % anzunehmen (oder mit einer Irrtumswahrscheinlichkeit von weniger als 5 %), dass tatsächlich ein Zusammenhang zwischen Nationalsprache und Sprachkompetenz im Deutschen besteht. Bei einem Wert > 0,01 wäre die Wahrscheinlichkeit eines Zusammenhangs sogar größer als 99 %, also wäre das Ergebnis hoch signifikant[2].
Verweise:
[1] Siehe Kapitel 1.3
[2] Siehe Kapitel 1.3.2
3.5.2.2 Grafische Darstellung von Kreuztabellen mit SPSS
Die Ergebnisse von Kreuztabellen können mit Gruppierten Balkendiagrammen[1] besonders anschaulich dargestellt werden.
Mit SPSS ist deren Erstellung sehr einfach.
Klicken Sie auf ANALYSIEREN - DESKRIPTIVE STATISTIKEN - KREUZTABELLEN und machen Sie ein Häkchen beim Punkt Gruppierte Balkendiagramme anzeigen.
Spielen Sie mit den einzelnen Elementen dieser Grafik herum. Beim Doppelklick auf Details dieses Diagramms werden sich viele Einstellmöglichkeiten öffnen.
Verweise:
[1] Siehe Kapitel 3.6.1.3
3.5.3 Die Korrelation
Unter einer Korrelation versteht man eine Kennzahl für den Zusammenhang zwischen Variablen. Prinzipiell können folgende Zusammenhänge bestehen:
- Übereinstimmung: je höher der Wert der Variablen A, desto höher ist meist auch der Wert der Variablen B: positive Korrelation
- Gegensatz: je höher Variable A, desto niedriger ist meist die Variable B: negative Korrelation
- Unabhängigkeit: Hohe Werte von A können relativ beliebigen Werten von B entsprechen und umgekehrt: keine Korrelation
Korrelationskoeffizienten können Werte zwischen -1,00 und +1,00 annehmen. Ein Wert von -1,0 bedeutet eine perfekte negative Korrelation: Hohe Werte der Variablen A gehen ausnahmslos mit niedrigen Werten der Variablen B einher und umgekehrt. Ein Wert von (+)1,0 bezeichnet eine perfekte positive Korrelation: hohe Werte von A entsprechen praktisch immer hohen Werten von B und umgekehrt.
Je nach Art der Grundskalierung[1] muss man zu unterschiedlichen Korrelationskoeffizienten greifen:
Vorsicht bei vorschneller Herstellung von Zusammenhängen
Gefundene Korrelationen müssen dennoch nochmals kritisch hinterfragt werden. Es gibt z.B. Scheinkorrelationen[2], die nur deshalb auftreten, weil beide Variablen hoch mit einer dritten Variable korrelieren, und verdeckte Korrelationen[3], bei welchen sich Subgruppen der Stichprobe[4] gegenseitig neutralisieren, selbst aber eine hohe Korrelation bei den beiden Variablen aufweisen. Erst die Signifikanz[5] gibt einer Korrelation die nötige Aussagekraft.
Verweise:
[1] Siehe Kapitel 3.1.2
[2] Siehe Kapitel 3.5.3.4.3
[3] Siehe Kapitel 3.5.3.4.2
[4] Siehe Kapitel 2.1.1
[5] Siehe Kapitel 3.5.3.4.4
3.5.3.1 Maßkorrelation
Der am häufigsten verwendete Korrelationskoeffizient ist der die Maßkorrelation beschreibende Pearsonsche Korrelationskoeffizient (Pearsons r). Er wird auch linearer Korrelationskoeffizient genannt.
Voraussetzungen zu seiner Anwendung:
• der Zusammenhang zwischen X und Y ist (annähernd) linear[1],
• beide Variablen sind normalverteilt[2].
Die Berechnung der Maßkorrelation r erfolgt durch folgende Formel:
Verweise:
[1] Siehe Kapitel 3.5.4.2
[2] Siehe Kapitel 3.1.3.1
3.5.3.1.1 Berechnung der Maßkorrelation mit SPSS
Beispiel:
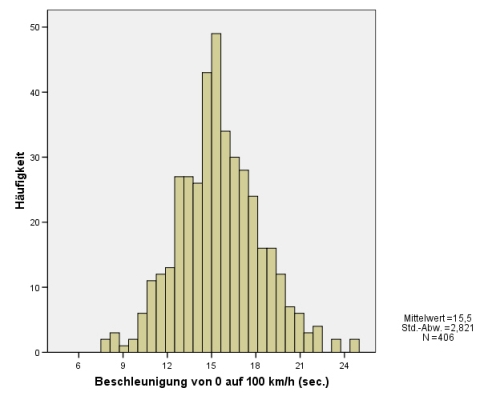
Wir möchten bei Fahrzeugen den Zusammenhang zwischen Gewicht und Beschleunigung feststellen. Wir kontrollieren mithilfe eines Histogramms[1], ob die beiden Variablen annähernd normalverteilt[2] sind:
Kontrolle der ersten Bedingung (Normalverteilung)
Kontrolle der 2. Bedingung (linearer Zusammenhang)
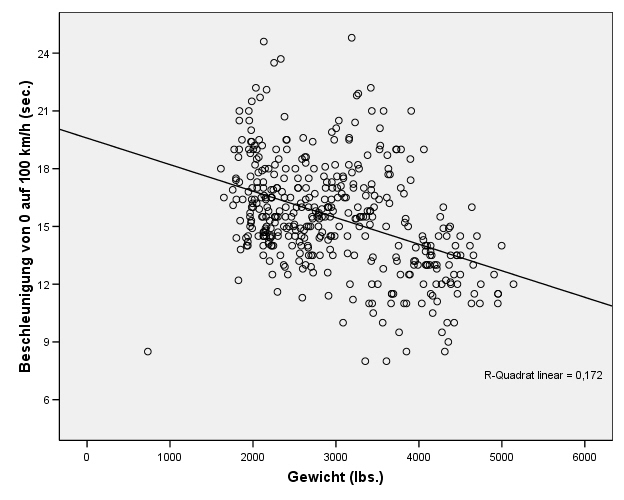
Dann erstellen wir ein Streudiagramm, welches uns einen Einblick gibt, ob die beiden Variablen systematische Entsprechungen zeigen und versuchen, in diese eine Regressionsgerade zu legen[3]. Falls dies möglich ist, ist auch die zweite Bedingung zur Anwendung der Maßkorrelation erfüllt.
Wir sehen einen merkbaren, wenn auch nicht extrem eindeutigen linearen Zusammenhang. Nun haben wir die Voraussetzungen geprüft, um diese Korrelationsberechnung anwenden zu können.
Berechnung der Maßkorrelation mit SPSS:
Klicken Sie in der Menüleiste auf ANAYLISEREN - KORRELATION - BIVARIAT und wählen Sie dort die entsprechende Korrelationsform, nämlich die nach Pearson. Im Feld Variablen fügen Sie die beiden Variablen ein, deren Zusammenhang Sie berechnen möchten. Klicken Sie auf OK:
Ergebnis des Beispiels:
Es gibt einen nachweisbaren Zusammenhang zwischen der Beschleunigung von Fahrzeugen und ihrem Gewicht. Dieser Zusammenhang ist mit einer Irrtumswahrscheinlichkeit von 1 % signifikant[4]. Da es eine negative Korrelation ist, kann man sagen, dass mit steigendem Gewicht des Fahrzeugs seine Beschleunigung abnimmt, was nicht weiter überraschend ist.
Verweise:
[1] Siehe Kapitel 3.6.1.5
[2] Siehe Kapitel 3.1.3.1
[3] Siehe Kapitel 3.5.4.2
[4] Siehe Kapitel 3.5.3.4.4
3.5.3.2 Rangkorrelation R (Krueger-Spearman)
Die Rangkorrelation R (nach Krueger- Spearman) wird v.a. bei der Auswertung psychologischer, pädagogischer und soziologischer Untersuchungen verwendet, wenn also keine wissenschaftlichen Maßeinheiten vorhanden sind, dennoch aber z.B. eine Reihung nach Größe und Intensität sinnvoll sein kann.
Z.B. kann man Kameradschaftlichkeit oder Egoismus kaum sinnvoll in Zahlenwerten messen, aber dennoch Menschen ersuchen, Mitmenschen bezüglich dieser Eigenschaften rangzureihen.
Auch verwendet für Zusammenhänge zwischen metrischen und ordinalskalierten Daten
Man setzt die Rangkorrelation häufig auch ein, wenn man den Zusammenhang von ordinalskalierten[1] und metrischen[2] Variablen berechnen möchte. Dabei wandelt man die Messwerte zuerst in Rangplätze um (nachdem man diese größenmäßig gereiht hat) um danach R berechnen zu können. Fallen mehrere umgewandelte Messwerte auf den gleichen Rangplatz, teilen sie sich diese Plätze (arithmetisches Mittel), also 6., 7., 8. und 9. Platz = 30 (6+7+8+9). 30 dividiert durch 4 (Anzahl der Rangplätze) =7,5. Jeder dieser 4 gleichen Messwerte erhält somit den Rangplatz 7,5.
Berechnung der Rangkorrelation:
R= 1-, di= Differenz des Rangplatzpaares (xi-yi); n= Anzahl der Rangplätze
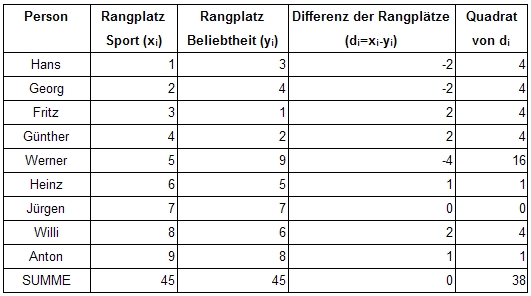
Beispiel:
Berechnung R= 1-(6*38)/(9*(81-1) = 0,68
Verweise:
[1] Siehe Kapitel 3.1.2.3
[2] Siehe Kapitel 3.1.1.1
3.5.3.2.1 Berechnung der Rangkorrelation mit SPSS
Klicken Sie in der Menüleiste auf ANALYSIEREN - KORRELATION - BIVARIAT und wählen Sie dort die entsprechende Korrelationsform, nämlich die nach Spearman. Im Feld Variablen fügen Sie die beiden Variablen ein, deren Zusammenhang Sie berechnen möchten. Falls die Variablen über höherwertige Skalierungen[1] als die Ordinalskala[2] verfügen (Intervall-[3] oder Proportionalskala[4]), werden sie automatisch von SPSS in die entspechenden Rangplätze umgewandelt. Klicken Sie dann auf OK. Sie erhalten die Ausgabe der Korrelation gemeinsam mit der Beurteilung ihrer Signifikanz[5].
Verweise:
[1] Siehe Kapitel 3.1.2
[2] Siehe Kapitel 3.1.2.3
[3] Siehe Kapitel 3.1.2.4
[4] Siehe Kapitel 3.1.2.5
[5] Siehe Kapitel 3.5.3.4.4
3.5.3.3 Rangkorrelation Tau (Kendall)
Die Rangkorrelation TAU (nach Kendall) wird häufig verwendet, wenn N, also die Gesamtanzahl an Fällen, sehr niedrig ist (< 20).
Berechnung: Zuerst werden alle Ausprägungen der beiden Variablen in Ränge umgewandelt.
Danach wird eine Variable größenmäßig sortiert (nach Rangplätzen), die zum gleichen Fall gehörenden Rangplätze der anderen Variablen werden darunter geschrieben:
Die 1. Rangreihe ist bereits größenmäßig sortiert. In der 2. Rangreihe wird nun verglichen, ob die Rangordnung der 1. Rangreihe (Schulbildung) eingehalten wird. D.h. bei einer maximalen positiven Korrelation von Schulbildung und Schichtzugehörigkeit müsste bei Schichtzubehörigkeit ebenfalls B den 1. Platz haben, E den 2., D den 3. usw., bei einer negativen Korrelation selbstverständlich umgekehrt.
Für jede Person der 2. Rangreihe (Schichtzugehörigkeit) wird nun verglichen, ob auf sie folgenden Rangzahlen größer oder kleiner sind. ’Richtig’ wäre eine größere nach einer kleineren Rangzahl; ’falsch’ eine kleinere nach einer größeren Rangzahl:
Insgesamt überprüfen wir 10 Zahlenpaare. Für jede 'richtige' Zahlenfolge zählen wir ein "Plus", für jede 'falsche' Reihenfolge ein "Minus".
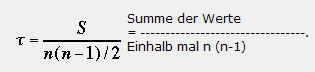
Wir zählen 6-Plus und 4-Minuszeichen, zieht man die Minus von den Plus ab, ergibt sich die Summe S = 2. Diese Summe S wird bei der Berechnung von Tau mit der höchstmöglichen Summe dieser Art Smax verglichen.
Smax errechnet sich aus N(N-1)/2, denn die Gesamtzahl von Paarvergleichen hängt nur von N (also der Länge der Rangreihe ab). Ist die zweite Rangreihe identisch mit der ersten (geordneten), so ergeben sich beim Paarvergleich nur ’richtige’ Reihenfolgen und die Gesamtsumme des "Plus- Zeichen" ist gleich der Summe der insgesamt möglichen Paarvergleiche Smax.
Tau ergibt sich als TAU = S/Smax.
In unserem Beispiel ist Smax = 5*4/2 = 10. TAU ist also gleich 2/10 = 0,2
Diese Berechnungsart sollte nur dann angewendet werden, wenn innerhalb einer Rangreihe keine geteilten Rangplätze auftreten.
3.5.3.3.1 Berechnung von TAU mit SPSS
Klicken Sie in der Menüleiste auf ANAYLISEREN - KORRELATION - BIVARIAT und wählen Sie dort die entsprechende Korrelationsform, nämlich Kendall-Tau. Im Feld Variablen fügen Sie die beiden Variablen ein, deren Zusammenhang Sie berechnen möchten. Falls die Variablen über höherwertige Skalierungen[1] als die Ordinalskala[2] verfügen (Intervall[3] - oder Proportionalskala[4]), werden sie automatisch umgewandelt. Klicken Sie dann auf OK. Sie erhalten die Ausgabe der Korrelation gemeinsam mit der Beurteilung ihrer Signifikanz[5].
Verweise:
[1] Siehe Kapitel 3.1.2
[2] Siehe Kapitel 3.1.2.3
[3] Siehe Kapitel 3.1.2.4
[4] Siehe Kapitel 3.1.2.5
[5] Siehe Kapitel 3.5.3.4.4
3.5.3.4 Aussagekraft einer Korrelation
Die Aussagekraft einer Korrelation hängt von mehreren Faktoren ab:
A. der Höhe der Korrelation
B. der Größe der Stichprobe[1](n)
C. der Sorgfalt beim Ausschluss einer möglichen Scheinkorrelation bzw. des Erkennens verdeckter Korrelationen.
Die statistische Kennzahl der Signifikanz berücksichtigt sowohl die Höhe der Korrelation wie auch die Größe der Stichprobe und gibt Auskunft über die Wahrscheinlichkeit[2], dass die erhaltene Korrelation rein zufällig auftrat. Sie ist statistisch von äußerst großer Bedeutung.
Verweise:
[1] Siehe Kapitel 2.1.1
[2] Siehe Kapitel 1.3.2
3.5.3.4.1 Wann sind Korrelationen bemerkenswert?
Die Größe einer Korrelation sagt alleine noch nichts über ihre Aussagekraft aus. Prinzipiell gilt, dass eine hohe Korrelation umso leichter zu erzielen ist, je kleiner die Stichprobe ausfällt. Bei einer Stichprobengröße von 1 liegt jede Korrelation beim Maximalwert r=1.
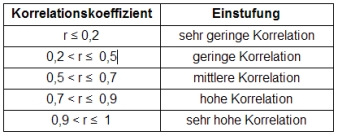
Bei kleineren Stichproben (etwa n=20) sind folgende Einschätzungen von r bzw. R weitverbreitet:
Ob eine Korrelation bedeutend oder unbedeutend ist, hängt auch von der Art des (überraschenden) Zusammenhangs ab. Eine hohe Korrelation der Schuhgröße mit der Körpergröße von r=0,8 ist deutlich weniger bedeutend als eine gesicherte Korrelation von r=0,4 bei einer großen Stichprobe über den Zusammenhang zwischen dem Konsum eines bestimmten Nahrungsmittels und der Entwicklung einer bestimmten Krankheit.
3.5.3.4.2 Verdeckte Korrelation
Von einer verdeckten Korrelation spricht man, wenn statistisch keinerlei Korrelation errechnet wurde, obwohl sachlich eindeutig Zusammenhänge vorliegen.
Dies ist z.B. möglich, wenn Subgruppen der untersuchten Population in hohem Maße Tendenzen aufweisen, welche durch andere Subgruppen neutralisiert werden, weil diese sich gegenläufig verhalten.
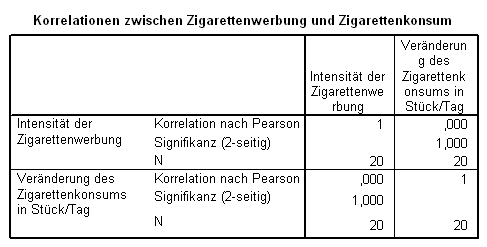
Fiktives Beispiel: Zusammenhang von Zigarettenkonsum und -werbung
Wir untersuchen, welchen Einfluss ein unterschiedlich intensiver Kontakt mit einer bestimmten Tabak-Werbung auf das Rauchverhalten von Jugendlichen ausübt. Wir stellen fest, dass es keinen messbaren Zusammenhang zwischen dem Konsum der Werbung und dem Zigarettenkonsum gibt. Der Zigarettenkonsum hat sich durch die Wahrnehmung der Werbung nicht verändert.
Ein Blick auf die zugrundeliegenden Daten zeigt jedoch, dass es sehr wohl einen substantiellen Zusammenhang geben muss. Wir betrachten dazu ein Histogramm (In SPSS -> GRAFIKEN - HISTOGRAMM), bei welchem wir die Werbung als Variable eintragen, die Veränderung des Zigarettenkonsums in Felder anordnen als und unter Variable verspachteln das Geschlecht eintragen.
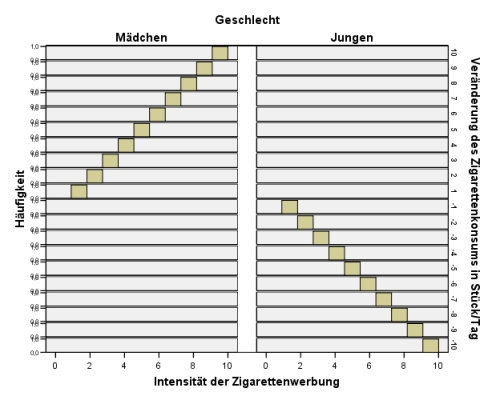
Wir erhalten dann folgende zwei nach Geschlechtern getrennte Histogramme:
Wir sehen, dass bei den Jungen eine perfekte negative Korrelation[1] vorliegt (r=-1), bei den Mädchen hingegen eine perfekte positive Korrelation (r=1). Die Jungen haben die Werbung eher als erschreckend für den Tabakkonsum aufgefasst, die Mädchen hingegen als ermutigend. Am Ende des Untersuchungszeitraums rauchten die Mädchen im gleichen Maße mehr als die Jungen weniger rauchten. Dadurch ergab sich eine Null-Korrelation auf der Ebene der gesamten Stichprobe[2].
Verweise:
[1] Siehe Kapitel 3.5.3
[2] Siehe Kapitel 2.1.1
3.5.3.4.3 Scheinkorrelationen und Störvariable
Eine Scheinkorrelation ist ein statistisch gemessener Zusammenhang zwischen zwei Variablen, welcher nur deshalb auftritt, weil beide Variablen systematisch von einer dritten Variablen beeinflusst werden.
Zusammenhang kann auf Störfaktoren zurückgehen
Die Korrelation ist eine interessante Methode zur Berechnung von Zusammenhängen. Jedoch sollte man sich vergewissern, dass der gemessene Zusammenhang tatsächlich prioritär und somit kausal ist.
Es ist immer auch möglich, dass andere Erklärungen (Störfaktoren) für den Zusammenhang übersehen wurden, was zu Scheinkorrelationen führen kann.
Beispiel 1: Bringen Störche Kinder?
So zeigt sich in Untersuchungen verschiedener Länder ein hoher Zusammenhang zwischen der Storchenpopulation und der Geburtenrate (teilweise bis r=0,7) im Laufe der Jahrzehnte. Die Erklärung dieses verblüffenden Zusammenhanges ist einfach: Durch bessere Bildungs- und Berufschancen der Frauen ging die Geburtenrate zurück, durch zunehmende Umweltbelastung die Storchenpopulation. Daher ist der Zusammenhang von Storchenpopulation und Geburtenrate rein zufällig. Er ergibt sich statistisch einfach dadurch, dass sowohl Storchenpopulation wie auch Geburtenrate hoch mit der Wirtschaftsentwicklung korrelieren. Diese führte zu besseren Jobchancen für Frauen und dadurch auch zu geringeren Kinderzahlen wie auch zu einer zunehmenden Umweltbelastung und damit zu sinkenden Storchenpopulationen.
Beispiel 2: Haben reichere Männer weniger Haare?
Es lässt sich ein hoher Zusammenhang zwischen Männern mit schütterem Haar und hohem Einkommen nachweisen. Tatsächlich besteht aber eher ein Zusammenhang zwischen dem Alter der Männer und ihrem Einkommen und mit zunehmendem Alter nimmt auch die Zahl der Haare ab.
Ist man unsicher, ob eine errechnete Korrelation haltbar ist, kann man kann mögliche Störfaktoren mit der Partiellen Korrelation herausfiltern.
3.5.3.4.3.1 Partielle Korrelation mit SPSS
Beispiel: Korrelation von Fertiliät und weiblicher Lebenserwartung
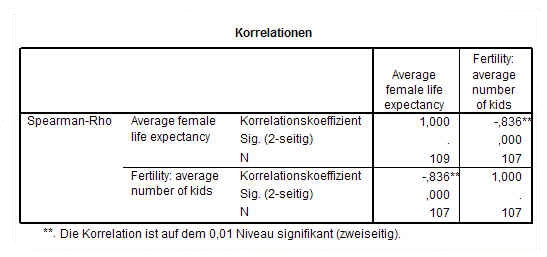
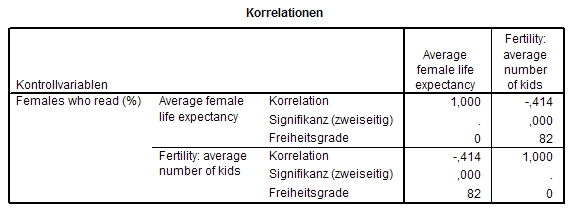
Wir untersuchen den Zusammenhang zwischen Fertilität und weiblicher Lebenserwartung (basierend auf den Daten in world95.sav der UNO). Eine Rangkorrelation zwischen beiden liefert folgendes Resultat:
Überlegung:
Wir sehen einen hohen und signifikanten Zusammenhang zwischen beiden Variablen. Offensichtlich führt eine große Kinderzahl zu stark abnehmender weiblicher Lebenserwartung und umgekehrt. Doch warum sollte dies so sein? Wir kennen doch Personen in unserer Gesellschaft, welche viele Kinder haben und dennoch in voller Gesundheit sehr alt wurden, während wir auch viele kränkliche einzelstehende Personen kennen. Wir suchen daher nach Variablen, welche die beiden vorhandenen beeinflusst haben könnten und dadurch indirekt deren hohen Zusammenhang begründen. Eine derartige mögliche (Stör-)variable ist die weibliche Alphabetisierungsrate. Sie verbessert den Zugang zu Informationen über verbesserte Gesundheitsvorsorge. Damit erhöht sie die Lebenserwartung. Gleichzeitig bietet sie durch verbesserte Berufschancen in qualifizierteren Bereichen auch häufig bessere Einkommensschancen. Bleibt eine gut verdienende Frau wegen zahlreicher Kinder zuhause, stellt dies gleichzeitig für die Familie einen größeren finanziellen Verlust dar, wie wenn eine schlecht verdienende Frau zuhause bleiben würde. Daher entscheiden sich gebildete Frauen häufig gegen höhere Kinderzahlen. Auch wird die Geburt der ersten Kinder oft hinter den abgeschlossenen Bildungsweg zurückgeschoben, was ebenfalls die Fertilität verringert.
Das waren sachliche Argumente. Die Korrelationen stützen diese Annahme:
Herausrechnung der Störvariable mit SPSS:
Um nun den Einfluss der Störvariable aus der Beziehung weibliche Lebenserwartung/Geburtenrate herauszurechnen, gehen wir in SPSS folgendermaßen vor:
Klicken Sie in der Menüleiste auf ANAYLISEREN - KORRELATION - PARTIELLE KORRELATIONEN.
Im Feld Variablen fügen Sie die beiden Variablen ein, deren Zusammenhang Sie berechnen möchten. Unter Kontrollvariablen fügen Sie die Störvariable ein. Klicken Sie dann auf OK. Sie erhalten die Ausgabe der Korrelation gemeinsam mit der Beurteilung ihrer Signifikanz.
Sie sehen, dass durch den Ausschluss dieser Störvariable die Korrelation zwischen der weiblichen Lebenserwartung und der Fertilität auf die Hälfte gesunken ist.
3.5.3.4.4 Signifikanz der Korrelation
Die Signifikanz ist eine Kennzahl, welche die Wahrscheinlichkeit eines systematischen Zusammenhangs zwischen den Variablen bezeichnet. Sie drückt aus, ob ein scheinbarer Zusammenhang rein zufälliger Natur sein könnte oder mit hoher Wahrscheinlichkeit[1] tatsächlich vorliegt. Man spricht bei der Signikanz von Irrtumswahrscheinlichkeiten oder Signifikanzniveaus. Gängige Formulierungen lauten etwa, dass zwischen den Variablen A und B eine Korrelation von r=0,5 auf dem Signifikanzniveau oder der Irrtumswahrscheinlichkeit von p ≤ 1 % besteht. Dies bedeutet, dass die zwischen den Variablen A und B gefundene Korrelation in dieser Höhe und bei dieser Stichprobengröße nur in weniger als 1 % aller Fälle rein zufällig auftritt.
Die Kennzahl p der Irrtumswahrscheinlichkeit, auf deren komplexe Berechnung hier nicht eingegangen wird, berücksichtigt somit sowohl die Höhe der Korrelation wie auch die Größe der Stichprobe. Ist die Stichprobe[2] sehr klein, muss die Korrelation extrem groß ausfallen, um signifikant sein zu können. Hingegen kann auch eine Korrelation von r=0,2 bei sehr großen Stichproben signifikant werden.
Grenzwerte der Signifikanz bei n=20
Für eine Stichprobe der Größe n = 20 finden wir für einseitige Irrtumswahrscheinlichkeit (Signifikanz) folgende Grenzwerte:
Irrtumswahrscheinlichkeit p ≤ 5 %: r/R/TAU muss größer sein als 0,377
Irrtumswahrscheinlichkeit p ≤ 1 %: r/R/TAU muss größer sein als 0,534
D.h. wenn man eine Korrelation von 0,6 bei einer Stichprobe von n=20 ermittelt, dann ist die Wahrscheinlichkeit geringer als 1 %, dass dieser Zusammenhang rein zufälliger Natur ist.
Bestimmtheitsmaß: Anteil der Korrelation an Veränderung
Wenn der Korrelationskoeffizient quadriert wird, erhält man das Bestimmtheitsmaß (R2), den Anteil der durch eine Variable erklärten Streuung an der Streuung der anderen. R/r=0,8 bedeutet nicht, dass 80 % der Stichprobe einander entsprechen. R2 gibt Aufschluss darüber, dass 0,8*0,8=0,64 = 64 % der Variabilität der Werte beider Variablen durch den Zusammenhang bestimmt sind.
Verweise:
[1] Siehe Kapitel 1.3.2
[2] Siehe Kapitel 2.1.1
3.5.3.4.4.1 Signifikanz mit SPSS
Signifkanz von Korrelationen wird von SPSS automatisch ermittelt
Statistikprogramme wie SPSS ermitteln selbstständig bei der Berechnung der Korrelation die dazugehörige Irrtumswahrscheinlichkeit. Bei SPSS wird mit Sternen ausgedrückt (1, 2 oder 3 Sterne), ob die Korrelation signifikant ist, d.h. ob der Zusammenhang weitgehend gesichert scheint oder nicht.
Drei wesentliche Schwellen der Irrtumswahrscheinlichkeit[1] haben breite Akzeptanz gefunden:
- p <= 0,05 (die Wahrscheinlichkeit einer rein zufälligen Korrelation liegt bei unter 5 %, SPSS vergibt einen Stern = *);
- p <= 0,01 (die Irrtumswahrscheinlichkeit ist kleiner als 1 %, SPSS vergibt 2 Sterne **) oder
- p <= 0,001 (die Irrtumswahrscheinlichkeit ist kleiner als 1 ‰, SPSS vergibt 3 Sterne ***).
Diese Korrelation zeigt, basierend auf UNO- Statistiken aus dem Jahr 1995, den Zusammenhang zwischen der täglichen Kalorienaufnahme und dem Bruttonationalprodukt von Ländern. Defaultmäßig berechnet SPSS zur Korrelation auch die Signifikanz der Korrelation und markiert signifikante Korrelationen wie in diesem Beispiel mit Sternchen. Diese Korrelation ist signifikant auf dem 1%-Niveau (2 Sternchen). Damit signifikante Korrelationen automatisch mit Sternchen markiert werden, muss im Fenster der Korrelationsberechnung der Punkt signifikante Korrelationen markieren mit einem Häkchen markiert sein.
Verweise:
[1] Siehe Kapitel 1.3.2
3.5.3.5 Kovarianz
Die Kovarianz ist eine Kennzahl für den Zusammenhang von zwei Variablen. Sie entspricht der Summe der gemittelten Abweichungsprodukte der Variablen. Sie wird nach folgender Formel berechnet:
Die Kovarianz ist positiv, wenn X und Y tendenziell einen linearen Zusammenhang besitzen, d. h. hohe Werte von X entsprechen hohen Werten von Y und niedrige Werte von X niedrigen Werten von Y.
Die Kovarianz ist negativ, wenn X und Y einen gegensinnigen linearen Zusammenhang aufweisen, d. h. hohe Werte von X gehen einher mit niedrigen Werten von Y und umgekehrt.
Da die Kovarianz in ihrer Rohform von der Größe der zugrundeliegenden Daten abhängt, ist die Einschätzung ihres Wertes ohne die Kenntnis der zugrundeliegenden Daten nicht einschätzbar. Dazu muss sie erst standardisiert werden, was zur Korrelation[1] führt.
Verweise:
[1] Siehe Kapitel 3.5.3
3.5.4 Regression
Die Regression(sanalyse) ist ein Verfahren zur Analyse von Beziehungen zwischen einer abhängigen und einer oder mehreren unabhängigen Variablen. Während die Korrelation[1] die Stärke eines Zusammenhangs zeigt, erlaubt es die Regression, von einer bekannten Größe einer Variable auf die vermutliche Größe der abhängigen Variablen zu schließen, falls ein systematischer Zusammenhang zwischen zwei Variablen A und B vorliegt.
Prinzipiell unterscheidet man zwischen linearer und nicht-linearer Regression.
Bei der linearen Regression kann eine Art Regressionsgerade ins Histogramm gelegt werden, welche die Möglichkeit der annähernden Voraussage von Ausprägungen bietet.
Der Verlauf der Regressionsgerade wird über die Formel
y = b*x + a
ermittelt, wobei b den Regressionskoeffizienten darstellt, welcher den Tangens des Steigungswinkels der Regressionsgeraden angibt. Der Regressionskoeffizient wird über die nachfolgende Formel ermittelt:
Verweise:
[1] Siehe Kapitel 3.5.3
3.5.4.1 Statistisch-mathematische Berechnung der linearen Regression
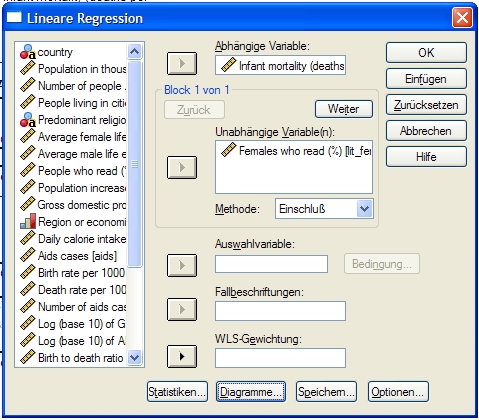
Die lineare Regression kann mit SPSS auf folgende Weise ermittelt werden:
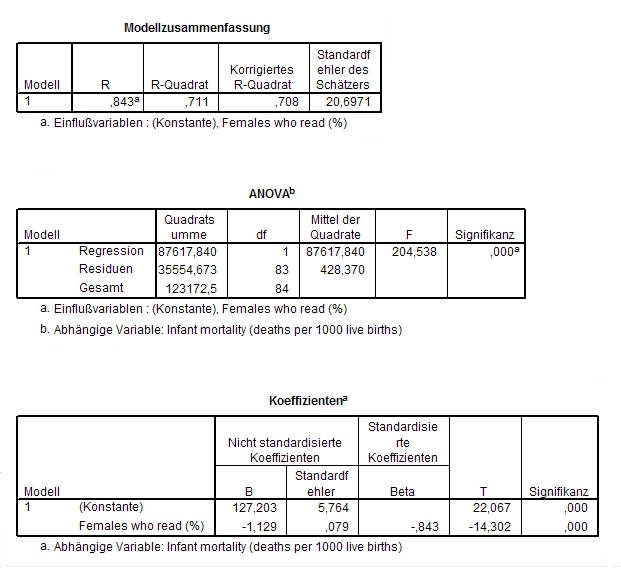
A. Klicken Sie auf ANALYSIEREN - REGRESSION - LINEAR. Es erscheint folgendes Fenster:
B. Tragen Sie in Abhängige Variable die von Ihnen gewünschte metrische Variable ein; in unabhängige Variable diejenige Variable, deren Einfluss auf die erste Variable Sie ergründen möchten.
C. Klicken Sie auf OK. Sie erhalten nun folgende Ausgaben:
Erklärungen:
Was in der ersten Tabelle R genannt wird, ist die Quadratwurzel aus dem Bestimmtheitsmaß und deckt sich bei der einfachen Regressionsanalyse mit dem Korrelationskoeffizienten[1] von Pearson. Die Korrelation von 0,711 ist durchaus ansehnlich.
Unter Koeffizienten stehen die zwei wesentlichen Werte für die Berechnung der Regressionsgerade: Die Konstante (hier 127,203) ist der Ausgangswert, der darunter stehende Wert -1,129 der Multiplikationsfaktor.
Die hier vorliegende Gleichung, die wir errechnen wollten, ist also:
A = -1,129*B + 127,203 oder in konkreten Begriffen formuliert:
Kindersterblichkeit (pro Tausend) = (weibliche Alphabetisierungsrate)*(-1,129) + 127,203
Bei einer weiblichen Alphabetisierungsrate von 50 % könnte man somit eine Kindersterblichratsrate von -1,129*50 + 127,203 voraussagen, also 70,753.
Es sei hinzugefügt, dass es sich hier nur um eine Einführung in die Regressionsanalyse handelt und deshalb auf wichtige damit zusammen hängende Begriffe wie Standardfehler der Schätzung nicht eingegangen werden kann.
Verweise:
[1] Siehe Kapitel 3.5.3.1
3.5.4.2 Grafische Darstellung der Regression
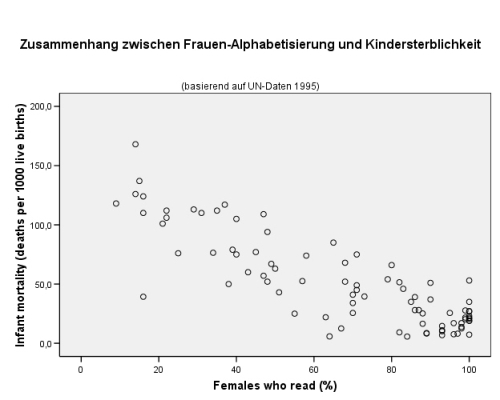
Grafisch kann man eine Regressionsgerade mit SPSS auf folgende Weise erstellen: Klicken Sie in der Menüleiste auf GRAFIKEN - STREU- /PUNKTDIAGRAMM - EINFACHES STREUDIAGRAMM. Dort geben Sie nach Klick auf Definieren in der Y- Achse eine metrische Variable ein, in der X-Achse genauso. Dann klicken Sie auf OK. Sie erhalten zuerst ein Streudiagramm, vorerst noch ohne Regressionsgerade:
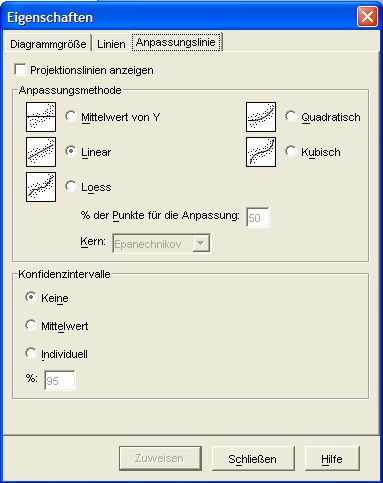
Nun machen Sie einen Doppelklick auf das Diagramm in der SPSS- Ausgabe. Sie landen im Diagramm-Editor. Unter Elemente können Sie Anpassungslinie bei Gesamtwert anklicken. Daraufhin wird defaultmäßig eine Regressionsgerade in das Streudiagramm eingefügt, gleichzeitig öffnet sich das folgende Fenster:
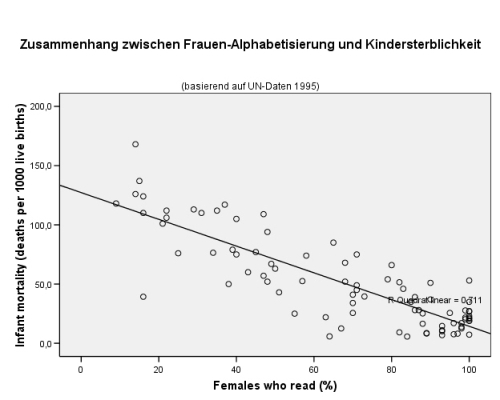
Kontrollieren Sie nochmals, ob hier Linear angeklickt ist. Nur linear realisiert eine Regressionsgerade. Nach Zuweisen erhalten Sie nun das Streudiagramm[1] mit der entsprechenden Regressionsgerade:
Verweise:
[1] Siehe Kapitel 3.6.1.6
Nächstes Kapitel: 3.6 Die grafische Darstellung statistischer Ergebnisse