Difference between revisions of "Ausgewählte statistische Grundlagen und Analysemethoden/Mittelwerte"
(Created page with " '''Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1 Notwendiges Wissen für die Wahl geeigneter statistischer Analysemethoden|Vorheriges Kapitel: 3.1 No...") |
(No difference)
|
Revision as of 16:34, 28 November 2019
Vorheriges Kapitel: 3.1 Notwendiges Wissen für die Wahl geeigneter statistischer Analysemethoden
Contents
3.2 Die Ermittlung von Häufigkeiten
verfasst von Erwin Ebermann
Bei der Ermittlung von Häufigkeiten stellen wir fest, wie oft die verschiedenen Messwerte auftreten.
Die Ermittlung von Häufigkeiten ist das einfachste statistische Verfahren und kann für jede Art von Skala[1] angewandt werden. Die Häufigkeiten der Messwerte geben uns Hinweise auf ihre Verteilung[2] d.h. wie oft die einzelnen Ausprägungen vorkamen. Die Kenntnis dieser Verteilung gibt uns somit Auskunft darüber, was in einer untersuchten Stichprobe der Normalfall, und was die Ausnahme ist.
Dabei wird das Auftreten von Werten gezählt. Prinzipiell unterscheiden wir zwischen
- Monovariablen Verteilungen: eine einzige Variable wird gezählt. So kommen wir z.B. zu Häufigkeiten von Schulnoten (22 SchülerInnen hatten eine 1, 37 eine 2 usw.)
- Bi- bzw. multivariablen Verteilungen: Es wird gezählt, wie häufig Kombinationen von zwei oder mehr Variablen auftreten (z.B. Schulnoten und soziale Schicht; 17 SchülerInnen gehörten zur Oberschicht und hatten eine 1, 22 SchülerInnen zur Oberschicht und hatten eine 2 etc.). Mit Bi- oder multivariablen Verteilungen möchte man Zusammenhänge zwischen zwei Variablen feststellen.
Die tabellarische Darstellung der Häufigkeiten in bi- bzw. multivariablen Verteilungen wird auch als Kreuztabelle[3] oder Kontingenztafel bezeichnet.
Nach der Systematik der Darstellung unterscheidet man zwischen der Urliste, der primären Tafel bzw. der Häufigkeitstabelle.
Verweise:
[1] Siehe Kapitel 3.1.2
[2] Siehe Kapitel 3.1.3
[3] Siehe Kapitel 3.5.2
Inhalt
3.2 Die Ermittlung von Häufigkeiten
3.2.1 Liste und Tafeln
3.2.2 Häufigkeitstabelle
3.2.2.1 Häufigkeitsberechnung mit SPSS
3.2.2.2 Grafische Darstellung mit SPSS
3.2.3 Klassenbildung (Gruppierung) von Daten
3.2.3.1 Gruppierung mit SPSS
3.2.4 Häufigkeitsdarstellung bei Mehrfachantworten mit SPSS
3.2.1 Liste und Tafeln
Urliste
Aufgenommene Messwerte sind anfangs ungeordnet. Denken Sie z.B. an 30 Personen, deren Alter Sie abgefragt haben, ohne die Einträge größenmäßig zu ordnen. Diese ungeordnete Liste wird als so genannte Urliste bezeichnet. Eine Urliste ist die ungeordnete Aufzählung der Werte in der gleichen Reihenfolge, in der sie während der Abfrage aufgenommen wurden.
Beispiel: Kinderzahl von Befragten
Primäre Tafel
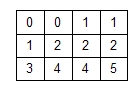
Wesentlich übersichtlicher ist bereits die primäre Tafel, in welcher die Ausprägungen sortiert werden. Sie gibt deutlich mehr Aufschluss über die Charakteristiken der Daten. Hier ist auf einen Blick erkennbar, dass die Messwerte 1 und 2 am häufigsten vorkommen:
Dennoch ist auch eine Primäre Tafel im Vergleich mit einer Häufigkeitstabelle wenig übersichtlich.
3.2.2 Häufigkeitstabelle
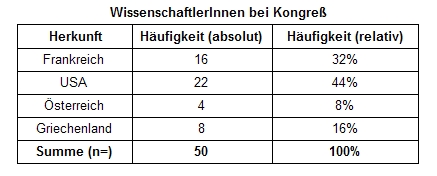
Häufigkeitstabellen zeigen in tabellarischer Form die Ausprägungen einer Variablen verbunden mit deren Häufigkeit. Sie sind weit übersichtlicher als Listen und Tafeln.
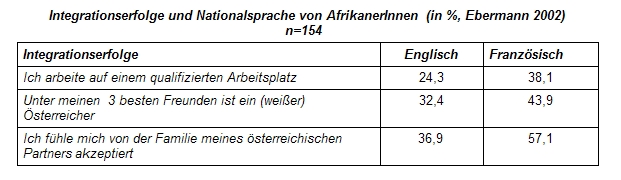
Dabei trägt man in der 1. Spalte die Messwerte ein (wie z.B. Kinderzahl oder hier Ländernamen), in der 2. Spalte die absolute Häufigkeit der Messwerte (durchzählen, wie oft z.B. Frankreich genannt wird) und in Spalte 3 berechnet man die relative Häufigkeit. Die relative Häufigkeit errechnet man folgendermaßen: man nimmt die absolute Häufigkeit eines Messwertes (z.B. waren 16 FranzösInnen beim Kongress), dividiert diesen durch die Summe der Messwerte (hier insgesamt 50 anwesende WissenschaftlerInnen) und multipliziert das Ergebnis mit 10 (um auf Prozentwerte zu kommen). Für FranzösInnen daher 16/50*100=32 %.Akkumulierte Häufigkeit
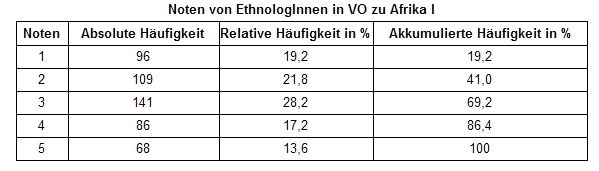
Wenn keine Nominalskalierung[1] vorliegt, ist auch die Darstellung der akkumulierten Häufigkeit sinnvoll. Sie gibt Auskunft über die Häufigkeit aller Messwerte, die bis zu einem bestimmten Niveau auftreten.
Man errechnet sie folgendermaßen: Man zählt alle relativen Häufigkeiten zusammen, die einschließlich dieser Zeile auftraten: Die akkumulierte Häufigkeit für die Note 3 (= alle EthnologInnen, die zumindest die Note 3 erhielten) wäre daher: 19,2 % + 21,8 % + 28,2 % = 69,2 %.
Eine derartige Häufigkeitstabelle kann, wie vorhin beschrieben, auch mehrdimensional sein (multivariabel):Eine Häufigkeitstabelle hat folgende Vorzüge:
- Sie ist übersichtlicher als eine Urliste
- Sie ist kürzer als eine primäre Tafel
- Sie ist ökonomisch
- Sie erlaubt eine leichte Beurteilung der Verteilung
- Trotz dieser Vorteile tritt kein Informationsverlust auf.
Verweise:
[1] Siehe Kapitel 3.1.2.2
3.2.2.1 Häufigkeitsberechnung mit SPSS
Die Berechnung von Häufigkeiten mit SPSS erfolgt folgendermaßen:
A. Klicken Sie in der Menüleiste auf ANALYSIEREN - DESKRIPTIVE STATISTIKEN - HÄUFIGKEITEN.
B. Fügen Sie im Feld Variablen die Variable ein, von der Sie eine Häufigkeitstabelle erstellen möchten.
C. Klicken Sie auf OK.
Sie erhalten dann z.B. folgende Ausgabe:
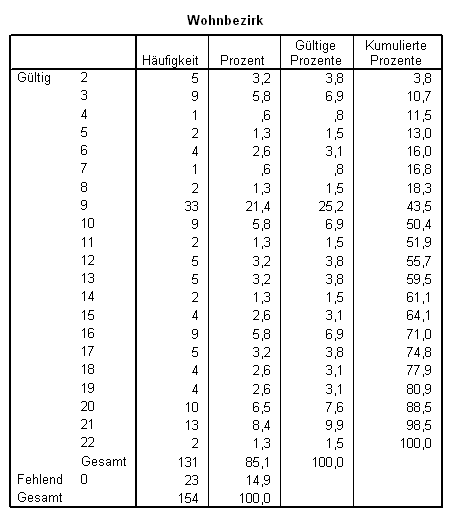
Sie sehen, dass SPSS in der ersten Spalte die Ausprägungen der Variable anbietet, in der Spalte Häufigkeit die absolute Häufigkeit, mit welcher diese Ausprägung auftritt. Unter Prozent finden Sie die prozentuellen Anteile der absoluten Häufigkeiten der Ausprägungen an der Stichprobengröße (N ist hier 154).
Links unten sehen Sie das Label Fehlend. Hier wird die Zahl der bei dieser Frage nicht vorhandenen Antworten vermerkt (Im Fall dieser Stichprobe haben 23 Personen diese Frage nicht beantwortet). Da daher die eigentliche Größe der Stichprobe bei 131 liegt (154 weniger 23 Nichtbeantwortende), verändern sich auch die realen Prozentwerte, wie in der Spalte Gültige Prozente ersichtlich. Die Spalte Kumulierte Prozente gibt die in Prozenten ausgedrückte akkumulierte Häufigkeit an und basiert ebenfalls auf den bereinigten Werten (also minus die Null- Einträge).
Bereits in der Standard-Vorgabe rechnet SPSS daher alle für eine Häufigkeitstabelle notwendigen Analysen. Werfen Sie auch einen Blick auf die fakultativen Auswahlmöglichkeiten unter Statistik und Diagramme. SPSS kann mit wenigen Arbeitsgängen äußerst umfangreiche Berechnungen durchführen.
3.2.2.2 Grafische Darstellung mit SPSS
Klicken Sie auf ANALYSIEREN - DESKRIPTIVE STATISTIK - HÄUFIGKEITEN und wählen Sie dort die Variable aus, deren Häufigkeitsverteilung Sie grafisch darstellen möchten.
Klicken Sie dann auf Diagramme. Sie haben nun die Auswahlmöglichkeit zwischen Balkendiagrammen[1], Kreisdiagrammen[2] und Histogrammen[3]. Je nach Datenlage sollten Sie unterschiedliche Diagrammtypen heranziehen. Siehe dazu den Punkt Diagramme[4].
Verweise:
[1] Siehe Kapitel 3.6.1.3
[2] Siehe Kapitel 3.6.1.1
[3] Siehe Kapitel 3.6.1.5
[4] Siehe Kapitel 3.6.2
3.2.3 Klassenbildung (Gruppierung) von Daten
Unter der Gruppierung von Daten verstehen wir die Zusammenfassung von verschiedenen Ausprägungen zu Klassen. Eine Klasse ist die Menge sämtlicher Messwerte, die innerhalb festgelegter Grenzen liegen. Dadurch kann die Häufigkeitsverteilung[1] einer Variablen mit einer Vielzahl unterschiedlicher Ausprägungen übersichtlicher dargestellt werden.
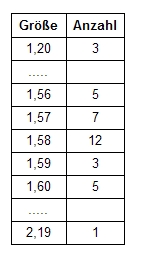
Beispiel: Gemessene Körpergrößen und Umwandlung in Klassen
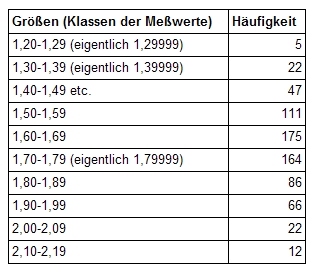
Ein Beispiel wären Größenangaben in cm. Wollte man statistische Aussagen über die Körpergrößen von ÖsterreicherInnen machen, müsste man wahrscheinlich (bei einem Alter ab 14) etwa 90 verschiedene Werte angeben (von 1,20 bis 2,19). Eine derartige Tabelle wäre unübersichtlich und würde über mehrere Seiten führen:
Die Klassenbreite ist bei diskreten Variablen[2] die Anzahl der in der Klasse zusammengefassten Messwerte. Berechnet wird sie mit: Höchster Wert der Klasse minus höchstem Wert der vorausgegangenen Klasse (hier also mit z.B. 1,89 m- 1,79 m= 0,10 m).
Die (exakten) Klassengrenzen (Intervallgrenzen) sind die kleinsten bzw. größten Messwerte einer Klasse (hier also z.B. 1,70 m und 1,79999 =1,8 m).
Bei richtiger Klassenbreite sollten keine leeren Klassen (Häufigkeit = 0) auftreten. Um Ausreißer mitbehandeln zu können, könnte man die untersten und obersten Klassen offen machen: z.B. „kleiner als 1,30 m“ statt „1,20-1,29 m“ bzw. „größer als 2,09 m“ statt „2,10-2,19 cm“.
Die Klassenmitte ist der Durchschnitt des kleinsten und des größten Wertes einer Klasse. Die Klassenmitte von 1,50-1,5999 periodisch wäre daher 1,55 m. Die Klassenmitte wird für spätere Berechnungen von Bedeutung sein (z.B. für Durchschnittsberechnungen).
Verweise:
[1] Siehe Kapitel 3.1.3
[2] Siehe Kapitel 3.1.1.2
3.2.3.1 Gruppierung mit SPSS
In vielen Fällen, besonders bei stetigen Variablen[1], wird die Zahl der Ausprägungen einer Variablen so groß sein, dass Häufigkeitsverteilungen[2] unübersichtlich werden. Im folgenden Beispiel wurde die Altersverteilung der Antwortenden abgefragt:
Es wäre deutlich übersichtlicher, diese Werte in eine kleine Zahl von Klassen umzukodieren. Dazu benützen Sie die Funktion TRANSFORMIEREN - UMCODIEREN[3] in der Menüleiste. Nun können Sie sich entscheiden zwischen einer Umcodierung in die gleiche oder in eine andere Variable. Es ist besser, sich für eine andere Variable zu entscheiden, da durch die Umcodierung (man kann auch mehrere Werte zu einem einzigen neuen umcodieren) Informationsverlust auftreten kann (ob willentlich oder durch einen Bedienungsfehler). Dieses Problem wird durch Umcodierung in eine neue Variable ausgeschlossen.
Sie wählen nun die Variable aus, welche umcodiert werden soll und geben im Feld Ausgabevariable einen neuen Namen dafür ein, der aus Gründen der Kompatibilität mit älteren Programmen acht Zeichen nicht überschreiten darf. Im Feld darunter können Sie jedoch einen beliebig langen und expressiveren Namen wählen.
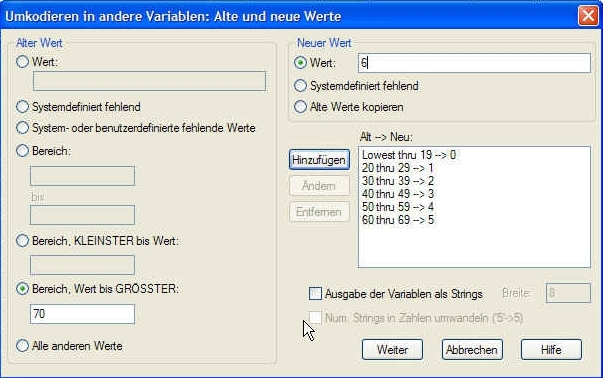
Klicken Sie nun auf Alte und neue Werte. Da Sie mehrere (numerische) Werte zu einem einzigen neuen zusammenfassen möchten, können Sie jeweils einen Bereich angeben (z.B. Bereich 20 bis 29), wenn Sie alle zwischen 20- 29jährigen in eine einzige Altersklasse ’zwischen 20 und 30 einbringen möchten’). Klicken Sie nach jeder einzelnen Angabe zur Umcodierung auf Hinzufügen. Für die unterste Klasse (alle unter 20jährigen wählen Sie Bereich, KLEINSTER bis Wert: (hier würden Sie 19 eingeben). Für die über 70jährigen bilden Sie eine offene Klasse, dazu wählen Sie Bereich, Wert bis GRÖSSTER: und geben hier 70 ein.
Klicken Sie am Ende auf Weiter und dann auf OK. Ihre Daten werden nun in die neue Variable umcodiert.
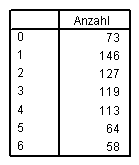
Die neue Häufigkeitstabelle sieht jetzt folgendermaßen aus:
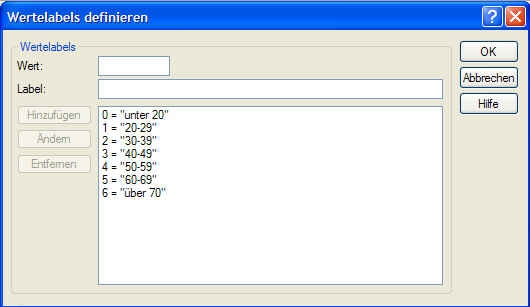
Nun müssen wir die neuen Werte, ausschließlich für die Ausgabe von SPSS, rückcodieren, um die Tabelle informativer zu machen, da wir nicht sofort erkennen können, dass 0 für ’unter 20’ steht. Damit SPSS intern mit den numerischen Daten rechnen kann, wir jedoch bei allen Ausgaben (Diagramme[4], Analysen etc.) informative Bezeichnungen erhalten, klicken wir in SPSS unten links auf die Variablenansicht. Im neuen Fenster finden wir bei der neuen Variable das Attribut Variablenlabel. Nach Doppelklick darauf erscheint folgendes Fenster:
Wir geben nun die gewünschten Labels für die numerischen Daten ein, also z.B. 20-29 für die Zahl 1 usw. Nach Eingabe aller automatisch durchzuführenden Änderungen klicken wir auf OK.
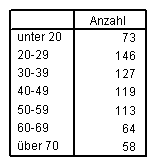
Wenn wir nun die gleiche Häufigkeitsberechnung wie oben durchführen, erhalten wir nun folgende leichter verständliche Tabelle:
Verweise:
[1] Siehe Kapitel 3.1.1.2
[2] Siehe Kapitel 3.1.3
[3] Siehe Kapitel 2.2.3.2
[4] Siehe Kapitel 3.6
3.2.4 Häufigkeitsdarstellung bei Mehrfachantworten mit SPSS
Falls Sie bei einer Frage explizit Mehrfachantworten zugelassen haben, können Sie deren Häufigkeiten mit SPSS komfortabel tabellarisch darstellen.
1. Definition eines Mehrfachantwortensets
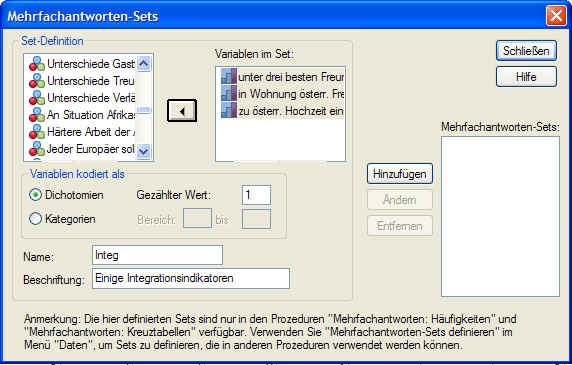
Sie müssen dazu zuerst ein (Mehrfachantworten-)Set definieren:
Klicken Sie in der Menüleiste auf ANALYSIEREN - MEHRFACHANTWORT - SET DEFINIEREN. Dann öffnet sich folgendes Fenster:
Führen Sie bitte folgende Schritte durch:
A. Sie wählen verschiedene dichotome Variable aus, die Sie in Variablen im Set einfügen;
B. Tragen Sie unter Gezählter Wert die Zahl 1 ein (d.h. dass jede Ja-Stimme einen Punkt zählt);
C. Sie lassen die Standardauswahl Dichotomien bei Variablen kodiert als;
D. Sie wählen einen Kurznamen (max. acht Zeichen für das Set) und tragen ihn unter Name ein;
E. Sie tragen unter Beschriftung einen längeren Namen ein, welcher die Tabelle anschaulich beschriften soll.
F. Klicken Sie nun auf Hinzufügen und letztendlich auf Schließen.
Das Set ist nun definiert, Sie können zur Analyse gehen:
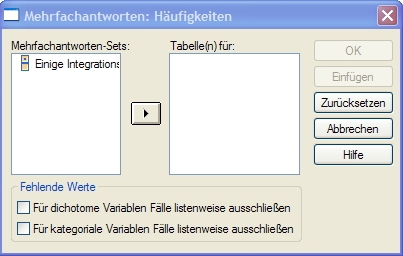
2. Analyse
A. Klicken Sie auf ANALYSIEREN - MEHRFACHANTWORT - HÄUFIGKEITEN. Das folgende Fenster öffnet sich:
B. Wählen Sie das Mehrfachantworten-Set, welches Sie angelegt haben und ziehen Sie es in das Feld Tabelle(n) für:
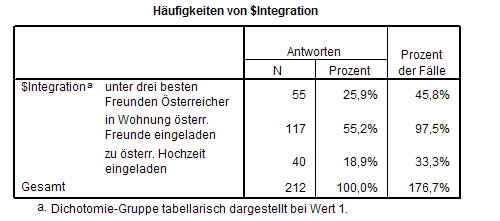
C. Klicken Sie auf OK. Die Analyse wird durchgeführt:
Nächstes Kapitel: 3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz