Difference between revisions of "Von der Fragestellung zur statistischen Analyse/Fehlerquellen"
(→Inhalt) |
m (Protected "Von der Fragestellung zur statistischen Analyse/Fehlerquellen" ([Edit=Allow only administrators] (indefinite) [Move=Allow only administrators] (indefinite)) [cascading]) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
'''[[Von_der_Fragestellung_zur_statistischen_Analyse/Gütekriterien#2.3 Gütekriterien quantitativer Untersuchungen|Vorheriges Kapitel: 2.3 Gütekriterien quantitativer Untersuchungen]]''' | '''[[Von_der_Fragestellung_zur_statistischen_Analyse/Gütekriterien#2.3 Gütekriterien quantitativer Untersuchungen|Vorheriges Kapitel: 2.3 Gütekriterien quantitativer Untersuchungen]]''' | ||
= 2.4 Fehlerquellen bei statistischer Arbeit = | = 2.4 Fehlerquellen bei statistischer Arbeit = | ||
| Line 8: | Line 6: | ||
Während '''Fehler der ersten und der zweiten Art''' zu nicht eliminarbaren Risiken der statistischen Arbeit gehören und auch bei sorgfältiger Herangehensweise nicht ausgeschlossen, sondern nur berücksichtigt werden können (siehe '''Irrtumswahrscheinlichkeit[[Funktion_und_Sinn_von_Statistik/Wahrscheinlichkeit#1.3.2 Irrtumswahrscheinlichkeit und Signifikanzniveau|[2]]]'''), hängen '''individuell bedingte Fehler''' mit Mängeln bei der Datenaufnahme, -übertragung oder Analyse zusammen. Wir könnten diese unter '''fehler-''' ''bzw.'' '''mangelhafte Daten''' zusammenfassen. | Während '''Fehler der ersten und der zweiten Art''' zu nicht eliminarbaren Risiken der statistischen Arbeit gehören und auch bei sorgfältiger Herangehensweise nicht ausgeschlossen, sondern nur berücksichtigt werden können (siehe '''Irrtumswahrscheinlichkeit[[Funktion_und_Sinn_von_Statistik/Wahrscheinlichkeit#1.3.2 Irrtumswahrscheinlichkeit und Signifikanzniveau|[2]]]'''), hängen '''individuell bedingte Fehler''' mit Mängeln bei der Datenaufnahme, -übertragung oder Analyse zusammen. Wir könnten diese unter '''fehler-''' ''bzw.'' '''mangelhafte Daten''' zusammenfassen. | ||
| − | |||
| Line 224: | Line 221: | ||
Nun tauchen in der ersten Zeile die leeren Antworten mit einer klaren und verständlichen Beschreibung auf. | Nun tauchen in der ersten Zeile die leeren Antworten mit einer klaren und verständlichen Beschreibung auf. | ||
| − | |||
| Line 230: | Line 226: | ||
[[Von_der_Fragestellung_zur_statistischen_Analyse/Operationalisierung#2.2.3 Vom Fragebogen zum Codeplan|[1] Siehe Kapitel 2.2.3]]<br /> | [[Von_der_Fragestellung_zur_statistischen_Analyse/Operationalisierung#2.2.3 Vom Fragebogen zum Codeplan|[1] Siehe Kapitel 2.2.3]]<br /> | ||
| + | <br /> | ||
'''[[Grundlagen_Statistischer_Auswertungsverfahren|↵ Zurück zur Übersicht]]''' | '''[[Grundlagen_Statistischer_Auswertungsverfahren|↵ Zurück zur Übersicht]]''' | ||
---- | ---- | ||
[[#2.4 Fehlerquellen bei statistischer Arbeit|↑ Nach oben]] | [[#2.4 Fehlerquellen bei statistischer Arbeit|↑ Nach oben]] | ||
Latest revision as of 14:31, 24 September 2020
Vorheriges Kapitel: 2.3 Gütekriterien quantitativer Untersuchungen
Contents
- 1 2.4 Fehlerquellen bei statistischer Arbeit
- 1.1 Inhalt
- 1.2 2.4.1 Fehler erster und zweiter Art
- 1.2.1 Hypothesen am Beginn der Untersuchung
- 1.2.2 Annahme oder Verwerfung von Hypothesen ist immer an Wahrscheinlichkeiten gebunden
- 1.2.3 Fehlerhafte Verwerfung bzw. Annahme von Hypothesen möglich
- 1.2.4 Mit der Zahl der statistischen Berechnungen steigt die Wahrscheinlichkeit von Fehlern der 1. oder 2. Art
- 1.2.5 Kontrolle durch qualitative Überlegungen erforderlich
- 1.3 2.4.2 Fehlerhafte oder mangelnde Daten
2.4 Fehlerquellen bei statistischer Arbeit
verfasst von Erwin Ebermann
Statistik ist der Versuch, aus einem Ausschnitt der Realität auf die Gesamtheit zu schließen. Dies bedeutet, dass unsere Aussagen über die (gesamte) Realität immer, ohne Ausnahme, mit einem Irrtumsrisiko behaftet sind, da wir nicht über vollständige Daten zur Grundgesamtheit[1] verfügen. Statistisch sprechen wir dabei von Fehlern der ersten und der zweiten Art.
Während Fehler der ersten und der zweiten Art zu nicht eliminarbaren Risiken der statistischen Arbeit gehören und auch bei sorgfältiger Herangehensweise nicht ausgeschlossen, sondern nur berücksichtigt werden können (siehe Irrtumswahrscheinlichkeit[2]), hängen individuell bedingte Fehler mit Mängeln bei der Datenaufnahme, -übertragung oder Analyse zusammen. Wir könnten diese unter fehler- bzw. mangelhafte Daten zusammenfassen.
Verweise:
[1] Siehe Kapitel 2.1
[2] Siehe Kapitel 1.3.2
Inhalt
2.4.1 Fehler erster und zweiter Art
Unter Fehler der ersten bzw. zweiten Art verstehen wir das systembedingte Problem, dass Hypothesen auch bei sorgfältigem Vorgehen fälschlich bestätigt oder verworfen werden.
Hypothesen am Beginn der Untersuchung
Bei Forschungsprojekten formulieren wir Hypothesen, deren Richtigkeit wir mit geeigneten Forschungs- und Analysemethoden untersuchen wollen. Eine derartige Ausgangshypothese oder Nullhypothese (in Kurzform oft auch H0 bezeichnet) könnte lauten: ’AfrikanerInnen werden am Arbeitsplatz weniger geschätzt als ChinesInnen.’.
Das Vorliegen einer Hypothese bedingt auch, dass es als Kontrast eine alternative Hypothese gibt (die wir bei der Erstellung des Konzepts als meist weniger wahrscheinlich einschätzen), die Alternativhypothese (in Kurzform oft auch H1 genannt). In unserem Fall könnte diese lauten: ’AfrikanerInnen werden am Arbeitsmarkt nicht weniger geschätzt als ChinesInnen.’.
Annahme oder Verwerfung von Hypothesen ist immer an Wahrscheinlichkeiten gebunden
Bei statistischen Analysen versuchen wir, Ergebnisse auf hohem Signifikanzniveau[1] zu erreichen. Wir sprechen davon, dass die gefundene Aussage mit einer Irrtumswahrscheinlichkeit von weniger als 5 %, weniger als 1 %, weniger als 1 ‰ zutrifft. Das bedeutet, dass unser Ergebnis, auf das wir so stolz sind, dennoch in 5 % aller Fälle, in 1 % aller Fälle etc. rein zufällig entstehen kann und, bei einer genügend häufigen Wiederholung, sogar muss.
Andererseits ist genauso denkbar, dass unser Ergebnis rein zufällig nicht den starken Zusammenhang zeigt, der normalerweise erscheint. Wir könnten auch bei großer Sorgfalt bei der Auswahl der Stichprobe überdurchschnittlich häufig auf Personen treffen, welche AfrikanerInnen besonders positiv gegenüber stehen.
Fehlerhafte Verwerfung bzw. Annahme von Hypothesen möglich
Es können also zwei verschiedene Fehler auftreten:
A. die Nullhypothese wird verworfen, obwohl sie richtig ist. Dies nennt man auch Fehler der ersten Art oder Alpha-Fehler;
B. die Nullhypothese wird angenommen, obwohl sie falsch ist. Dies bezeichnet man auch als Fehler der zweiten Art oder Beta-Fehler.
Mit der Zahl der statistischen Berechnungen steigt die Wahrscheinlichkeit von Fehlern der 1. oder 2. Art
Das Risiko, einem der beiden Fehler aufzusitzen, steigt natürlich mit der Höhe der Irrtumswahrscheinlichkeit sowie mit der Zahl der durchgeführten Analysen. Moderne PCs und Statistik-Software laden geradezu dazu ein, in kurzer Zeit tausende von Hypothesen zu überprüfen. Wenn wir 100 Variable miteinander kreuzen, erhalten wir (100x99)/2 Vergleiche, d.s. 4950 einzelne Untersuchungen auf signifikante Zusammenhänge. Wenn wir diese mit Chi-Quadrat-Tests auf dem 5 %-Irrtumsniveau untersuchen, erhalten wir im Normalfall 247,5 falsche Zusammenhänge (4950*0,05). Wir würden also in 247 Fällen einen Zusammenhang annehmen, obwohl er nicht vorhanden ist (Alpha-Fehler).
Kontrolle durch qualitative Überlegungen erforderlich
Derartige Massenvergleiche zeigen auch deutlich, dass statistische Berechnungen nicht losgelöst von qualitativen Überlegungen stattfinden dürfen. Bei statistischen Untersuchungen überraschend aufgetauchte Zusammenhänge müssen auch eine gewisse Stabilität und Systemkohärenz aufweisen, um akzeptiert werden zu können. D.h. sie müssen in einem gewissen Rahmen reproduzierbar sein und sie sollten nicht im Widerspruch zu offensichtlichen Fakten sein.
Verweise:
[1] Siehe Kapitel 1.3.2
2.4.2 Fehlerhafte oder mangelnde Daten
Fehler und Mängel können bei einer Reihe von Vorgängen bei statistisch unterstützten Forschungsprojekten erfolgen bzw. auftreten, wie z.B.:
A. Operationalisierungsfehler: bei der Operationalisierung[1] wurden verzerrende Messmethoden festgelegt;
B. Codierfehler: bei der Codierung[2] wurden, z.B. bei der Übertragung von Text-Daten in numerische Daten für interne Berechnungen von SPSS, Fehler begangen (z.B. die Vergabe des Zahlenwerts 4 in der Notenskala für ’Befriedigend’);
C. Interviewerfehler: bei der Datenaufnahme wurden fehlerhafte Werte eingetragen (z.B. eine Kinderzahl von 71 statt 7);
D. Widersprüchliche Datenlage: die Versuchspersonen oder die Datenquellen lieferten widersprüchliche Informationen, die sich in den Datenblättern wiederfinden;
E. Antwortverweigerung: verschiedene Fragen wurden von Versuchspersonen nicht beantwortet oder waren durch die Datenlage nicht erhebbar;
F. Eingabefehler: Datensätze wurden doppelt eingegeben;
G. Analysefehler: für die Analyse der Daten wurden die falschen Methoden[3] verwendet;
H. Interpretationsfehler: die Ergebnisse wurden richtig gerechnet, aber falsch interpretiert;
I. Grafiken[4] und Tabellen werden falsch oder ungenügend mit Zusatzinformationen versehen, was sowohl zu mangelndem Verständnis wie auch zu Nichtüberprüfbarkeit der Ergebnisse führen kann.
Verweise:
[1] Siehe Kapitel 2.2.1
[2] Siehe Kapitel 2.2.3.2
[3] Siehe Kapitel 3.1
[4] Siehe Kapitel 3.6.3
2.4.2.1 Eingabefehler
Meist werden Umfrageergebnisse zuerst handschriftlich aufgezeichnet. Danach werden die Daten in den PC übertragen, was mehrere potentielle Fehlerquellen berührt. Eine wenig leserliche Schrift kann zu Irrtümern bei der Eintragung in die Datenmatrix führen, genauso ’hängengebliebene Finger’ auf einer kleinen Tastatur, aber natürlich auch bewusste Falschangaben.
SPSS und Excel bieten verschiedene Möglichkeiten, die Eingabe von falschen Daten zu erschweren:
A. durch die Wahl geeigneter Datentypen
B. durch die Überprüfung, ob sich der eingetragene Wert innerhalb vorgegebener Grenzen befindet = Gültigkeitsprüfung.
2.4.2.1.1 Wahl geeigneter Datentypen mit SPSS
Verringerung des Risikos durch Wahl geeigneter Datentypen
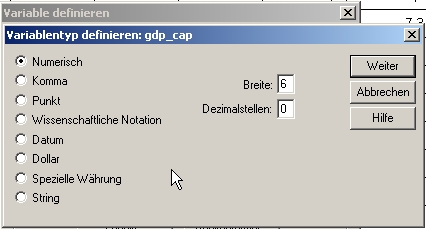
Besonders wichtig ist die richtige Definition des Datentyps (-> VARIABLENANSICHT - DATENTYP). In einem Stringfeld (oder Textfeld) können beliebige Zeichen stehen, in einem numerischen Feld nur Zahlen. Das bedeutet, dass durch Verschreiben keinerlei Buchstaben in ein numerisches Feld ’rutschen’ können. Der Datentyp kann jedoch noch wesentlich enger gefasst werden. Wenn ich im Feld Breite die Zahl 4 eintrage, kann ich z.B. bei numerischen Daten ausschließen, dass Jahreszahlen fehlerhaft durch Vertippen mit fünf Ziffern eingegeben werden. Gibt man bei Dezimalstellen 0 ein, sind nur ganze Zahlen möglich.
2.4.2.1.2 Gültigkeitsprüfung der Daten mit Excel
Unter Gültigkeitsprüfung von Daten versteht man die automatische Prüfung, ob aufgenommene Ausprägungen sich innerhalb eines vorgegebenen Bereichs befinden. Jeder außerhalb dieses Bereichs liegende Wert wird bei der Eingabe mit einer Fehlermeldung abgewiesen.
Für die meisten Variablen lassen sich mit geringer Sachkenntnis Ober- und Untergrenzen definieren, welche alle real auftretenden Ausprägungen umschließen. So könnte man bei der Aufnahme der Körpergröße von Erwachsenen eine Untergrenze von 80 cm und eine Obergrenze von 3 m annehmen; beim Lebensalter bei Erwachsenen eine Untergrenze von 18 und eine Obergrenze von 130; bei Schulnoten eine Untergrenze von 1 und eine Obergrenze von 5; beim Einkommen von Studierenden eine Untergrenze von 0 und eine Obergrenze von 4000 Euro.
Mit Excel geschieht dies folgendermaßen:
A. Man markiert die Spalte der Ausprägungen
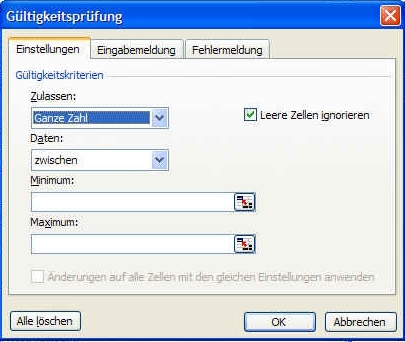
B. In der Menüleiste auf Daten und danach auf Gültigkeit klicken
C. Nun unter Zulassen Angabe des Datentyps machen. Wenn z.B. die Zahl der Kinder eingetragen werden sollte, würden wir hier Ganze Zahl wählen. Wählt man Liste aus, gelten alle Werte als gültig, welche sich in einer spezifischen Datei befinden (der Liste).
D. Unter Daten gibt man die Richtung der Ausprägungen an, also z.B. größer als, zwischen, ungleich etc. In unserem Fall der Kinderzahl wählen wir zwischen (auch größer oder gleich wäre denkbar).
E. Nun geben wir als Minimum-Wert ' die untere Begrenzung ein, in unserem Falle 0, da weniger Kinder nicht möglich sind und als Maximum in unserem Falle die Zahl 20 (kaum denkbar, dass jemand in Industrieländern eine höhere Kinderzahl aufweist).
F. Unter Eingabemeldung könnte man eine Meldung ausgeben lassen, welche bei Einträgen im Feld automatisch auf die Grenzen hinweist
G. Wichtiger ist es, unter Fehlermeldung anzugeben, warum ein eingetragener Wert als ungültig abgelehnt wird. Dazu wählen wir unter Typ eine bestimmte Signalform, in unserem Falle Warnung; danach geben wir unter Titel eine aussagekräftige Kurzmeldung und unter Fehlermeldung ausführlichere Erklärungen dazu ein.
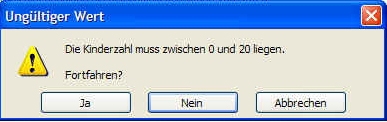
Falls wir nun in Excel in der betreffenden Spalte für Kinderzahlen die Ausprägung 22 eingeben, erhalten wir folgende Warnmeldung:
2.4.2.2 Doppelte Datensätze
Mitunter kann es geschehen, dass der gleiche Datensatz fehlerhafterweise doppelt eingegeben wird.
Doppelt eingegebene Datensätze kann man in SPSS mit folgender Funktion finden:
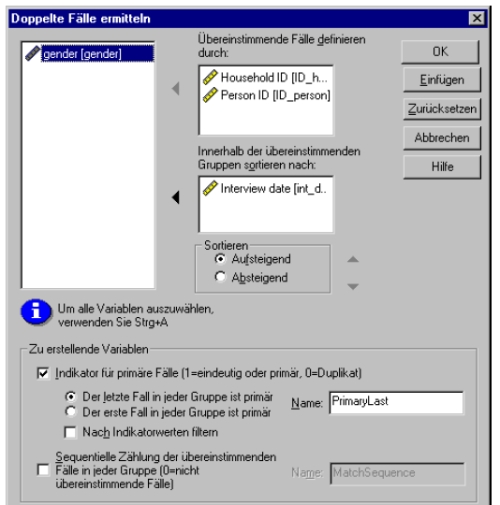
Klicken Sie auf DATEN - DOPPELTE FÄLLE ERMITTELN. Sie sehen folgendes Fenster:
Die wesentlichen Einträge hier sind:
A. Geben Sie unter Übereinstimmende Fälle definieren durch die Variablen an, welche zur Identifikation von Doppelgängern dienen. Das können normalerweise nur Variable sein, bei welchen Einträge eindeutig sein sollen (natürlich ist Eindeutigkeit auch durch eine Kombination mehrerer Variable erreichbar).
B. Sie können unter Innerhalb der übereinstimmenden Gruppen sortieren nach: noch eine Variable angeben, nach der sortiert werden soll.
Haben Sie somit doppelte Einträge gefunden, können Sie Fall für Fall entscheiden, wie Sie damit umgehen.
2.4.2.3 Fehlende Einträge
Was tun, wenn Einträge fehlen?
Nur bei den wenigsten Umfragen werden alle Fragen von allen Befragten beantwortet. Besonders tabuisierte Fragen wie vielleicht nach Bereichen der Sexualität, dem Einkommen, den politischen Neigungen werden oft nicht oder nur neutral beantwortet. Es stellt sich daher die Frage, ob und wie man die fehlenden Einträge interpretieren kann. Ein weiser Spruch der Kommunikationsforschung lautet: ’Man kann nicht nicht kommunizieren’ (Paul Watzlawick). Das bedeutet, dass vor allem bei tabusierten Fragen auch die Nichtbeantwortung von Fragen eine Information darstellt. Es könnte dementsprechend sein, dass bei manchen Fragen eine Nichtbeantwortung bedeutet: "Ich möchte nicht, dass man weiß, wie ich über diesen Bereich denke."
Beispiel: geringe Bekenntnisquote von FPÖ- WählerInnen
Viele Jahre lang hatten besonders FPÖ-WählerInnen während der Haider-Jahre große Angst, sich in Umfragen vor Wahlen zu ihrer Partei zu bekennen. Die Wahlergebnisse fielen daher für die FPÖ durch 1,5 Jahrzehnte stets wesentlich besser aus als die Umfrageergebnisse, was u.a. dazu führte, dass ihre Bekennerzahlen in Umfragen von den Meinungsforschungsinstituten einen substantiellen Zuschlag bekamen, um sich der tatsächlichen Unterstützung dieser Partei anzunähern.
Nichtbeantwortung auch durch Fehler möglich
In anderen, neutralen, Bereichen wird eine Nichtbeantwortung wieder eher als Übersehen oder als Ratlosigkeit (die Frage ist vielleicht unverständlich formuliert) gedeutet werden. Es gäbe kaum einen denkbaren Grund, die Frage nach seinem Lieblingsobst nicht zu beantworten.
Je nach Tabuisierungsgrad der Frage sind fehlende Einträge unterschiedlich aussagekräftig
Je nach Sachlage kann daher eine Nichtbeantwortung eine Art von Information oder einen Mangel darstellen. Im ersten Fall könnte es sein, dass z.B. besonders Personen, welche eine extrem abwehrende Haltung gegenüber MigrantInnen aufweisen (wie aus einer anderen Fragestellung erkennbar), besonders zur Nichtbeantwortung der Frage ’Welche Partei würden Sie wählen, wenn morgen Wahltag wäre?". Das heißt, dass wir uns bei auffallend häufiger Nichtbeantwortung von bestimmten Fragen die Frage stellen sollten, ob es bei den Nichtbeantwortenden gewisse Gemeinsamkeiten gibt und damit auch spezifische Motive der Nichtbeantwortung.
Wir müssen also bei der Behandlung der beiden Arten der Nichtbeantwortung differenzieren: im Falle der informationstragenden Nichtbeantwortung sollte der Antwort dennoch ein gewisser Wert beigemessen werden. Im Falle der informationsleeren Nichtbeantwortung sollten wir die Nichtantwort einfach aus der Gesamtzahl der möglichen Antworten ausschließen und dadurch die Stichprobengröße für diese Frage verkleinern.
2.4.2.3.1 Behandlung fehlender Daten mit SPSS
SPSS erlaubt, leere Felder automatisch mit bestimmten Einträgen auszufüllen oder dieselben in keinerlei Berechnungen einfließen zu lassen.
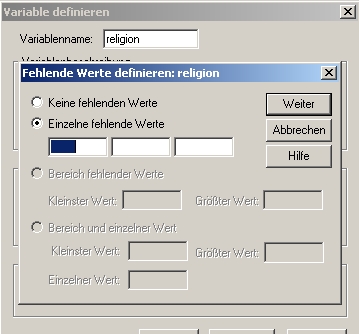
SPSS unterscheidet zwischen Systembedingt fehlenden Werten und Benutzerdefinierten fehlenden Werten. Werden z.B. Variable als numerisch definiert, werden leere Felder automatisch mit einem Komma in der Datenmatrix[1] markiert (Systembedingt). Bei Textfeldern muss ein fehlender Wert spezifisch deklariert werden (Benutzerdefinierter fehlender Wert):
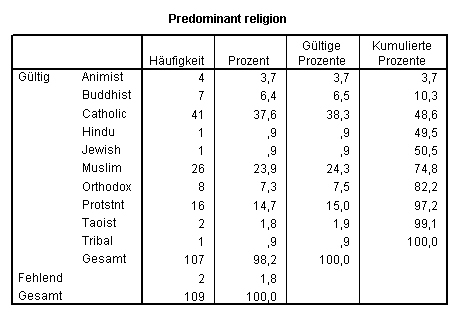
Man kann hier genau definieren, was als fehlender Wert gelten soll. Soll ein leeres Feld als solcher gelten, drückt man im ersten Feld von Einzelne fehlende Werte einmal auf die Leertaste. Man erhält hier in einem Beispiel die folgende Ausgabe:
Man erkennt, dass in der vorletzten Zeile 2 fehlende Werte eingetragen wurden. Auch die Größe der tatsächlich berücksichtigten Stichprobe hat sich um 2 verringert (siehe drittletzte Zeile).
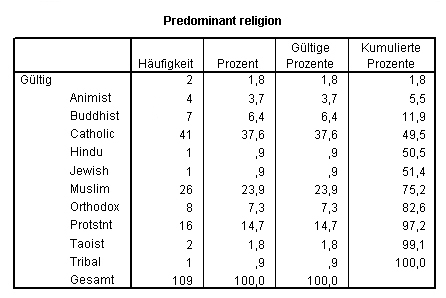
Falls man jedoch im Fenster Fehlende Werte definieren die Alternative Keine fehlenden Werte auswählt, erhalten Sie folgendes Ergebnis:
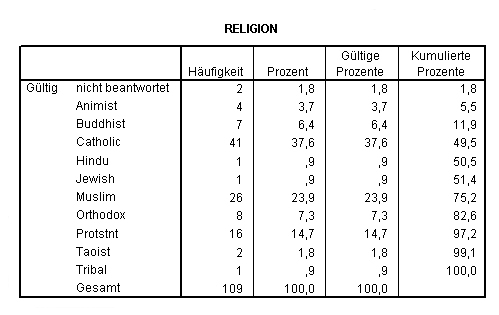
Die fehlenden Einträge in der vorletzten Zeile sind verschwunden, stattdessen findet sich in der ersten Zeile der ersten Spalte eine fehlende Beschreibung, neben der die Häufigkeit 2 steht. Die fehlenden Werte fließen hier voll in die Berechnung ein. Eine derartige leere Bezeichnung ist natürlich wenig anschaulich. Man muss sie daher für Bildschirm- und Printausgabe mit einer informativeren Beschreibung versehen. Dazu gehen wir wieder zur Variablenansicht und wählen in dieser (Variablen-)Labels aus.
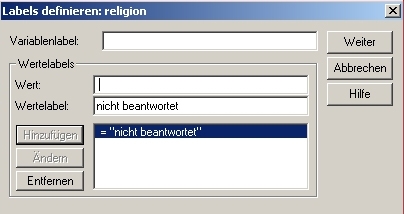
In Wert fügen wir wieder eine Betätigung der Pausetaste ein, unter Wertelabel z.B. ’nicht beantwortet’. Leerfelder werden dadurch deutlich informativer dargestellt, s.u.:
Nun tauchen in der ersten Zeile die leeren Antworten mit einer klaren und verständlichen Beschreibung auf.
Verweise:
[1] Siehe Kapitel 2.2.3