Von der Fragestellung zur statistischen Analyse/Operationalisierung

Vorheriges Kapitel: 2. Von der Fragestellung zur statistischen Analyse

2.1 Die Grundpopulation: worüber wir Aussagen machen

^{verfasst von Erwin Ebermann}

Die empirische Grundgesamtheit (Grundpopulation) ist jene abgegrenzte Menge von Personen (z.B. die Wiener Bevölkerung) oder Objekten (z.B. die Regenfälle in einer tropischen Region, die Autos im 7. Bezirk), über die man Aussagen machen möchte.

Anders ausgedrückt: Wenn wir eine Studie zu AfrikanerInnen in Österreich durchführen, dann möchten wir als Ergebnis zu Aussagen kommen, welche Tendenzen sich in dieser Bevölkerungsgruppe zeigen. Alle Mitglieder der Gruppe AfrikanerInnen in Österreich bilden gemeinsam die Grundgesamtheit.

Elemente, Variable und Ausprägungen

Ein Einzelobjekt aus dieser Grundgesamtheit bezeichnet man als statistische Einheit oder Element (z.B. Herr Moussa Bamba aus Bamako, der jetzt in Wien lebt). Die Einzelobjekte weisen jeweils Merkmale auf (auch Variablen genannt, z.B. Geschlecht, Einkommen, Autofarbe etc.), die uns interessieren und über deren Ausprägung in der Grundgesamtheit wir mehr erfahren möchten (die sogenannte Verteilung[1]). Die möglichen Werte dieser Merkmale bezeichnet man als Merkmalsausprägungen. So gibt es für das Merkmal Geschlecht die Ausprägungen männlich oder weiblich, für die Variable Körpergröße Zahlen zwischen theoretisch Null und deutlich über zwei Meter.

Befragung der gesamten Grundpopulation nur selten möglich

Meist ist die Grundpopulation so groß, dass wir nur einen Teil der Grundpopulation befragen können, eine sogenannte Stichprobe.

Öffentliche Quellen für Daten über Grundpopulationen

Grundinformationen über die Verteilung der Grundpopulationen kann man u.a. suchen bei Statistik Austria[2] und anderen Informationsstellen, in einschlägigen Publikationen etc.

Verweise:
[1] Siehe Kapitel 3.1.3
[2] http://www.statistik.at/

Inhalt

2.1 Die Grundpopulation: worüber wir Aussagen machen
2.1.1 Die Stichprobe (Sample)
2.1.2 Teil- oder Vollerhebung?
2.1.3 Die Ziehung (Auswahl) der Stichprobe
2.1.3.1 Geschichtete Stichprobenauswahl (Quotenstichprobe)
2.1.3.1.1 Proportional geschichtete Stichproben
2.1.3.1.2 Disproportional geschichtete Stichproben
2.1.3.1.3 Laufende Kontrolle der Schichtung
2.1.3.2 Zufallsstichproben
2.1.3.2.1 Einfache Zufallsstichprobe
2.1.3.2.2 Systematische Zufallsstichprobe
2.1.3.2.3 Geschichtete Zufallsstichprobe
2.1.3.3 Willkürliches Auswahlverfahren
2.1.3.4 Klumpenstichproben
2.1.4 Repräsentativität
2.1.5 Was tun, wenn die Grundpopulation nicht bekannt ist?

Weitere Kapitel dieser Lernunterlage

1. Funktion und Sinn von Statistik
3. Ausgewählte statistische Grundlagen und Analysemethoden
4. Software für quantitative Forschungsprojekte
5. Lexikon statistischer Grundbegriffe
6. Literatur, Ressourcen und Links

2.1.1 Die Stichprobe (Sample)

Eine Stichprobe ist eine Auswahl von Elementen der Grundgesamtheit, anhand derer die Grundgesamtheit[1] nachgebildet werden soll.

Auswahl fast immer notwendig

Auf Grund der Größe der Grundpopulationen ist es kaum jemals möglich, alle Mitglieder derselben zu befragen. Daher greift man in der Regel zu Stichproben, also einer Auswahl von Mitgliedern der Grundgesamtheit. Die Mitglieder der Stichproben sollten in der Regel so ausgewählt sein, dass sie ein unverzerrtes Abbild der Grundgesamtheit darstellen (siehe Repräsentativität[2]).

Verweise:
[1] Siehe Kapitel 2.1
[2] Siehe Kapitel 2.1.4

2.1.2 Teil- oder Vollerhebung?

Teil- oder Vollerhebung?

Je nach Größe der Grundpopulation, der Zahl der BefragerInnen und der finanziellen Ressourcen eines Forschungsprojekts kann eine Stichprobe unterschiedlich groß gewählt werden. Quantitativ sinnvolle Stichprobengrößen beginnen bei einer Befragtenanzahl von 100 und sind auch dann noch von großen Fehlermöglichkeiten gekennzeichnet. Sinnvoller wären auch hier deutlich höhere Stichprobengrößen. Wenn z.B. ein Meinungsforschungsinstitut die Wahlpräferenzen erhebt, befragt es in der Regel 300- 1000 Personen.

Falls die Grundpopulation relativ klein ist, wie z.B. ausländische HändlerInnen am Brunnenmarkt, lässt sich auch eine Vollerhebung durchführen. Dabei werden alle in Frage kommenden Personen befragt.

2.1.3 Die Ziehung (Auswahl) der Stichprobe

Unter Ziehung der Stichprobe versteht man die Selektion der Elemente der Stichprobe.

Die Formen der Ziehung der Stichprobe lassen sich prinzipiell unterteilen in

• Geschichtete Stichprobenauswahl
• Willkürliches Auswahlverfahren
• Zufallsstichproben
• Klumpenstichproben

---

2.1.3.1 Geschichtete Stichprobenauswahl (Quotenstichprobe)

Unter einer geschichteten Stichprobenauswahl versteht man ein Auswahlverfahren, bei dem wesentliche Verteilungscharakteristiken[1] der Grundgesamtheit[2] nachgebildet werden.

Einzelne für die Untersuchung als relevant erachtete Merkmale der Zielgruppe werden annähernd im gleichen Verhältnis auf die Stichprobe übertragen, wie sie in der Grundgesamtheit vorkommen.

Relevant sind besonders die Merkmale, welche bei der spezifischen Fragestellung zu besonderer Differenzierung führen können. Bei den Wahlpräferenzen sind das z.B. das Bundesland (Wien ist z.B. traditionell ein ’rotes’ Bundesland, NÖ ein ’schwarzes’); Geschlecht (Frauen haben oft ein ganz anderes Wahlverhalten als Männer); Alter (die Älteren haben eine stärkere Tendenz zur SPÖ, die Jüngeren zu den Grünen) etc.

Beispiel:
Man versucht die aktuellen Wahlpräferenzen der Österreicher mit insgesamt 500 Befragten zu erheben. Da etwa 1/5 der ÖsterreicherInnen in Wien lebt, sollte dementsprechend auch 1/5 der Befragten der Stichprobe, also ca. 100 Personen, aus Wien kommen, aber wesentlich weniger aus dem Burgenland. In gleicher Weise sollte auch die altersmäßige Verteilung der ÖsterreicherInnen wiedergegeben werden, also etwa 1/4 der Befragten über 60 Jahre etc.

Je nachdem, ob die wesentliichen Verteilungsparameter berücksichtigt werden oder einzelne teilweise bewusst verzerrt werden, spricht man von proportional geschichteten Stichproben oder von disproportional geschichteten Stichproben.

Verweise:
[1] Siehe Kapitel 3.1.3
[2] Siehe Kapitel 2.1

---

2.1.3.1.1 Proportional geschichtete Stichproben

Bei der proportional geschichteten Stichprobe werden die Schichten entsprechend ihrer Verteilung in der Grundgesamtheit ausgewählt. Es wird ein durchgehend treues und unverzerrtes Abbild der Grundgesamtheit angestrebt.

Besonders häufig werden für die Schichtung Geschlecht, Alter und Wohnart verwendet.

---

2.1.3.1.2 Disproportional geschichtete Stichproben

Unter einer disproportional geschichteten Stichprobe versteht man die bewusste Verzerrung einzelner Verteilungsparameter, um signifikante Aussagen über Randbereiche erhalten zu können. Dabei wird eine Bevölkerungsgruppe überproportional wiedergegeben, um genügend Interviews für sie zu erhalten.

Diese Methode wird v.a. angewandt, um bei beschränkten Stichprobengrößen signifikante[1] Aussagen über kleinere Bevölkerungsgruppen erhalten zu können, die für die Fragestellung besonders interessant sind.

Beispiel: Umfrage zu Reformen im Bildungsbereich

Problemstellung: Man möchte herausfinden, wie die österreichische Bevölkerung eine große Bildungsreform einschließlich des Hochschulwesens einschätzt. Man kann dabei insgesamt 1000 Personen befragen. Befragt man die österreichische Bevölkerung proportional geschichtet, würde man etwa 27 Studierende zu diesem Thema befragen, da mit etwa 220.000 Studierenden an öffentlichen Hochschulen ihr Anteil an der Bevölkerung bei ca. 2,7 % liegt. Man könnte somit bei bloß 27 befragten Studierenden keine verlässliche Aussage über sie bekommen, da ihre spezifische Anzahl zu klein ist. Da sie als Betroffene jedoch für die Fragestellung von besonderer Relevanz sind, könnte man sie übergewichten und 100 oder mehr von ihnen befragen.

Vorteil Kenntnis von Randbereichen, Nachteil Verzerrung des Meinungsbildes

Der Vorteil liegt in einer besseren Kenntnis des Meinungsbilds dieser thematisch wichtigen Subgruppe, der Nachteil dieser Methode in einem Verlust an Repräsentativität. Die Stichprobe ist verzerrt. Wollte man nun allgemeine Aussagen über das Meinungsbild bezüglich dieser Bildungsreform in der österreichischen Öffentlichkeit treffen, müsste man das Meinungsbild der Studierenden auf ihren tatsächlichen Anteil in der Bevölkerung hinuntergewichten.

Verweise:
[1] Siehe Kapitel 1.3.2

---

2.1.3.1.3 Laufende Kontrolle der Schichtung

Während der Befragungsphase laufende Kontrolle der Schichtung erforderlich

Bei einem quantitativen Forschungsprojekt führt man laufend Erhebungen, meist mit Fragebögen, durch. Dabei muss man stets einen Überblick über die Verteilung[1] der bereits Interviewten haben, um Abweichungen von der Verteilung in der Grundpopulation[2] korrigieren zu können. Wie? Indem man die nächsten Interviewten aus Personengruppen wählt, die bisher unterrepräsentiert waren, deren bisheriger Anteil in der Stichprobe also deutlich geringer als ihr Anteil in der Grundpopulation ist.

Berechnung

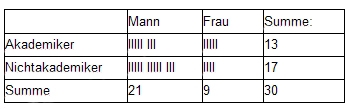
Bei ganz kleinen Umfragen kann man die Aufteilungsverhältnisse mit einer Matrix kontrollieren, in die man laufend mit ‚Stricherln’ einträgt, wen man interviewt hat. Nehmen wir an, in der Grundpopulation hätten wir eine Verteilung von 55 % Männern und 45 % Frauen bzw. von 25 % AkademikerInnen und 75 % NichtakademikerInnen. Mit den Schichtungsfragen stellen wir fest, ob die Verteilung der Interviewten mit der der Grundpopulation übereinstimmt. Daher müssen Schichtungsfragen auch fester Bestandteil der Fragebögen sein. Bisher haben wir folgende Interviews geführt:

Kontrolle der Aufteilungsverhältnisse in einer Matrix

In unserer Stichprobe findet sich bisher ein Männeranteil von 70 % (gegenüber 55 % in der Grundpopulation) sowie ein AkademikerInnen-Anteil von 43 % (gegenüber 25 % in der Grundpopulation). Daher müssen wir in Zukunft mehr Frauen und mehr NichtakademikerInnen befragen, solange, bis dieses Ungleichgewicht behoben ist. Zusätzlich gilt es zu bedenken, dass in unserer Stichprobe der Akademikeranteil bei den Männern bisher bei ca. 38 % liegt, der Akademikerinnen-Anteil bei den Frauen jedoch bei ca. 55 %. Sofern beide in der Grundpopulation den gleichen AkademikerInnen-Anteil aufweisen, müssten wir bei den folgenden Interviews darauf achten, dass bei Frauen noch stärker als bei den Männern besonders NichtakademikerInnen interviewt werden.

Verweise:
[1] Siehe Kapitel 3.1.3
[2] Siehe Kapitel 2.1

---

2.1.3.2 Zufallsstichproben

Unter Zufallsstichproben versteht man Auswahlverfahren einer Stichprobe, bei welchen bei einem theoretisch vorliegenden Register aller Elemente der Grundgesamtheit[1] die Elemente der Stichprobe zufällig gezogen werden.

Man vergleiche dies mit einer Lottoziehung. Man hat ein Register von 45 Lotto-Zahlen, welche die gleiche Ziehungwahrscheinlichkeit aufweisen. Aus diesen werden beim Lotto insgesamt sechs Zahlen gezogen.

Man unterscheidet zwischen einfachen und systematischen Zufallsstichproben. Eine Sonderform der Zufallsstichproben sind die geschichteten Zuallsstichproben.

Allgemeines Problem von Zufallsstichproben:

Es ist äußerst schwierig, Register aufzutreiben oder zu erstellen, welche tatsächlich jedem Element der Grundgesamtheit die gleiche Chance des Gezogenwerdens erlauben. Im Telefonregister scheinen viele Nummern nicht auf, da sie als Geheimnummern unterdrückt werden. Geheimnummern werden wiederum häufiger von besser etablierten Personen verwendet, weshalb sie über das Telefonregister eine geringere Chance haben, erreicht zu werden.

Verweise:
[1] Siehe Kapitel 2.1

---

2.1.3.2.1 Einfache Zufallsstichprobe

Bei der einfachen Zufallsstichprobe gibt es keinerlei Systematik der Ziehung.

Will man z.B. die Wiener Bevölkerung zum Thema Stadtautobahn befragen, könnte man alle Telefonnummern in einen PC einspeisen (das Register) und sich von einem Programm mit Zufallsgenerator 100 dieser Telefonnummern ’auswerfen’ lassen.

---

2.1.3.2.2 Systematische Zufallsstichprobe

Bei der systematischen Zufallsstichprobe erfolgt die Ziehung mit System, mit einem bestimmten Ziehungsschlüssel, und damit nicht mehr ganz zufällig.

Beispiel:
Man möchte die Einstellung der Wiener Bevölkerung zur Fristenlösung befragen. Man nimmt das Telefonbuch der Stadt Wien und wählt jede 100. Telefonnummer an.

Potentielle Probleme der systematischen Zufallsstichproben:

Ein Problem dieses Verfahrens kann in einer nicht erkannten Systematik der Verteilung liegen. Wenn man alle Personen befragt, welche jeweils die Türnummer 1 in den Häusern aufweisen, dann wäre die Wahrscheinlichkeit groß, dass Hausmeister deutlich überrrepräsentiert sind.

Systematik darf nicht zu starr sein:

Daher sollte die Systematik nicht zu starr sein. Man könnte z.B. bei der ersten Befragung im 1. Haus das Alter der Person abfragen und aus dem Alter die Türnummer des nächsten abzufragenden Hauses ermitteln, z.B. aus der Ziffernsumme. Nehmen wir an, ein Alter von 32 wird angegeben, dann ist die Ziffernsumme 3+2 = 5, beim nächsten Haus wird also die BewohnerIn der Türnummer 5 befragt usw.

---

2.1.3.2.3 Geschichtete Zufallsstichprobe

Eine Sonderform der Zufallsstichprobe ist die geschichtete Zufallsstichprobe. Bei dieser findet zuerst eine Einteilung der Stichprobe in sich nicht überlappende Schichten statt. Aus diesen werden wiederum einfache oder systematische Zufallsstichproben entnommen.

Beispiel: Befragung von WienerInnen

Man entscheidet sich zuerst für eine Berücksichtigung der Größenverhältnisse der einzelnen Bezirke, danach realisiert man mit der festgelegten Anzahl von Personen aus diesen Bezirken einfache oder systematische Zufallsstichproben.

---

2.1.3.3 Willkürliches Auswahlverfahren

Unter einem willkürlichen Auswahlverfahren versteht man eine unkontrollierte Form der Ziehung, bei welcher die Elemente der Grundgesamtheit eine deutlich unterschiedliche Wahrscheinlichkeit der Selektion aufweisen, weshalb von der Stichprobe nicht mehr auf die Grundgesamtheit geschlossen werden kann.

Beispiel:
Eine LehrerIn fragt in der Schule, welche SchülerInnen sich bereit erklären, bei einem sportlichen Ausdauertraining mit Vor- und Nachtest mitzumachen. Eine kleine Zahl von SchülerInnen meldet sich, die wahrscheinlich um einiges fitter als die anderen sind.

Sinnvoll für Rückschlüsse auf Methoden

Auch eine derartige Auswahl kann sinnvoll sein, wenn man z.B. messen möchte, ob sich die Fitness der ausgewählten TeilnehmerInnen durch das Training verbesserte. In der Medizin verwendet man oft dieses Auswahlverfahren, um die Wirksamkeit von Medikamenten zu testen.

Kein Rückschluss auf die Grundgesamtheit

Ein Rückschluss auf die Grundgesamtheit ist jedoch mit dem willkürlichen Auswahlverfahren nicht erlaubt.

---

2.1.3.4 Klumpenstichproben

Unter einer Klumpenstichprobe versteht man die Auswahl von Klumpen (Bündel von Erhebungselementen wie Schulklassen oder Unternehmen) nach dem Zufallsverfahren.

Dieses Auswahlverfahren erfolgt meist aus Gründen der Ökonomie. Statt einzelne SchülerInnen aus Schulen in 1000 Orten zu befragen, befragt man z.B. alle SchülerInnen aus 30 ausgewählten Orten, von denen man annimmt, dass diese bezüglich ihrer Eigenheiten die Grundgesamtheit der Orte abbilden.

2.1.4 Repräsentativität

Unter Repräsentativität versteht man die angestrebte Eigenschaft von statistischen Erhebungen, die Grundgesamtheit in der ausgewählten Stichprobe möglichst unverzerrt nachzubilden. Eine statistische Erhebung ist repräsentativ, wenn sie auf einer Zufallsstichprobe basiert und Aussagen über die Grundgesamtheit[1] zulässt.

Damit von der Stichprobe auf die Grundgesamtheit geschlossen werden kann, müssen bei den verschiedenen Formen der Ziehungen folgende Bedingungen erfüllt sein:

• Die Grundgesamtheit muss exakt definiert sein. Es muss somit klar festgelegt werden, welche Elemente zur Stichprobe gehören. Gehören z.B. bei einer Untersuchung über AfrikanerInnen in Österreich auch hier geborene Kinder von ZuwanderInnen zur Grundgesamtheit oder ausschließlich in Afrika Geborene?
• Die Grundgesamtheit muss physisch oder symbolisch präsent und manipulierbar sein (sie muss sich durchmischen lassen, jedes Element muss entnehmbar sein). Einfaches Beispiel: Bei einer Lottoziehung wären 45 Kugeln vorhanden, aus denen nach dem Zufallsprinzip jeweils eine gezogen wird.
• Jedes Element darf nur einmal in der Grundgesamtheit vertreten sein. Man darf also nicht z.B. die gleiche Person zweimal mit dem gleichen Fragebogen befragen.
• Die Auswahl muss so erfolgen, dass jedes Element die gleiche berechenbare Auswahlchance (größer 0) hat, in die Stichprobe zu gelangen. Wenn die Befragung ausschließlich an Orten oder zu Zeitpunkten stattfindet, an welchen ein Teil der Grundpopulation nicht oder nur selten erreichbar ist (z.B. ältere Menschen in Discos oder Arbeitende untertags im Park), dann ist die Repräsentativität ebenfalls nicht gewährleistet.

Verweise:
[1] Siehe Kapitel 2.1

2.1.5 Was tun, wenn die Grundpopulation nicht bekannt ist?

Sollte es unmöglich sein, statistische Daten über die Schichtung der Grundpopulation[1] zu erhalten, kann man entweder

• aufgrund vermutlich vergleichbarer Grundpopulationen verallgemeinern. Nehmen wir an, wir kennen den Frauenanteil von SudanesInnen in Wien nicht, Die ZuwanderInnen aus verschiedenen anderen vergleichbaren afrikanischen Ländern (islamisch, arabisch - englisch) weisen einen Frauenanteil von etwa 40 % auf, dann könnte man auch bei Sudanesinnen diesen Wert als Arbeitshypothese ansetzen. Man sollte jedoch unbedingt in der Publikation auf dieses Problem und die daraus folgende Annahme einer bestimmten Schichtung hinweisen.
• ExpertInnen zum Thema befragen, am besten gleich mehrere. Z.B. könnte man das Magistrat befragen, in welchem Ausmaß verschiedene Nationalitäten am Brunnenmarkt vertreten sind; IntegrationsforscherInnen, auch erfahrene Mitglieder der Grundpopulation etc.

Verweise:
[1] Siehe Kapitel 2.1

Nächstes Kapitel: 2.2 Die Operationalisierung

---

↑ Nach oben