Difference between revisions of "Von der Fragestellung zur statistischen Analyse/Operationalisierung"
(Created page with " '''Von_der_Fragestellung_zur_statistischen_Analyse#2. Von der Fragestellung zur statistischen Analyse|Vorheriges Kapitel: 2. Von der Fragestellung zur statistischen Analys...") |
|||
| Line 1: | Line 1: | ||
| − | + | '''[[Von_der_Fragestellung_zur_statistischen_Analyse/Grundpopulation#2.1 Die Grundpopulation: worüber wir Aussagen machen|Vorheriges Kapitel: 2.1 Die Grundpopulation: worüber wir Aussagen machen]]''' | |
| − | '''[[Von_der_Fragestellung_zur_statistischen_Analyse#2. | + | = 2.2 Die Operationalisierung = |
| − | = 2. | ||
<sup>verfasst von Erwin Ebermann</sup> | <sup>verfasst von Erwin Ebermann</sup> | ||
| − | + | Unter '''Operationalisierung''' versteht man die präzise Angabe der Vorgangsweise, mit der ein theoretisches Konstrukt gemessen werden soll (wie z.B. die Akzeptanz von Zuwanderergruppen). Dazu gehört die Auswahl der '''Indikatoren''', die genaue Formulierung der Fragen im '''Fragebogen''', dazu gehören die '''Antwortkategorien''', die Bestimmung der '''Messinstrumente''', die '''Bestimmung der Genauigkeit der Messung''', die '''Anweisungen an die InterviewerInnen''', wie sie die Fragen stellen und welche Zusatzinformationen sie geben dürfen etc. '''Operationalisierung[[Einige_wissenschaftstheoretische_Grundlagen_der_empirischen_Sozialforschung/Begriffe#2.7.1.1 Operationale Definition: Operationalisierung|[1]]]''' versucht also bis ins kleinste Detail sicherzustellen, dass die '''wissenschaftlichen Qualitätserfordernisse[[Von_der_Fragestellung_zur_statistischen_Analyse/Gütekriterien#2.3 Gütekriterien quantitativer Untersuchungen|[2]]]''' für vergleichbare Forschungsarbeiten eingehalten werden können und tatsächlich brauchbare Antworten zu den Themen gefunden werden können, die man zu untersuchen vorgibt. | |
| − | + | ==== '''Was man untersucht bzw. ’misst’, muss in seinen Ausprägungen in sinnvolle und voneinander abgrenzbare Untereinheiten unterteilt werden können.''' ==== | |
| − | + | Untersucht man z.B. die mathematischen Fähigkeiten von Schulkindern, kann man zur Notenskala greifen. Das Geschlecht kann in männlich und weiblich unterteilt werden. Bei der Untersuchung der Körpergröße wird man in Maßeinheiten wie cm oder mm messen. Die Einstellung gegenüber Zuwanderergruppen können wir z.B. in einer fünfteiligen Abstufung wiedergeben, wie z.B. ’sehr positiv’, ’eher positiv’, ’neutral’, ’eher ablehnend’ oder ’absolut ablehnend’. Den Erfolg bei den Bewerbungen von Zuwanderern am Arbeitsmarkt könnte man unterteilen in ’sofort abgelehnt’, ’zu Bewerbungsgespräch eingeladen, aber dann abgelehnt’ und ’aufgenommen’ unterteilen. Den Familienstand kann man in ’ledig’, ’geschieden’, ’verheiratet’, ’verwitwet’ unterteilen. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
'''Verweise:'''<br /> | '''Verweise:'''<br /> | ||
| − | [[ | + | [[Einige_wissenschaftstheoretische_Grundlagen_der_empirischen_Sozialforschung/Begriffe#2.7.1.1 Operationale Definition: Operationalisierung|[1] Siehe Kapitel 2.7.1.1 der Lernunterlage ''Einführung in die Empirischen Methoden der Kultur- und Sozialanthropologie'']]<br/> |
| − | [ | + | [[Von_der_Fragestellung_zur_statistischen_Analyse/Gütekriterien#2.3 Gütekriterien quantitativer Untersuchungen|[2] Siehe Kapitel 2.3]]<br /> |
==Inhalt== | ==Inhalt== | ||
<div class="eksa_toc"> | <div class="eksa_toc"> | ||
| − | [[Von_der_Fragestellung_zur_statistischen_Analyse/ | + | [[Von_der_Fragestellung_zur_statistischen_Analyse/Operationalisierung#2.2 Die Operationalisierung|2.2 Die Operationalisierung]]<br /> |
| − | [[Von_der_Fragestellung_zur_statistischen_Analyse/ | + | [[Von_der_Fragestellung_zur_statistischen_Analyse/Operationalisierung#2.2.1 Die Suche nach Indikatoren|2.2.1 Die Suche nach Indikatoren]]<br /> |
| − | [[Von_der_Fragestellung_zur_statistischen_Analyse/ | + | [[Von_der_Fragestellung_zur_statistischen_Analyse/Operationalisierung#2.2.2 Das Messen|2.2.2 Das Messen]]<br /> |
| − | [[Von_der_Fragestellung_zur_statistischen_Analyse/ | + | [[Von_der_Fragestellung_zur_statistischen_Analyse/Operationalisierung#2.2.2.1 Messfehler|2.2.2.1 Messfehler]]<br /> |
| − | + | [[Von_der_Fragestellung_zur_statistischen_Analyse/Operationalisierung#2.2.3 Vom Fragebogen zum Codeplan|2.2.3 Vom Fragebogen zum Codeplan]]<br /> | |
| − | + | [[Von_der_Fragestellung_zur_statistischen_Analyse/Operationalisierung#2.2.3.1 Dateneingabe und Erstellung einer Datenmatrix|2.2.3.1 Dateneingabe und Erstellung einer Datenmatrix]]<br /> | |
| − | [[Von_der_Fragestellung_zur_statistischen_Analyse/ | + | [[Von_der_Fragestellung_zur_statistischen_Analyse/Operationalisierung#2.2.3.2 Umcodierung mit SPSS|2.2.3.2 Umcodierung mit SPSS]]<br /> |
| − | [[Von_der_Fragestellung_zur_statistischen_Analyse/ | + | [[Von_der_Fragestellung_zur_statistischen_Analyse/Operationalisierung#2.2.3.3 Automatische Rückcodierung mit SPSS|2.2.3.3 Automatische Rückcodierung mit SPSS]]<br /> |
| − | [[Von_der_Fragestellung_zur_statistischen_Analyse/ | ||
| − | |||
| − | |||
| − | [[Von_der_Fragestellung_zur_statistischen_Analyse/ | ||
| − | |||
| − | |||
| − | |||
| − | |||
</div> | </div> | ||
| − | == | + | == 2.2.1 Die Suche nach Indikatoren == |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Im Forschungsentwurf werden verschiedene '''Hypothesen''' formuliert. Nun benötigt man eine Reihe von '''Indikatoren''', um die '''Hypothesen[[Einige_wissenschaftstheoretische_Grundlagen_der_empirischen_Sozialforschung/Begriffe#2.7.4 Hypothesen|[1]]]''' beibehalten bzw. verwerfen zu können. | |
| − | + | In vielen Fällen ist die Suche nach den '''Indikatoren''' einfach. Möchte man z.B. ermitteln, wie warm zur gleichen Jahreszeit verschiedene Orte sind, dann genügt eine Messung mit dem Thermometer. Meist jedoch sind die Forschungsfragen komplexer und nicht mit einer einzigen konkreten Messungsart zu beantworten. | |
| − | + | '''Beispiel 1:'''<br /> | |
| + | Nehmen wir an, Sie postulieren, dass die Gesellschaft in Nepal sehr ungleich und damit nicht egalitär ist. Nun bräuchten wir eine Reihe von sehr viel spezifischeren Fragestellungen, eigentlich '''Subhypothesen''', deren Synthese zur Beantwortung der allgemeinen Hypothese führen kann. Wir könnten zwischen materieller, rechtlicher und politischer (Un-)Gleichheit unterscheiden. Wir könnten Vermögensverhältnisse in verschiedenen Schichten betrachten; den Zugang zu staatlichen und privaten Ressourcen; wir könnten die Vertretung verschiedener Gruppen der Gesellschaft (Frauen, Adelige, Bauern etc.) im Parlament und anderen öffentlichen Gremien betrachten. Wir könnten die Schulbesuchsquote kontrastiv untersuchen etc. | ||
| + | In all diesen Punkten müssen wir äußerst konkret und präzise werden. Bezüglich des Schulbesuchs könnte man die Zahl der Jahre in der Schule, den maximalen Ausbildungsgrad etc. abfragen. Bezüglich des Vermögens Grundstücke, Häuser, Kapital, Vieh, andere Besitztümer, Leibeigene etc. Wir könnten Einschätzungen abfragen, ob Heiraten zwischen Adeligen und Nichtadeligen als akzeptabel empfunden werden, ob die Befragten annehmen, dass Arme und Reiche vor Gericht die gleichen Chancen haben usw. | ||
| + | '''Beispiel 2:'''<br /> | ||
| + | Sie nehmen an, dass viele Menschen in Wien AraberInnen ablehnen und oft sogar rassistisch gegenüberstehen. Sie könnten nun in einem Fragebogen an die Wiener Bevölkerung die Wertschätzung des Islams, der arabischen Kultur abfragen. Sie könnten fragen, in welchem Maße man annimmt, dass AraberInnen besonders leicht zu Terrorismus neigen. Sie könnten fragen, ob man sich vorstellen könnte, AraberInnen als angeheiratete Familienmitglieder zu akzeptieren. Sie könnten die Bereitschaft abfragen, AraberInnen Wohnungen zu vermieten. Sie könnten die Befragten ersuchen, die ersten Assoziationen zu nennen, die ihnen beim Begriff AraberInnen einfallen. Sie könnten die Befragten ersuchen, Ihnen das dominante Gefühl zu nennen, welches sie in Gegenwart von AraberInnen spüren usw. | ||
| − | + | Letztendlich könnte man sich auf einen Schlüssel einigen, mit welchem Anteil die mit den verschiedenen Detailfragen erhaltenen Informationen in einen Sammelparameter (Beispiel 1: Ungleichheit/Gleichheit; Beispiel 2: Rassismus gegenüber AraberInnen) einfließen. | |
| − | |||
| − | |||
| − | |||
| − | + | '''Verweise:'''<br /> | |
| − | + | [[Einige_wissenschaftstheoretische_Grundlagen_der_empirischen_Sozialforschung/Begriffe#2.7.4 Hypothesen|[1] Siehe Kapitel 2.7.4 der Lernunterlage ''Einführung in die Empirischen Methoden der Kultur- und Sozialanthropologie'']]<br/> | |
| − | |||
| − | + | == 2.2.2 Das Messen == | |
| − | + | Unter '''Messung''' versteht man die '''quantitative Bestimmung von Sachverhalten in Form einer Messgröße'''''.'' d.h. wir ordnen diesen Zahlen zu. | |
| + | Misst man die Temperatur eines Körpers, wird man in unseren Regionen in der Messgröße Celsius messen, in anderen in Fahrenheit etc. Messen wir die Körpergröße, dann messen wir bei größeren Körpern in Metern und Zentimetern, bei Kleinstlebewesen aber auch in Millionstel Metern und darunter. Messen wir das Haushaltseinkommen, werden wir in Euro messen. Bei der Messung von Einstellungen und sozialen Sachverhalten kann man selbst die Messgrößen bestimmen. So könnte man bei der Einschätzung der Sympathie für eine bestimmte Kultur fünf verschiedene Messgrößen festlegen, wie z.B. ’sehr sympathisch’, ’sympathisch’, ’neutral’, ’weniger sympathisch’ und ’unsympathisch’. | ||
| − | == | + | ==== '''Die Antwortkategorien müssen fair und ausgewogen sein''' ==== |
| − | + | Es wäre tendenziös und unseriös, in der obigen Sympathie-Skala im positiven Bereich nur ’sehr sympathisch’ anzugeben, im negativen jedoch die zwei vorhandenen Unterscheidungen. Dies könnte dazu führen, dass Antwortende, die nur eine leichte Sympathie für die andere Kultur empfinden, zum neutralen Wert ausweichen. Daher gilt als Grundregel, dass die Zahl der möglichen Antwortvarianten bei derartigen Fragen im negativen Bereich genauso hoch wie im positiven Bereich sein soll. | |
| − | + | Messungen beinhalten immer das Problem von '''Messfehlern'''. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
----- | ----- | ||
| − | === 2. | + | === 2.2.2.1 Messfehler === |
| − | Unter | + | Unter '''Messfehler''' versteht man die Abweichung des Ergebnisses von Messungen von den realen Gegebenheiten. Wo eine Messung erfolgt, sollte man immer die Möglichkeit von Messfehlern berücksichtigen. Man kann zwischen '''zufälligen''', '''systematischen und fahrlässigen Messfehlern''' unterscheiden. |
| − | + | ==== '''A. Zufällige Messfehler:''' ==== | |
| − | + | Zufällige Messfehler sind von den Messenden nicht zu kontrollieren. Wenn man zum Beispiel eine bestimmte Personengruppe zu einem sensiblen Thema befragen möchte und gerade am Tag vorher ein (den InterviewerInnen unbekanntes) Ereignis eintritt, welches ihre Neigung zu ehrlichen Antworten temporär verändert, während bei Vergleichsgruppen im gleichen Zeitraum nichts Vergleichbares auftritt, können verfälschte Ergebnisse auftreten. Misst man die Regenfälle in der Sahelgegend, kann es sein, dass ein Ort deutlich besser und gleichmäßiger beregnet wird, als die nicht gemessenen Nachbarorte, im nächsten Jahr kann es umgekehrt sein. Es gibt jedoch einen sogenannten '''Zentralen Grenzwertsatz der Statistik (Wikibooks)[https://de.wikibooks.org/wiki/Statistik:_Zentraler_Grenzwertsatz [1]]''', nach welchem zufällige Fehler sich im Laufe der Zeit ausgleichen und einer Normalverteilung zustreben. Man kann daher postulieren, dass die zufälligen Messfehler bei häufigen Messungen zum Ausgleich tendieren. | |
| − | ''' | + | ==== '''B. Systematische Messfehler:''' ==== |
| − | |||
| − | + | Systematische Messfehler können durch '''fehlerhafte Messgeräte''' entstehen, wie z.B. die Gewichtsmessung durch eine verstellte Waage; die Zeitmessung durch eine ungenaue Uhr; aber auch z.B. eine Kommunikationsform, welche den Zugang zu manchen Informationen kaum erlaubt. So ist es möglich, dass besonders hoch emotionale Angelegenheiten in einer Fremdsprache zu anderen Antworten als in seiner Muttersprache führen. Man überlege sich, ob es einem in einer Fremdsprache ähnlich schwer wie in seiner Muttersprache fällt, z.B. ''Ich liebe Dich'' zu sagen, wo beim Aussprechen ähnlicher Sätze auch Assoziationen mit Enttäuschungen u.a. verbunden sein können und damit auch die Angst vor Zurückweisung. | |
| + | Ein Teil der systematischen Messfehler kann durch '''stetige Kontrolle''' und '''kritische Hinterfragung''' der Messinstrumente behoben werden. | ||
| + | ==== '''C. Fahrlässige Messfehler:''' ==== | ||
| − | ''' | + | '''Grobe Messfehler''' '''beruhen auf menschlichen Fehlern'''. Man trägt z.B. beim Alter 15 statt 51 ein, schreibt eine Antwort in die falsche Spalte; vergisst eine Frage zu stellen oder zu beantworten. Man vermittelt beim Interview eigene Einstellungen, welche mit großer Wahrscheinlichkeit zu einer veränderten Reaktion des Befragten führen (wenn man z.B. einem Befragten deutlich zeigt, dass man seine Einstellungen und Meinungen geringschätzt). |
| − | |||
| − | |||
| + | Weiterführendes zu Messfehlern: | ||
| − | + | '''Messfehler (Wikipedia)[http://de.wikipedia.org/wiki/Messfehler [2]]''' | |
| − | |||
| − | |||
| − | + | '''Verweise:'''<br /> | |
| + | [https://de.wikibooks.org/wiki/Statistik:_Zentraler_Grenzwertsatz [1] https://de.wikibooks.org/wiki/Statistik:_Zentraler_Grenzwertsatz]<br /> | ||
| + | [http://de.wikipedia.org/wiki/Messfehler [2] http://de.wikipedia.org/wiki/Messfehler]<br /> | ||
| − | + | == 2.2.3 Vom Fragebogen zum Codeplan == | |
| − | + | Unter einem '''Codeplan''' verstehen wir die '''Auflistung aller verwendeten Variablen''' mit einer eindeutigen Information zur inhaltlichen Bedeutung der numerischen Codes, eventuell noch von weiteren Informationen begleitet, welche sich auf den Messvorgang beziehen. | |
| − | + | In einem Codeplan halten wir eindeutig fest, '''welchen Variablennamen Fragen des Fragebogens entsprechen''', '''wie verschiedene Ausprägungen von Variablen gemessen werden''' (z.B. in cm für die Körpergröße oder in Ja/Nein für bestimmte Erfahrungen) und '''wie diese Ausprägungen in eine numerische Form übersetzt werden''', was überhaupt erst eine maschinelle quantitative Analyse erlaubt. | |
| − | + | ==== '''Statistikprogramme benötigen automatisch interpretierbare Datentypen''' ==== | |
| − | + | Statistikprogramme benötigen für Berechnungen bestimmte Datentypen, die in der Regel '''numerisch''' sind. Kein Statistikprogramm kann in den Antwortkategorien ’sehr’, ’eher schon’, ’durchschnittlich’, ’eher weniger’, ’überhaupt nicht’ eine logische Reihe erkennen, dass also diese Bezeichnungen für verschiedene logische Abstufungen stehen, nämlich für eine '''Ordinalskala[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.2.3 Ordinalskalierung|[1]]]'''. | |
| − | + | Damit ein Statistikprogramm wie '''SPSS''' die logische Reihenfolge erkennen und danach Analysen über diese bilden kann, müssen die Textwerte in numerische umcodiert werden. Im '''Codeplan''', d.h. der Dokumentation über die ursprünglichen Text- Begriffe und ihrer numerischen Entsprechungen, werden diese Umcodierungen festgehalten. Im obigen Beispiel könnte man ’sehr’ immer durch 1, ’eher schon’ durch 2, ’durchschnittlich’ durch 3, ’eher weniger’ durch 4 und ’überhaupt nicht’ durch 5 ersetzen. Nun ist eine für die Software durchgehende Reihe von 1-5 entstanden, die vom kleinsten zum größten Wert gereiht ist. | |
| − | + | Aktuelle Statistikprogramme wie '''SPSS''' rechnen intern mit diesen numerischen Daten, können mit einfachen Befehlen jedoch bei der Ausgabe der Ergebnisse automatisch die urspünglichen Textinformationen verwenden. | |
| − | + | Beispiel eines Codeplans: | |
| − | + | [[File:quantitative-30_1.jpg|frame|center|Beispiel eines Codeplans]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[File:quantitative- | ||
| − | |||
| − | |||
'''Verweise:'''<br /> | '''Verweise:'''<br /> | ||
| − | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.3 | + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Eignung#3.1.2.3 Ordinalskalierung|[1] Siehe Kapitel 3.1.2.3]]<br /> |
| − | |||
----- | ----- | ||
| − | === 2. | + | === 2.2.3.1 Dateneingabe und Erstellung einer Datenmatrix === |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Unter einer '''Datenmatrix''' versteht man eine '''Tabelle, in welcher alle Messungen an den Versuchsobjekten zusammengefasst werden'''. Die Daten sind normalerweise so angeordnet, dass jede Zeile der Datenmatrix alle '''Messungen''' an einem einzelnen Datenobjekt enthält. In den Zeilen stehen somit von links nach rechts die Angaben zu einer Person (bzw. zu den Untersuchungsobjekten), während in den Spalten die Variablen eingetragen werden. | |
| + | Siehe z.B. die ersten Spalten und Zeilen der SPSS-Datei zur weltweiten Entwicklung world95.sav: | ||
| + | [[File:quantitative-31_1.jpg|frame|center|Beispiel einer SPSS-Datenmatrix]] | ||
| + | Die Untersuchungsobjekte sind hier eindeutig durch ihre in der ersten Spalte stehenden (Länder-)Namen identifiziert. Von links nach rechts werden danach in den einzelnen Zeilen durch Variable Informationen zu den jeweiligen Ländern angegeben: Bevölkerungsgröße, Bevölkerungsdichte, Prozentsatz der städtischen Bevölkerung, Religion etc. | ||
| − | + | Es ist äußerst empfehlenswert, die Datenmatrix in der hier beschriebenen Weise zu verwalten, da alle führenden und gängigen Analyse- und Darstellungsprogramme (Excel, SPSS etc.) die gleiche Anordnung verwenden. | |
| − | |||
----- | ----- | ||
| − | === 2. | + | === 2.2.3.2 Umcodierung mit SPSS === |
| − | + | SPSS benötigt gleichzeitig für viele Funktionen numerische Daten, wo Daten in ''String'' (oder Text-)Format vorliegen. So kann SPSS bei reinen Textdaten, wie z.B. ’Sehr Gut’ oder ’Gut’ nicht erkennen, dass ’Sehr Gut’ eine höhere Intensität bzw. Qualität als ’Gut’ wiederspiegelt. SPSS würde eine sinnvolle Rangfolge jedoch in numerischer Form erkennen. | |
| − | + | SPSS erlaubt es, '''Stringvariable''' automatisch in '''numerische''' zu codieren. | |
| + | Dazu benützen Sie die Funktion TRANSFORMIEREN - UMCODIEREN in der Menüleiste. Nun können Sie sich entscheiden, ob die Umcodierung in die gleiche oder in eine andere Variable erfolgen soll. Es ist besser, sich für ''eine andere Variable'' zu entscheiden, da durch die Umcodierung (man kann auch mehrere Werte zu einem einzigen neuen umcodieren) Informationsverlust auftreten kann (ob willentlich oder durch einen Bedienungsfehler). Dieses Problem wird durch Umcodierung in eine neue Variable ausgeschlossen. | ||
| − | + | Sie wählen nun die Variable aus, welche umcodiert werden soll und geben im Feld Ausgabevariable einen neuen Namen dafür ein (der aus Gründen verschiedenster Kompatibilität) acht Zeichen nicht überschreiten darf. Im Feld darunter können Sie jedoch einen beliebig langen und expressiveren Namen wählen. | |
| − | + | [[File:quantitative-32_1.jpg|frame|center|Umkodieren in andere Variablen mit SPSS]] | |
| + | Klicken Sie nun auf ''Alte und neue Werte''. Wenn Sie einzelne Werte umcodieren möchten, geben Sie im Feld ''Wert'' denselben ein (z.B. Matura). Nun benötigen Sie einen neuen Wert dafür. Dafür könnten Sie z.B. die Zahl 3 im Feld ''Neuer Wert'' eingeben. Im oben angeführten Beispiel wären verschiedene abgeschlossene Ausbildungsstufen in eine logische Reihenfolge gebracht. | ||
| − | + | Falls Sie mehrere (numerische) Werte zu einem einzigen neuen zusammenfassen möchten, können Sie einen Bereich angeben (z.B. ''Bereich'' 20 ''bis'' 29), wenn Sie alle zwischen 20-29jährigen in eine einzige Altersklasse ’zwischen 20 und 30' einbringen möchten). Klicken Sie nach jeder einzelnen Angabe zur Umcodierung auf ''Hinzufügen.'' | |
| − | ''' | + | Klicken Sie am Ende auf Weiter und dann auf OK. Ihre Daten werden nun in die neue Variable umcodiert. Erst jetzt wäre es Ihnen möglich, dass SPSS die Ausbildung nach Jahren und Qualität sinnvoll reihen kann und natürlich auch viele weitere (damit zusammenhängenden) Analysen rechnen kann. So wäre erst jetzt die Berechnung einer '''Korrelation[[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3 Die Korrelation|[1]]]''' zwischen dem Ausbildungsgrad und dem Einkommen möglich. |
| − | |||
| − | |||
| − | |||
| − | + | '''Verweise:'''<br /> | |
| − | + | [[Ausgewählte_statistische_Grundlagen_und_Analysemethoden/Korrelation#3.5.3 Die Korrelation|[1] Siehe Kapitel 3.5.3]]<br /> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
----- | ----- | ||
| − | === 2. | + | === 2.2.3.3 Automatische Rückcodierung mit SPSS === |
| − | + | Damit SPSS mit Daten rechnen kann, wurden diese in numerischer Form eingegeben oder in eine neue numerische Variable umcodiert. Wenn Sie nun eine auf diesen neuen Variablen basierende Analyse starten, wirken die Ergebnisse ohne zusätzliche Information wenig informativ. | |
| − | + | [[File:quantitative-33_1.gif|frame|center|Numerische Variablen]] | |
| + | Niemand könnte ohne Zusatzinformation wissen, dass ''0'' für ''Nein'' und ''1'' für ''Ja'' steht. Damit SPSS intern mit den numerischen Daten rechnen kann, wir jedoch bei allen Ausgaben (Diagramme, Analysen etc.) informative Bezeichnungen erhalten, klicken wir in SPSS unten links auf die ''Variablenansicht.'' Im neuen Fenster finden wir in der Zeile der neuen Variable den Punkt ''Variablenlabel.'' Nach Doppelklick darauf erscheint folgendes Fenster: | ||
| − | + | [[File:quantitative-33_2.jpg|frame|center|Definition der Wertelabels mit SPSS]] | |
| − | + | Wir geben nun für den Wert das gewünschte Label ein. Wir möchten, dass statt ''0'' der aussagekräftige Text ''Nein'' erscheint, statt ''1'' der aussagekräftige Wert ''Ja.'' Nach Eingabe aller automatisch durchzuführenden Änderungen klicken wir auf OK. | |
| − | + | Wenn wir nun die gleiche Häufigkeitsberechnung wie oben durchführen, erhalten wir nun folgende leichter verständliche Tabelle: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[File:quantitative-33_3.gif|frame|center|Tabelle mit Wertelabels]] | ||
<br /> | <br /> | ||
| − | '''[[Von_der_Fragestellung_zur_statistischen_Analyse/ | + | '''[[Von_der_Fragestellung_zur_statistischen_Analyse/Gütekriterien#2.3 Gütekriterien quantitativer Untersuchungen|Nächstes Kapitel: 2.3 Gütekriterien quantitativer Untersuchungen]]''' |
---- | ---- | ||
| − | [[#2. | + | [[#2.2 Die Operationalisierung|↑ Nach oben]] |
Revision as of 16:44, 28 November 2019
Vorheriges Kapitel: 2.1 Die Grundpopulation: worüber wir Aussagen machen
Contents
2.2 Die Operationalisierung
verfasst von Erwin Ebermann
Unter Operationalisierung versteht man die präzise Angabe der Vorgangsweise, mit der ein theoretisches Konstrukt gemessen werden soll (wie z.B. die Akzeptanz von Zuwanderergruppen). Dazu gehört die Auswahl der Indikatoren, die genaue Formulierung der Fragen im Fragebogen, dazu gehören die Antwortkategorien, die Bestimmung der Messinstrumente, die Bestimmung der Genauigkeit der Messung, die Anweisungen an die InterviewerInnen, wie sie die Fragen stellen und welche Zusatzinformationen sie geben dürfen etc. Operationalisierung[1] versucht also bis ins kleinste Detail sicherzustellen, dass die wissenschaftlichen Qualitätserfordernisse[2] für vergleichbare Forschungsarbeiten eingehalten werden können und tatsächlich brauchbare Antworten zu den Themen gefunden werden können, die man zu untersuchen vorgibt.
Was man untersucht bzw. ’misst’, muss in seinen Ausprägungen in sinnvolle und voneinander abgrenzbare Untereinheiten unterteilt werden können.
Untersucht man z.B. die mathematischen Fähigkeiten von Schulkindern, kann man zur Notenskala greifen. Das Geschlecht kann in männlich und weiblich unterteilt werden. Bei der Untersuchung der Körpergröße wird man in Maßeinheiten wie cm oder mm messen. Die Einstellung gegenüber Zuwanderergruppen können wir z.B. in einer fünfteiligen Abstufung wiedergeben, wie z.B. ’sehr positiv’, ’eher positiv’, ’neutral’, ’eher ablehnend’ oder ’absolut ablehnend’. Den Erfolg bei den Bewerbungen von Zuwanderern am Arbeitsmarkt könnte man unterteilen in ’sofort abgelehnt’, ’zu Bewerbungsgespräch eingeladen, aber dann abgelehnt’ und ’aufgenommen’ unterteilen. Den Familienstand kann man in ’ledig’, ’geschieden’, ’verheiratet’, ’verwitwet’ unterteilen.
Verweise:
[1] Siehe Kapitel 2.7.1.1 der Lernunterlage Einführung in die Empirischen Methoden der Kultur- und Sozialanthropologie
[2] Siehe Kapitel 2.3
Inhalt
2.2 Die Operationalisierung
2.2.1 Die Suche nach Indikatoren
2.2.2 Das Messen
2.2.2.1 Messfehler
2.2.3 Vom Fragebogen zum Codeplan
2.2.3.1 Dateneingabe und Erstellung einer Datenmatrix
2.2.3.2 Umcodierung mit SPSS
2.2.3.3 Automatische Rückcodierung mit SPSS
2.2.1 Die Suche nach Indikatoren
Im Forschungsentwurf werden verschiedene Hypothesen formuliert. Nun benötigt man eine Reihe von Indikatoren, um die Hypothesen[1] beibehalten bzw. verwerfen zu können.
In vielen Fällen ist die Suche nach den Indikatoren einfach. Möchte man z.B. ermitteln, wie warm zur gleichen Jahreszeit verschiedene Orte sind, dann genügt eine Messung mit dem Thermometer. Meist jedoch sind die Forschungsfragen komplexer und nicht mit einer einzigen konkreten Messungsart zu beantworten.
Beispiel 1:
Nehmen wir an, Sie postulieren, dass die Gesellschaft in Nepal sehr ungleich und damit nicht egalitär ist. Nun bräuchten wir eine Reihe von sehr viel spezifischeren Fragestellungen, eigentlich Subhypothesen, deren Synthese zur Beantwortung der allgemeinen Hypothese führen kann. Wir könnten zwischen materieller, rechtlicher und politischer (Un-)Gleichheit unterscheiden. Wir könnten Vermögensverhältnisse in verschiedenen Schichten betrachten; den Zugang zu staatlichen und privaten Ressourcen; wir könnten die Vertretung verschiedener Gruppen der Gesellschaft (Frauen, Adelige, Bauern etc.) im Parlament und anderen öffentlichen Gremien betrachten. Wir könnten die Schulbesuchsquote kontrastiv untersuchen etc.
In all diesen Punkten müssen wir äußerst konkret und präzise werden. Bezüglich des Schulbesuchs könnte man die Zahl der Jahre in der Schule, den maximalen Ausbildungsgrad etc. abfragen. Bezüglich des Vermögens Grundstücke, Häuser, Kapital, Vieh, andere Besitztümer, Leibeigene etc. Wir könnten Einschätzungen abfragen, ob Heiraten zwischen Adeligen und Nichtadeligen als akzeptabel empfunden werden, ob die Befragten annehmen, dass Arme und Reiche vor Gericht die gleichen Chancen haben usw.
Beispiel 2:
Sie nehmen an, dass viele Menschen in Wien AraberInnen ablehnen und oft sogar rassistisch gegenüberstehen. Sie könnten nun in einem Fragebogen an die Wiener Bevölkerung die Wertschätzung des Islams, der arabischen Kultur abfragen. Sie könnten fragen, in welchem Maße man annimmt, dass AraberInnen besonders leicht zu Terrorismus neigen. Sie könnten fragen, ob man sich vorstellen könnte, AraberInnen als angeheiratete Familienmitglieder zu akzeptieren. Sie könnten die Bereitschaft abfragen, AraberInnen Wohnungen zu vermieten. Sie könnten die Befragten ersuchen, die ersten Assoziationen zu nennen, die ihnen beim Begriff AraberInnen einfallen. Sie könnten die Befragten ersuchen, Ihnen das dominante Gefühl zu nennen, welches sie in Gegenwart von AraberInnen spüren usw.
Letztendlich könnte man sich auf einen Schlüssel einigen, mit welchem Anteil die mit den verschiedenen Detailfragen erhaltenen Informationen in einen Sammelparameter (Beispiel 1: Ungleichheit/Gleichheit; Beispiel 2: Rassismus gegenüber AraberInnen) einfließen.
2.2.2 Das Messen
Unter Messung versteht man die quantitative Bestimmung von Sachverhalten in Form einer Messgröße. d.h. wir ordnen diesen Zahlen zu.
Misst man die Temperatur eines Körpers, wird man in unseren Regionen in der Messgröße Celsius messen, in anderen in Fahrenheit etc. Messen wir die Körpergröße, dann messen wir bei größeren Körpern in Metern und Zentimetern, bei Kleinstlebewesen aber auch in Millionstel Metern und darunter. Messen wir das Haushaltseinkommen, werden wir in Euro messen. Bei der Messung von Einstellungen und sozialen Sachverhalten kann man selbst die Messgrößen bestimmen. So könnte man bei der Einschätzung der Sympathie für eine bestimmte Kultur fünf verschiedene Messgrößen festlegen, wie z.B. ’sehr sympathisch’, ’sympathisch’, ’neutral’, ’weniger sympathisch’ und ’unsympathisch’.
Die Antwortkategorien müssen fair und ausgewogen sein
Es wäre tendenziös und unseriös, in der obigen Sympathie-Skala im positiven Bereich nur ’sehr sympathisch’ anzugeben, im negativen jedoch die zwei vorhandenen Unterscheidungen. Dies könnte dazu führen, dass Antwortende, die nur eine leichte Sympathie für die andere Kultur empfinden, zum neutralen Wert ausweichen. Daher gilt als Grundregel, dass die Zahl der möglichen Antwortvarianten bei derartigen Fragen im negativen Bereich genauso hoch wie im positiven Bereich sein soll.
Messungen beinhalten immer das Problem von Messfehlern.
2.2.2.1 Messfehler
Unter Messfehler versteht man die Abweichung des Ergebnisses von Messungen von den realen Gegebenheiten. Wo eine Messung erfolgt, sollte man immer die Möglichkeit von Messfehlern berücksichtigen. Man kann zwischen zufälligen, systematischen und fahrlässigen Messfehlern unterscheiden.
A. Zufällige Messfehler:
Zufällige Messfehler sind von den Messenden nicht zu kontrollieren. Wenn man zum Beispiel eine bestimmte Personengruppe zu einem sensiblen Thema befragen möchte und gerade am Tag vorher ein (den InterviewerInnen unbekanntes) Ereignis eintritt, welches ihre Neigung zu ehrlichen Antworten temporär verändert, während bei Vergleichsgruppen im gleichen Zeitraum nichts Vergleichbares auftritt, können verfälschte Ergebnisse auftreten. Misst man die Regenfälle in der Sahelgegend, kann es sein, dass ein Ort deutlich besser und gleichmäßiger beregnet wird, als die nicht gemessenen Nachbarorte, im nächsten Jahr kann es umgekehrt sein. Es gibt jedoch einen sogenannten Zentralen Grenzwertsatz der Statistik (Wikibooks)[1], nach welchem zufällige Fehler sich im Laufe der Zeit ausgleichen und einer Normalverteilung zustreben. Man kann daher postulieren, dass die zufälligen Messfehler bei häufigen Messungen zum Ausgleich tendieren.
B. Systematische Messfehler:
Systematische Messfehler können durch fehlerhafte Messgeräte entstehen, wie z.B. die Gewichtsmessung durch eine verstellte Waage; die Zeitmessung durch eine ungenaue Uhr; aber auch z.B. eine Kommunikationsform, welche den Zugang zu manchen Informationen kaum erlaubt. So ist es möglich, dass besonders hoch emotionale Angelegenheiten in einer Fremdsprache zu anderen Antworten als in seiner Muttersprache führen. Man überlege sich, ob es einem in einer Fremdsprache ähnlich schwer wie in seiner Muttersprache fällt, z.B. Ich liebe Dich zu sagen, wo beim Aussprechen ähnlicher Sätze auch Assoziationen mit Enttäuschungen u.a. verbunden sein können und damit auch die Angst vor Zurückweisung.
Ein Teil der systematischen Messfehler kann durch stetige Kontrolle und kritische Hinterfragung der Messinstrumente behoben werden.
C. Fahrlässige Messfehler:
Grobe Messfehler beruhen auf menschlichen Fehlern. Man trägt z.B. beim Alter 15 statt 51 ein, schreibt eine Antwort in die falsche Spalte; vergisst eine Frage zu stellen oder zu beantworten. Man vermittelt beim Interview eigene Einstellungen, welche mit großer Wahrscheinlichkeit zu einer veränderten Reaktion des Befragten führen (wenn man z.B. einem Befragten deutlich zeigt, dass man seine Einstellungen und Meinungen geringschätzt).
Weiterführendes zu Messfehlern:
Messfehler (Wikipedia)[2]
Verweise:
[1] https://de.wikibooks.org/wiki/Statistik:_Zentraler_Grenzwertsatz
[2] http://de.wikipedia.org/wiki/Messfehler
2.2.3 Vom Fragebogen zum Codeplan
Unter einem Codeplan verstehen wir die Auflistung aller verwendeten Variablen mit einer eindeutigen Information zur inhaltlichen Bedeutung der numerischen Codes, eventuell noch von weiteren Informationen begleitet, welche sich auf den Messvorgang beziehen.
In einem Codeplan halten wir eindeutig fest, welchen Variablennamen Fragen des Fragebogens entsprechen, wie verschiedene Ausprägungen von Variablen gemessen werden (z.B. in cm für die Körpergröße oder in Ja/Nein für bestimmte Erfahrungen) und wie diese Ausprägungen in eine numerische Form übersetzt werden, was überhaupt erst eine maschinelle quantitative Analyse erlaubt.
Statistikprogramme benötigen automatisch interpretierbare Datentypen
Statistikprogramme benötigen für Berechnungen bestimmte Datentypen, die in der Regel numerisch sind. Kein Statistikprogramm kann in den Antwortkategorien ’sehr’, ’eher schon’, ’durchschnittlich’, ’eher weniger’, ’überhaupt nicht’ eine logische Reihe erkennen, dass also diese Bezeichnungen für verschiedene logische Abstufungen stehen, nämlich für eine Ordinalskala[1].
Damit ein Statistikprogramm wie SPSS die logische Reihenfolge erkennen und danach Analysen über diese bilden kann, müssen die Textwerte in numerische umcodiert werden. Im Codeplan, d.h. der Dokumentation über die ursprünglichen Text- Begriffe und ihrer numerischen Entsprechungen, werden diese Umcodierungen festgehalten. Im obigen Beispiel könnte man ’sehr’ immer durch 1, ’eher schon’ durch 2, ’durchschnittlich’ durch 3, ’eher weniger’ durch 4 und ’überhaupt nicht’ durch 5 ersetzen. Nun ist eine für die Software durchgehende Reihe von 1-5 entstanden, die vom kleinsten zum größten Wert gereiht ist.
Aktuelle Statistikprogramme wie SPSS rechnen intern mit diesen numerischen Daten, können mit einfachen Befehlen jedoch bei der Ausgabe der Ergebnisse automatisch die urspünglichen Textinformationen verwenden.
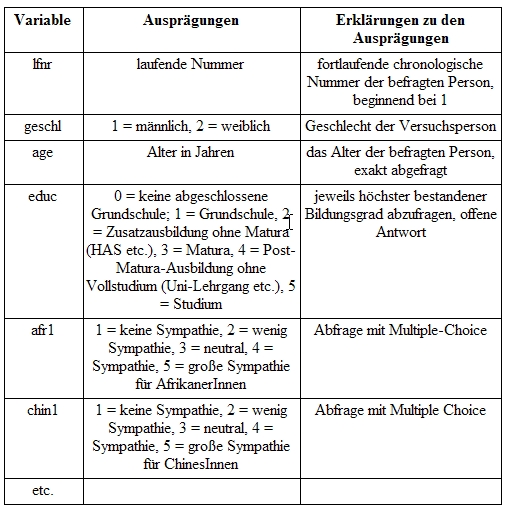
Beispiel eines Codeplans:
Verweise:
[1] Siehe Kapitel 3.1.2.3
2.2.3.1 Dateneingabe und Erstellung einer Datenmatrix
Unter einer Datenmatrix versteht man eine Tabelle, in welcher alle Messungen an den Versuchsobjekten zusammengefasst werden. Die Daten sind normalerweise so angeordnet, dass jede Zeile der Datenmatrix alle Messungen an einem einzelnen Datenobjekt enthält. In den Zeilen stehen somit von links nach rechts die Angaben zu einer Person (bzw. zu den Untersuchungsobjekten), während in den Spalten die Variablen eingetragen werden.
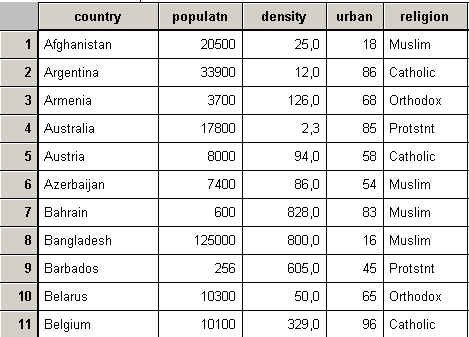
Siehe z.B. die ersten Spalten und Zeilen der SPSS-Datei zur weltweiten Entwicklung world95.sav:
Die Untersuchungsobjekte sind hier eindeutig durch ihre in der ersten Spalte stehenden (Länder-)Namen identifiziert. Von links nach rechts werden danach in den einzelnen Zeilen durch Variable Informationen zu den jeweiligen Ländern angegeben: Bevölkerungsgröße, Bevölkerungsdichte, Prozentsatz der städtischen Bevölkerung, Religion etc.
Es ist äußerst empfehlenswert, die Datenmatrix in der hier beschriebenen Weise zu verwalten, da alle führenden und gängigen Analyse- und Darstellungsprogramme (Excel, SPSS etc.) die gleiche Anordnung verwenden.
2.2.3.2 Umcodierung mit SPSS
SPSS benötigt gleichzeitig für viele Funktionen numerische Daten, wo Daten in String (oder Text-)Format vorliegen. So kann SPSS bei reinen Textdaten, wie z.B. ’Sehr Gut’ oder ’Gut’ nicht erkennen, dass ’Sehr Gut’ eine höhere Intensität bzw. Qualität als ’Gut’ wiederspiegelt. SPSS würde eine sinnvolle Rangfolge jedoch in numerischer Form erkennen.
SPSS erlaubt es, Stringvariable automatisch in numerische zu codieren.
Dazu benützen Sie die Funktion TRANSFORMIEREN - UMCODIEREN in der Menüleiste. Nun können Sie sich entscheiden, ob die Umcodierung in die gleiche oder in eine andere Variable erfolgen soll. Es ist besser, sich für eine andere Variable zu entscheiden, da durch die Umcodierung (man kann auch mehrere Werte zu einem einzigen neuen umcodieren) Informationsverlust auftreten kann (ob willentlich oder durch einen Bedienungsfehler). Dieses Problem wird durch Umcodierung in eine neue Variable ausgeschlossen.
Sie wählen nun die Variable aus, welche umcodiert werden soll und geben im Feld Ausgabevariable einen neuen Namen dafür ein (der aus Gründen verschiedenster Kompatibilität) acht Zeichen nicht überschreiten darf. Im Feld darunter können Sie jedoch einen beliebig langen und expressiveren Namen wählen.
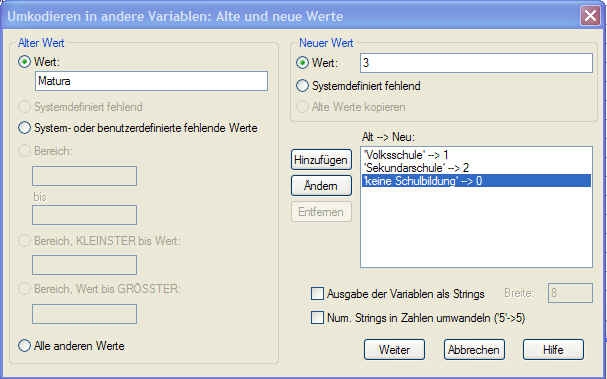
Klicken Sie nun auf Alte und neue Werte. Wenn Sie einzelne Werte umcodieren möchten, geben Sie im Feld Wert denselben ein (z.B. Matura). Nun benötigen Sie einen neuen Wert dafür. Dafür könnten Sie z.B. die Zahl 3 im Feld Neuer Wert eingeben. Im oben angeführten Beispiel wären verschiedene abgeschlossene Ausbildungsstufen in eine logische Reihenfolge gebracht.
Falls Sie mehrere (numerische) Werte zu einem einzigen neuen zusammenfassen möchten, können Sie einen Bereich angeben (z.B. Bereich 20 bis 29), wenn Sie alle zwischen 20-29jährigen in eine einzige Altersklasse ’zwischen 20 und 30' einbringen möchten). Klicken Sie nach jeder einzelnen Angabe zur Umcodierung auf Hinzufügen.
Klicken Sie am Ende auf Weiter und dann auf OK. Ihre Daten werden nun in die neue Variable umcodiert. Erst jetzt wäre es Ihnen möglich, dass SPSS die Ausbildung nach Jahren und Qualität sinnvoll reihen kann und natürlich auch viele weitere (damit zusammenhängenden) Analysen rechnen kann. So wäre erst jetzt die Berechnung einer Korrelation[1] zwischen dem Ausbildungsgrad und dem Einkommen möglich.
Verweise:
[1] Siehe Kapitel 3.5.3
2.2.3.3 Automatische Rückcodierung mit SPSS
Damit SPSS mit Daten rechnen kann, wurden diese in numerischer Form eingegeben oder in eine neue numerische Variable umcodiert. Wenn Sie nun eine auf diesen neuen Variablen basierende Analyse starten, wirken die Ergebnisse ohne zusätzliche Information wenig informativ.
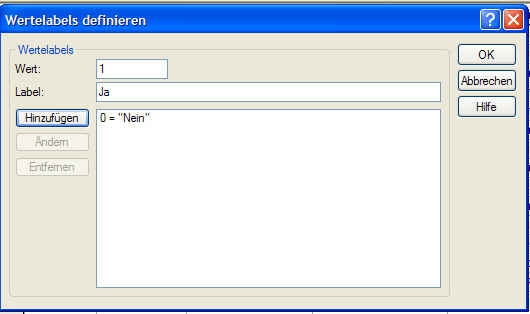
Niemand könnte ohne Zusatzinformation wissen, dass 0 für Nein und 1 für Ja steht. Damit SPSS intern mit den numerischen Daten rechnen kann, wir jedoch bei allen Ausgaben (Diagramme, Analysen etc.) informative Bezeichnungen erhalten, klicken wir in SPSS unten links auf die Variablenansicht. Im neuen Fenster finden wir in der Zeile der neuen Variable den Punkt Variablenlabel. Nach Doppelklick darauf erscheint folgendes Fenster:
Wir geben nun für den Wert das gewünschte Label ein. Wir möchten, dass statt 0 der aussagekräftige Text Nein erscheint, statt 1 der aussagekräftige Wert Ja. Nach Eingabe aller automatisch durchzuführenden Änderungen klicken wir auf OK.
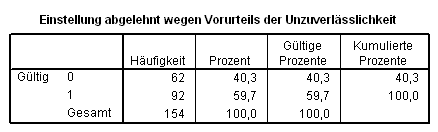
Wenn wir nun die gleiche Häufigkeitsberechnung wie oben durchführen, erhalten wir nun folgende leichter verständliche Tabelle:
Nächstes Kapitel: 2.3 Gütekriterien quantitativer Untersuchungen