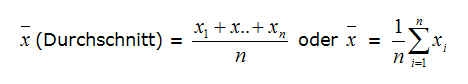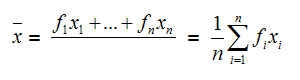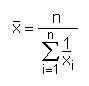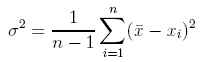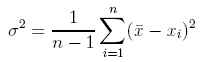Grundlagen Statistischer Auswertungsverfahren
Contents
- 1 Grundlagen statistischer Auswertungsverfahren
- 2 1. Funktion und Sinn von Statistik
- 3 1.1 Qualitative und Quantitative Forschungsmethoden - Gegensatz oder Ergänzung?
- 4 1.2 Formen der Statistik
- 5 1.3 Wahrscheinlichkeiten, nicht Gewissheit
- 6 2. Von der Fragestellung zur statistischen Analyse
- 7 2.1 Die Grundpopulation: worüber wir Aussagen machen
- 7.1 Elemente, Variable und Ausprägungen
- 7.2 Befragung der gesamten Grundpopulation nur selten möglich
- 7.3 Öffentliche Quellen für Daten über Grundpopulationen
- 7.4 2.1.1 Die Stichprobe (Sample)
- 7.5 2.1.2 Teil- oder Vollerhebung?
- 7.6 2.1.3 Die Ziehung (Auswahl) der Stichprobe
- 7.6.1 2.1.3.1 Geschichtete Stichprobenauswahl (Quotenstichprobe)
- 7.6.2 2.1.3.1.1 Proportional geschichtete Stichproben
- 7.6.3 2.1.3.1.2 Disproportional geschichtete Stichproben
- 7.6.4 2.1.3.1.3 Laufende Kontrolle der Schichtung
- 7.6.5 Während der Befragungsphase laufende Kontrolle der Schichtung erforderlich
- 7.6.6 Berechnung
- 7.6.7 2.1.3.2 Zufallsstichproben
- 7.6.8 2.1.3.2.1 Einfache Zufallsstichprobe
- 7.6.9 2.1.3.2.2 Systematische Zufallsstichprobe
- 7.6.10 2.1.3.2.3 Geschichtete Zufallsstichprobe
- 7.6.11 2.1.3.3 Willkürliches Auswahlverfahren
- 7.6.12 2.1.3.4 Klumpenstichproben
- 7.7 2.1.4 Repräsentativität
- 7.8 2.1.5 Was tun, wenn die Grundpopulation nicht bekannt ist?
- 8 2.2 Die Operationalisierung
- 9 2.3 Gütekriterien quantitativer Untersuchungen
- 10 2.4 Fehlerquellen bei statistischer Arbeit
- 10.1 2.4.1 Fehler erster und zweiter Art
- 10.1.1 Hypothesen am Beginn der Untersuchung
- 10.1.2 Annahme oder Verwerfung von Hypothesen ist immer an Wahrscheinlichkeiten gebunden
- 10.1.3 Fehlerhafte Verwerfung bzw. Annahme von Hypothesen möglich
- 10.1.4 Mit der Zahl der statistischen Berechnungen steigt die Wahrscheinlichkeit von Fehlern der 1. oder 2. Art
- 10.1.5 Kontrolle durch qualitative Überlegungen erforderlich
- 10.2 2.4.2 Fehlerhafte oder mangelnde Daten
- 10.1 2.4.1 Fehler erster und zweiter Art
- 11 3. Ausgewählte statistische Grundlagen und Analysemethoden
- 12 3.1 Notwendiges Wissen für die Wahl geeigneter statistischer Analysemethoden
- 12.1 Analysemethoden sind abhängig von Datenart, -ausprägung, -anzahl und -verteilung:
- 12.2 Körpergrößen und Lieblingsobst
- 12.3 3.1.1 Arten von Messwerten (Daten)
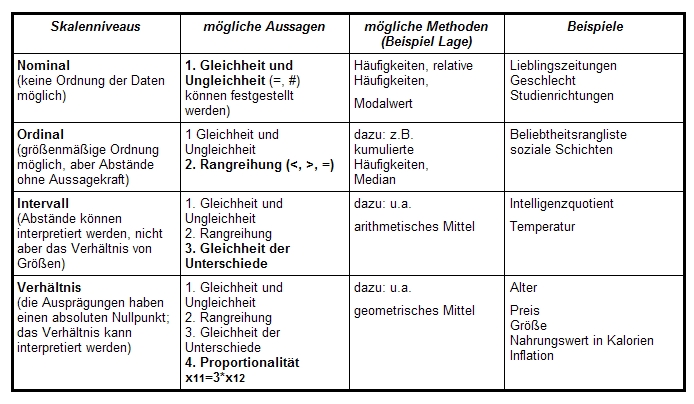
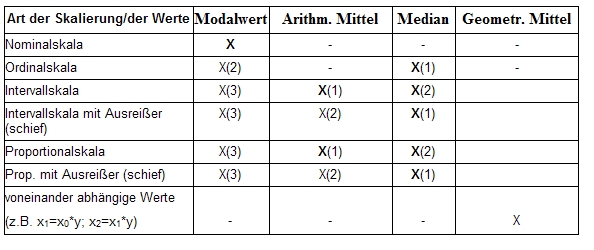
- 12.4 3.1.2 Skalenniveaus
- 12.5 3.1.3 Verteilungen
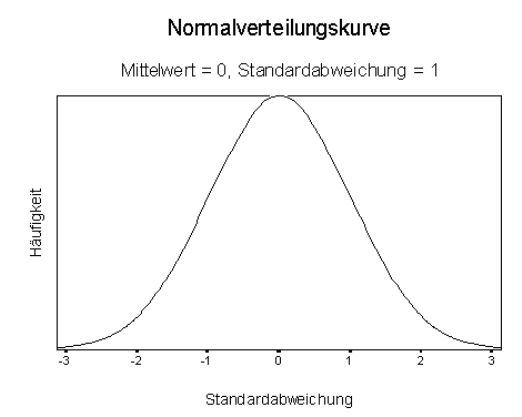
- 12.5.1 3.1.3.1 Normalverteilung
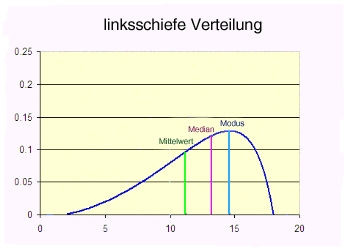
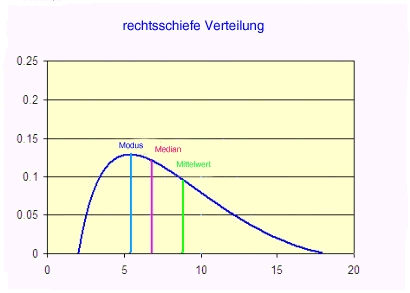
- 12.5.2 3.1.3.2 Andere Verteilungsformen
- 12.5.3 3.1.3.3 Test auf Normalverteilung
- 12.5.4 Erkennung mit SPSS
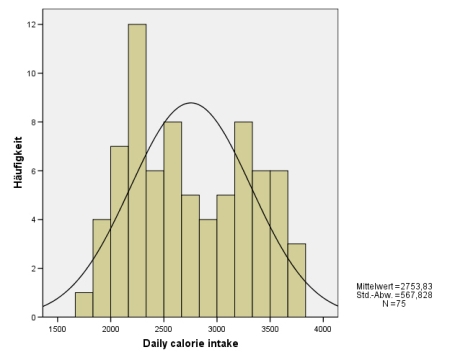
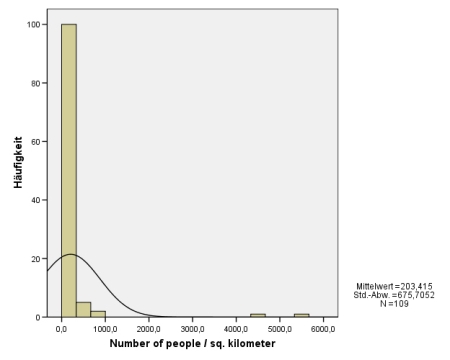
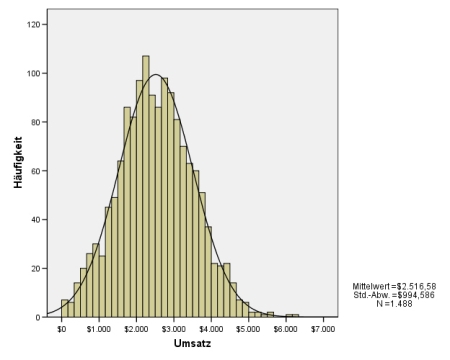
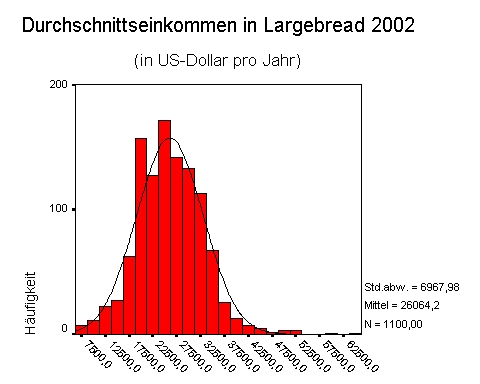
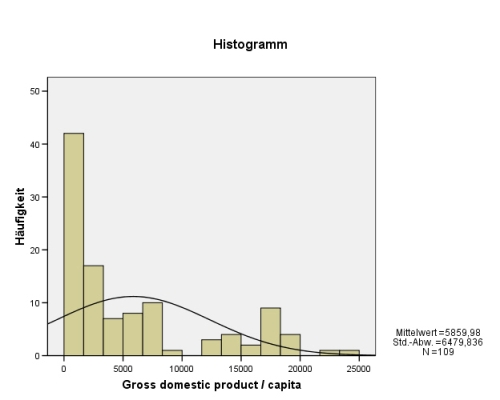
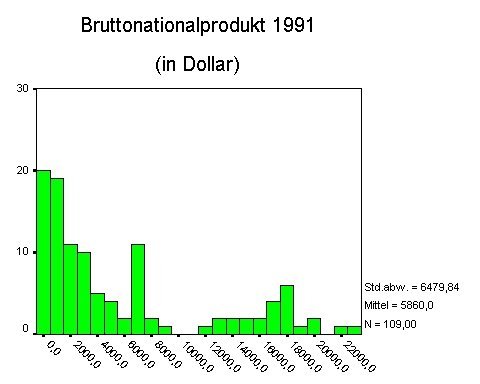
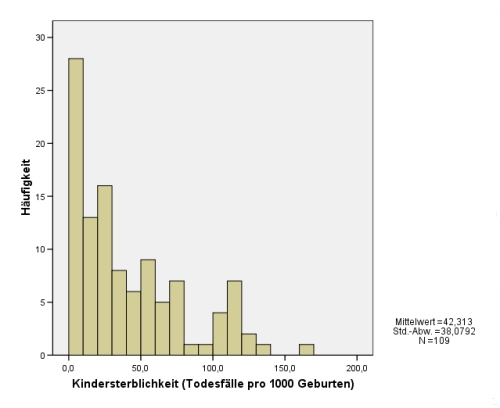
- 12.5.5 3.1.3.3.1 Optischer Nachweis einer Normalverteilung: das Histogramm
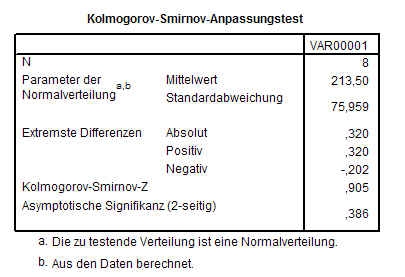
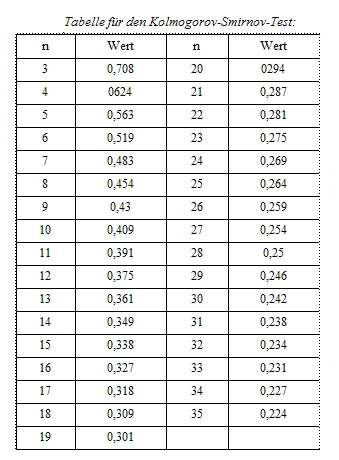
- 12.5.6 3.1.3.3.2 Nachweis der Normalverteilung: Kolmogorov-Smirnov-Test
- 12.5.7 3.1.3.3.2.1 Kolmogorov-Smirnov-Test mit SPSS
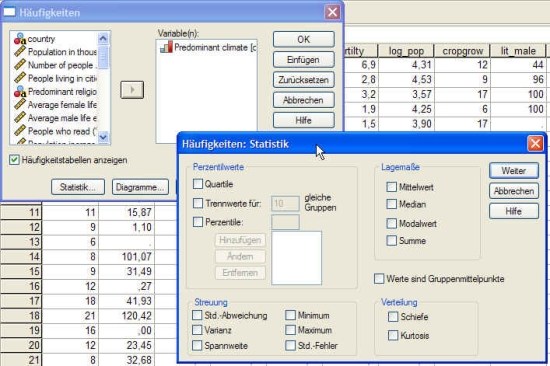
- 13 3.2 Die Ermittlung von Häufigkeiten
- 14 3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz
- 15 3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’
- 15.1 Grafische Darstellung der Streuung durch Histogramme
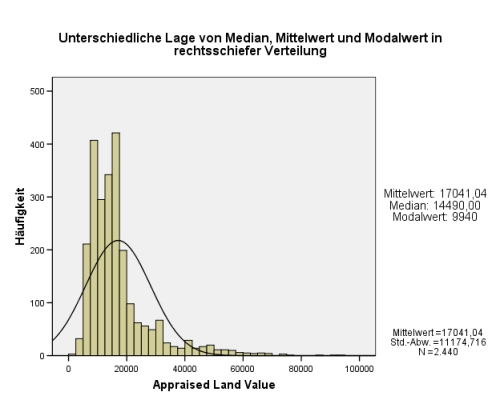
- 15.2 Lagemaße zeigen oft nur verzerrtes Bild der Realität bzw. Normalität
- 15.3 3.4.1 Varianz
- 15.4 3.4.2 Standardabweichung
- 15.5 3.4.3 Perzentile
- 15.6 3.4.4 Berechnung von Streuungsmaßen mit SPSS
- 15.7 3.4.5 Vergleichende grafische Darstellung von Streuung und Lage mit Box-Plots
- 16 3.5 Der Zusammenhang zwischen Variablen
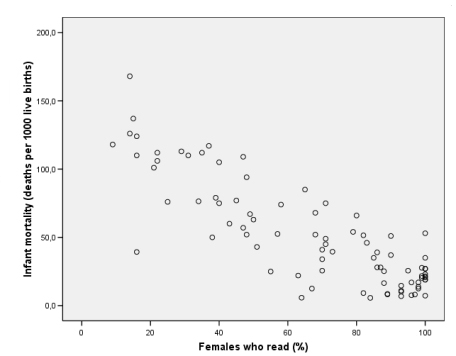
- 16.1 3.5.1 Optische Erkennung von Zusammenhängen
- 16.2 3.5.2 Kreuztabellen-Analyse
- 16.3 3.5.3 Die Korrelation
- 16.3.1 Vorsicht bei vorschneller Herstellung von Zusammenhängen
- 16.3.2 3.5.3.1 Maßkorrelation
- 16.3.3 3.5.3.1.1 Berechnung der Maßkorrelation mit SPSS
- 16.3.4 3.5.3.2 Rangkorrelation R (Krueger-Spearman)
- 16.3.5 3.5.3.2.1 Berechnung der Rangkorrelation mit SPSS
- 16.3.6 3.5.3.3 Rangkorrelation Tau (Kendall)
- 16.3.7 3.5.3.3.1 Berechnung von TAU mit SPSS
- 16.3.8 3.5.3.4 Aussagekraft einer Korrelation
- 16.3.9 3.5.3.4.1 Wann sind Korrelationen bemerkenswert?
- 16.3.10 3.5.3.4.2 Verdeckte Korrelation
- 16.3.11 3.5.3.4.3 Scheinkorrelationen und Störvariable
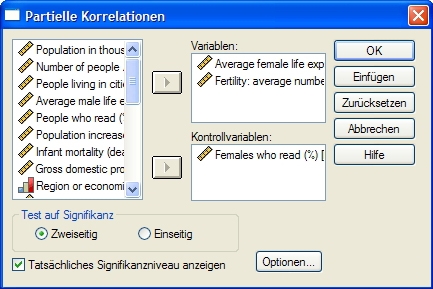
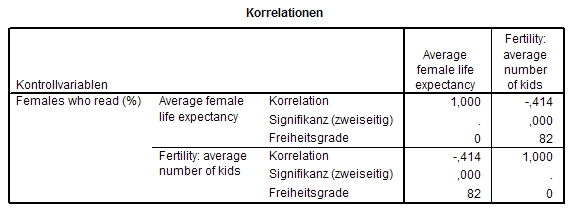
- 16.3.12 3.5.3.4.3.1 Partielle Korrelation mit SPSS
- 16.3.13 3.5.3.4.4 Signifikanz der Korrelation
- 16.3.14 3.5.3.4.4.1 Signifikanz mit SPSS
- 16.3.15 3.5.3.5 Kovarianz
- 16.4 3.5.4 Regression
- 17 3.6 Die grafische Darstellung statistischer Ergebnisse
- 17.1 Ein Bild sagt mehr als 1000 Worte
- 17.2 Vorteil von Diagrammen liegt in Einfachheit der Darstellung
- 17.3 Nicht jedes Diagramm ist für jede Datenlage geeignet.
- 17.4 Begleitinformationen sind wichtig
- 17.5 Was in Diagrammen, was im Text?
- 17.6 3.6.1 Arten von Diagrammen
- 17.6.1 Viele Programme ermöglichen die Erstellung von Diagrammen
- 17.6.2 3.6.1.1 Kreisdiagramme
- 17.6.3 Besonders gut geeignet für die Darstellung relativer Anteile sind Torten- oder Kreisdiagramme:
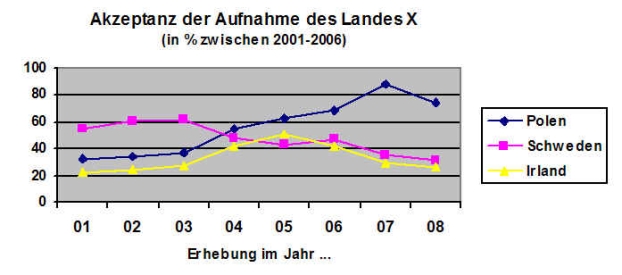
- 17.6.4 3.6.1.2 Liniendiagramme
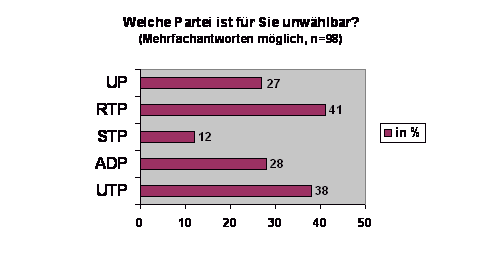
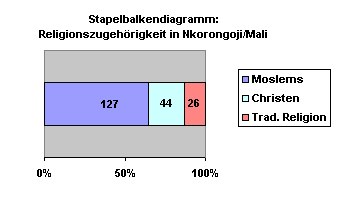
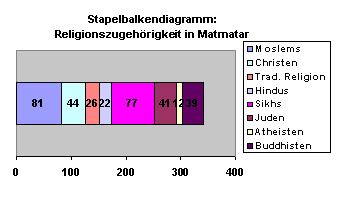
- 17.6.5 3.6.1.3 Balkendiagramme
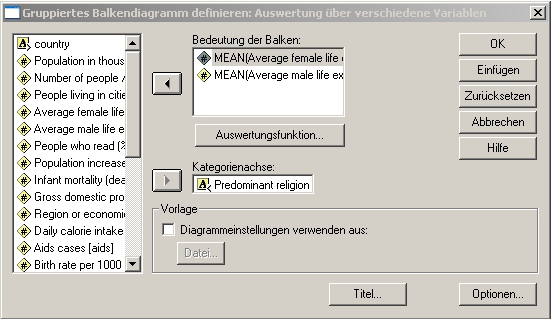
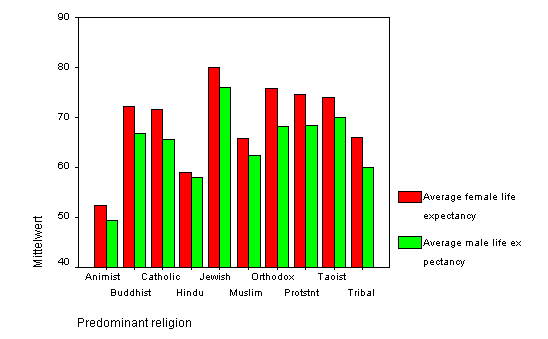
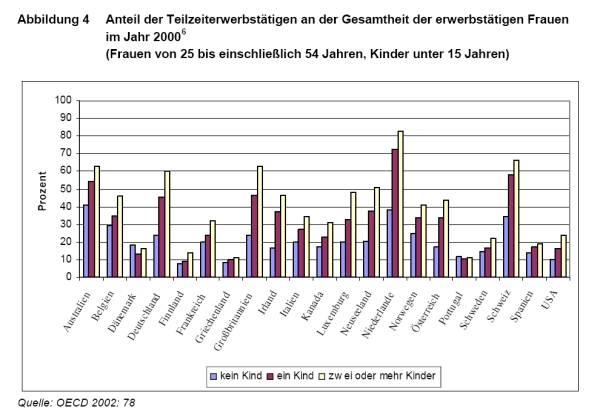
- 17.6.6 3.6.1.3.1 Gruppierte Balkendiagramme mit SPSS
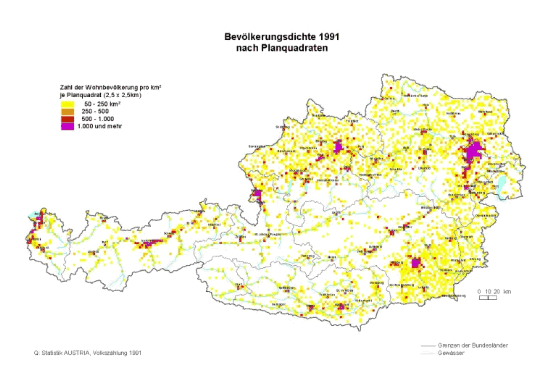
- 17.6.7 3.6.1.4 Kartogramme
- 17.6.8 Kartogramme in Wahlanalysen häufig
- 17.6.9 3.6.1.5 Histogramme
- 17.6.10 3.6.1.6 Streudiagramme
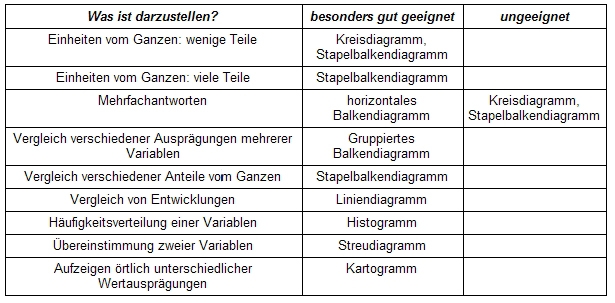
- 17.7 3.6.2 Welches Diagramm für welche Daten?
- 17.8 3.6.3 Notwendige Begleitinformationen von Diagrammen
- 18 4. Software für quantitative Forschungsprojekte
- 19 4.1 Was kann Excel?
- 20 4.2 Was kann MS Access?
- 21 4.3 Profi-Programme: SPSS und Statistica
- 22 4.4 Datentransfer zwischen Programmen: Von Excel und Access zu SPSS
- 23 4.5 Umcodierung
- 24 5. Lexikon statistischer Grundbegriffe
- 25 5.1 A-C
- 25.1 Abhängige Variable
- 25.2 Alpha-Fehler
- 25.3 Alternativhypothese
- 25.4 Analytische Statistik (auch Schließende Statistik oder Inferenzstatistik)
- 25.5 Arithmetisches Mittel (oder Durchschnitt/-swert)
- 25.6 Balkendiagramm (auch Säulen- oder Blockdiagramm)
- 25.7 Bestimmtheitsmaß (auch Determinationskoeffizient)
- 26 5.2 D-F
- 27 5.3 G-I
- 28 5.4 J-M
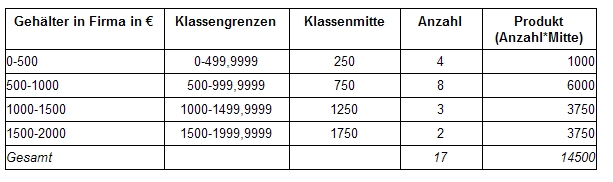
- 28.1 Klasse
- 28.2 Klassifizerung (auch Klassierung).
- 28.3 Konfidenzinterall (auch Vertrauensintervall)
- 28.4 Kreisdiagramm (oder Tortendiagramm)
- 28.5 Kreuztabelle (auch Kontingenztabelle, -tafel)
- 28.6 Kumulative Häufigkeit (auch kumulierte H.)
- 28.7 Lagemaße (auch Zentralwerte oder Maße der zentralen Tendenz)
- 28.8 Liniendiagramm (auch Kurvendiagramm)
- 28.9 Median (auch Zentralwert)
- 28.10 Merkmal (auch Variable)
- 28.11 Messniveau (auch Skalenniveau)
- 28.12 Mittelwert (auch Arithmetisches Mittel)
- 28.13 Modalwert (auch Modus)
- 28.14 Modus (siehe Modalwert)
- 28.15 Multivariate Verfahren (oder m. Analyse)
- 29 5.5 N-P
- 29.1 Nichtparametrische Verfahren (auch parameterfreie Verfahren)
- 29.2 Normalverteilung (auch Gaußverteilung)
- 29.3 p-Wert (auch Überschreitungswahrscheinlichkeit)
- 29.4 Partielle Korrelation (auch Partialkorrelation)
- 29.5 Proportionalskala (auch Verhältnisskala)
- 29.6 Produkt-Moment-Korrelation (auch Pearson’scher Korrelationskoeffizient)
- 30 5.6 Q-R
- 31 5.7 S-T
- 31.1 Säulendiagramm
- 31.2 Schichtung
- 31.3 Schließende Statistik
- 31.4 Selektion
- 31.5 Signifikanz
- 31.6 Signifianzniveau
- 31.7 Skala
- 31.8 Skalenniveau
- 31.9 Spannweite
- 31.10 Spearman’s Rho (oder Spearmans Korrelationskoeffizient)
- 31.11 Störvariable (oder Störgrößen)
- 31.12 Streudiagramm (auch Scatterplot)
- 31.13 Streuungsmaße (auch Dispersionsmaße)
- 31.14 Tau (auch Kendall’s Tau)
- 32 5.8 U-Z
- 33 6. Literatur, Ressourcen und Links
- 34 6.1 Quantitative Forschungsmethoden
- 35 6.2 Fragebogen-Abfrage
- 36 6.3 Methoden
- 37 6.4 Repräsentativität
- 38 6.5 Statistik-Software
- 39 6.6 Terminologie
- 40 6.7 Statistik-Quellen
Grundlagen statistischer Auswertungsverfahren
Quelle: http://www.univie.ac.at/ksa/elearning/cp/quantitative/quantitative-titel.html
Erwin Ebermann
Institut für Kultur- und Sozialanthropologie
Kapitelübersicht
1. Funktion und Sinn von Statistik
- 1.1 Qualitative und Quantitative Forschungsmethoden - Gegensatz oder Ergänzung?
- 1.2 Formen der Statistik
2. Von der Fragestellung zur statistischen Analyse
- 2.1 Die Grundpopulation: worüber wir Aussagen machen
- 2.1.1 Die Stichprobe (Sample)
- 2.1.2 Teil- oder Vollerhebung?
- 2.1.3 Die Ziehung (Auswahl) der Stichprobe
- 2.1.4 Repräsentativität
- 2.1.5 Was tun, wenn die Grundpopulation nicht bekannt ist?
- 2.1.1 Die Stichprobe (Sample)
- 2.2 Die Operationalisierung
- 2.3 Gütekriterien quantitativer Untersuchungen
- 2.4 Fehlerquellen bei statistischer Arbeit
3. Ausgewählte statistische Grundlagen und Analysemethoden
- 3.1 Notwendiges Wissen für die Wahl geeigneter statistischer Analysemethoden
- 3.2 Die Ermittlung von Häufigkeiten
- 3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz
- 3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’
- 3.5 Der Zusammenhang zwischen Variablen
- 3.6 Die grafische Darstellung statistischer Ergebnisse
4. Software für quantitative Forschungsprojekte
- 4.1 Was kann Excel?
- 4.2 Was kann MS Access?
- 4.3 Profi-Programme: SPSS und Statistica
- 4.4 Datentransfer zwischen Programmen: Von Excel und Access zu SPSS
- 4.5 Umcodierung
\[(.*)\] Siehe Kapitel
1. Funktion und Sinn von Statistik
Weitverbreitete Scheu vor statistischen Methoden
Was bringt Statistik, was bringen quantitative Forschungsmethoden? Viele Menschen stehen ihnen skeptisch gegenüber und dies teilweise leider zurecht. Allzuleicht kann mit Statistiken Unfug getrieben werden und nicht immer sind die BetrachterInnen statistisch aufbereiteter Daten genügend geschult, um bewusste Verzerrungen zu erkennen. Richtig verwendet jedoch, ist die Statistik ein unverzichtbares Hilfsmittel, um - losgelöst von der subjektiven Wahrnehmung - die Systematik von Tendenzen und Zusammenhängen in verschiedensten Lebensbereichen aufzeigen zu können.
Statistik in der Alltagserfahrung
Ob wir wollen oder nicht, auch wenn wir niemals etwas von Statistik gehört haben, so wenden wir dennoch meist unreflektiert und unsystematisch Methoden an, welche statistischen Verfahren ähneln. D.h. wir versuchen, von einem begrenzten Erfahrungsschatz auf allgemeine Sachverhalte zu schließen. Jede Erfahrung, die wir machen, beeinflusst mit einer gewissen Wahrscheinlichkeit unsere zukünftigen Handlungs- und Denkweisen. Wir vermeiden vielleicht den Kontakt mit bestimmten Gruppen der Gesellschaft, weil sie uns wenig kooperativ erscheinen; wir fällen aufgrund einzelner Geschehnisse verallgemeinernde Urteile über Bekannte, dass sie diese oder jene Eigenschaft aufweisen, über Menschen, welche in der Öffentlichkeit stehen, über den öffentlichen Verkehr:
Ilse ist äußerst hilfsbereit!
Mit Georg kann man darüber nicht sprechen!
Die 5er-Linie kommt immer verspätet!
Immer wenn das Wochenende kommt, regnet es!
Alle diese Aussagen basieren auf dem in der Statistik gängigen Vorgang, von einer begrenzten Erfahrung bzw. von einem begrenzten Datenschatz auf alle möglichen Erfahrungen bzw. Daten hochzurechnen, wobei wir bei diesen Aussagen jedoch wichtige Grundprinzipien der Statistik nicht berücksichtigen. Diese ’unbewussten’ Anwendungen statistischer Prinzipien ähneln den Versuchen von Couchpotatoes, die Fussballkünste eines Ronaldinho in der Praxis nachzuvollziehen.
Häufige Fehler bei der ’unbewussten’ Verwendung statistischer Methoden
Wir möchten mit diesen Aussagen ausdrücken, dass bestimmte Grundtendenzen vorkommen, dass diese systematisch sind. Aber sind sie das? Haben wir die Rahmbendingungen genügend beachtet? Ist Georg vielleicht nur mir gegenüber nicht gesprächsbereit? Gilt Ilse vielleicht allen anderen gegenüber als schroff und unkooperativ? Kommt die 5er-Linie nur zu bestimmten Tageszeiten, an welchen gerade ich sie immer benutze, zu spät und zu anderen Zeitpunkten pünktlich? Nehme ich schlechtes Wetter unter der Woche gar nicht wahr, weil ich mich im Büro befinde? Stimmt mein eigener Eindruck oder beharre ich auf meinem allerersten und möchte neue Erfahrungen nicht wahrnehmen?
Statistik muss mit Sorgfalt eingesetzt werden
Die Statistik gibt uns Methoden in die Hand, Vorurteile kritischer zu beleuchten und die Wahrscheinlichkeit[1] scheinbaren Wissens zu beurteilen, falls sie mit Verantwortungsbewusstsein und Sorgfalt verwendet werden. Sie ist besonders dann von großer Bedeutung, wenn wir - losgelöst von singulären Ereignissen oder Elementen - allgemeine Aussagen machen möchten. Sie ist dementsprechend kein Gegensatz zu qualitativen Forschungsmethoden, sondern eine unverzichtbare Ergänzung[2] zu diesen.
Verweise:
[1] Siehe Kapitel 1.3
[2] &&& http://www.univie.ac.at/ksa/elearning/cp/qualitative/qualitative-50.html
1.1 Qualitative und Quantitative Forschungsmethoden - Gegensatz oder Ergänzung?
Quantitative und qualitative Forschungsmethoden haben unterschiedliche Potentiale und Möglichkeiten und sind dementsprechend kein Gegensatz, sondern ergänzen sich gegenseitig.
Häufig Misstrauen gegenüber Statistik in Geistes- und Kulturwissenschaften
In den Wissenschaften vom Menschen, wie z.B. der Sozial- und Kulturanthropologie, sind qualitative Forschungsmethoden[1] meist deutlich populärer als quantitative. Es mutet zu nüchtern an, zu festschreibend, zu klischeehaft, Menschen durch eine Reihe von meist kurzen Indikatoren beschreiben[2] zu wollen. GestaltpsychologInnen würden formulieren: "Das Ganze ist mehr als die Summe seiner Einzelteile."
Zur Tiefe benötigt man qualitative Ansätze
Und sie haben in Vielem zweifellos recht. Wir benötigen in der Regel qualitative Methoden, um feingewobene Motivforschung zu betreiben, um versteckte Aspirationen, Einstellungen, Eigenheiten zum Vorschein zu bringen. Wie könnte ein kurzer Fragebogen von einer halben Stunde Dauer das gleiche Wissen über die gleiche Person zum Vorschein bringen wie eine Befragung über mehrere Tage, die noch dazu weitgehend dem Rythmus des/der Befragten folgt? Das geht nicht. Und ginge es nur um die Befragung und Eigenheiten einzelner Individuen, etwa um eine Biographie, benötigen wir die Quantitativen Forschungsmethoden eigentlich gar nicht.
Von der Tiefe zur Breite
Nehmen wir nun aber an, jemand hätte mit großer Sensiblität und Mühe aus zehn Personen sehr viel zum Vorschein gebracht, an Ängsten, Erwarungshaltungen, biographischen Daten, an Erfahrungen, Einstellungen usw. Nehmen wir an, alle zehn Befragten wären AfrikanerInnen gewesen. Könnten wir ihm/ihr nun die Frage stellen, uns zu sagen, wo AfrikanerInnen Elemente des Lebens anders wahrnehmen, anders reagieren, anders geprägt sind? Er/Sie könnte mit einem rein qualitativen Ansatz darauf keine Antwort geben. Er/Sie könnte nur antworten: "Die meisten der befragten zehn Personen sind wegen der Suche nach Arbeit nach Österreich gekommen. Die Hälfte von ihnen empfindet ein größeres Maß von Einsamkeit etc." Jede Aussage über Tendenzen der größeren Gruppe, zu der die Befragten gehören, wäre vermessen. Wie soll man wissen, ob die zehn Befragten nicht vielleicht die einzigen in der afrikanischen Community sind, die bestimmte Eigenschaften aufweisen, vielleicht auch die einzigen, welche überhaupt bereit sind, mit den weißen ForscherInnen darüber zu sprechen?
Qualitative und quantitative Methoden ergänzen und erfordern einander
An dieser Stelle werden quantitative Forschungsmethoden als Ergänzung[3] zu den qualitativen unverzichtbar. Beim quantitativen Untersuchungsansatz würde man mit geeigneten Methoden versuchen, die Befragten[4] bereits so auszuwählen, dass sie in den wesentlichen Bereichen ein realistisches Abbild der hier lebenden afrikanischen Community bilden.
Tiefe durch qualitative, Breite durch quantitative Methoden
Quantitative Forschungsmethoden folgen oft qualitativen. Qualitative Untersuchungen liefern hochinteressante Informationen über Menschen, die zu einer bestimmten Berufsgruppe, Region oder Kultur gehören. In von Oralliteratur geprägten Regionen werden z.B. viele Bereiche einer häufigeren Neuinterpretation unterliegen, da mit der schriftlichen Fixierung oft auch eine erhöhte Stabilisierung eines Sachverhalts einhergeht. Zu Randbereichen mag es daher eine Fülle von Interpretationen geben. So mag ein Informant Gedanken äußern, welche erstaunliche Ähnlichkeit mit Reinkarnationsphilosophien anderer Weltgegenden aufweisen. Nun wird es - falls es ums Weltbild der betreffenden Kultur geht - wichtig sein, zu klären, ob nur diese Person oder die ganze Gesellschaft an das Phänomen der Reinkarnation glaubt. Nun könnte man mit einer kleinen quantitativen Erhebung, bei der die verschiedenen Gruppen der Gesellschaft befragt werden, schnell herausfinden, ob für diese Vorstellung die Biographie des Individuums (wie z.B. auf Reisen durch Kontakt mit anderen Völkern erworben), die Prägung einer Kaste innerhalb des Volkes oder die Prägung der ganzen Bevölkerung verantwortlich ist. Und dann könnte man eine allgemeinere Aussage über diesen Sachverhalt machen: "In diesem Volk glauben nur die Älteren an die Reinkarnation, die Jüngeren haben vorwiegend das christliche oder islamische Modell übernommen etc.".
Verweise:
[1] &&& http://www.univie.ac.at/ksa/elearning/cp/qualitative/qualitative-titel.html
[2] &&& http://www.univie.ac.at/ksa/elearning/cp/schreiben/schreiben-2.html
[3] &&& http://www.univie.ac.at/ksa/elearning/cp/qualitative/qualitative-50.html
[4] Siehe Kapitel 2.1
1.2 Formen der Statistik
Man unterscheidet im wesentlichen zwei verschiedene Formen der Statistik:
- die deskriptive Statistik, bei der mit einfachen Maßzahlen und Grafiken Wesentliches über einen Untersuchungsgegenstand ausgedrückt werden soll, sowie
- die schließende oder analystische Statistik, die sich im wesentlichen die Frage stellt, inwieweit das Gemessene als Abbild der Realität geeignet ist.
Vergleich anhand der Einkommenssituation in Bangladesh
Nehmen wir an, wir untersuchen die Einkommensituation in zwei benachbarten Dörfern in Bangladesh. Wir stellen in den beiden Dörfern ein bestimmtes Durchschnittseinkommen fest und drücken dies in einer Maßzahl aus, z.B. dem Median[1] oder dem Mittelwert[2]. Mittels eines Balkendiagramms[3] zeigen wir auch optisch, dass das Durchschnitseinkommen von Dorf A höher ist als das von Dorf B. Bisher sind wir immer noch im Bereich der deskriptiven Statistik geblieben.
Wenn wir uns nun allerdings die Frage stellen, ob der von uns festgestellte Einkommensunterschied zwischen den beiden Dörfern zufälliger Natur oder hoch signifikant[4] ist, dann geraten wir mit den entsprechenden Methoden (z.B. dem T-Test (Wikipedia)[5]) in den Bereich der schließenden Statistik.
Verweise:
[1] Siehe Kapitel 3.3.3
[2] Siehe Kapitel 3.3.2
[3] Siehe Kapitel 3.6.1.3
[4] Siehe Kapitel 1.3.2
[5] http://de.wikipedia.org/wiki/T-Test
1.2.1 Deskriptive Statistik
Die deskriptive Statistik hat zum Ziel, die wesentlichen Eigenheiten eines Untersuchungsgegenstandes zusammenzufassen und in wenigen Maßzahlen bzw. Diagrammen klar und verständlich zu beschreiben.
Die Aussagen der deskriptiven Statistik beziehen sich dabei immer nur auf die untersuchte Stichprobe. Die Darstellungsformen liegen in Maßzahlen, in Grafiken[1] und Tabellen. Häufige Maßzahlen der deskriptiven Statistik sind z.B. Mittelwerte[2] oder die Streuung einer Stichprobe[3] oder deren grafische Entsprechungen in Form z.B. von Kreis- oder Stabdiagrammen[4].
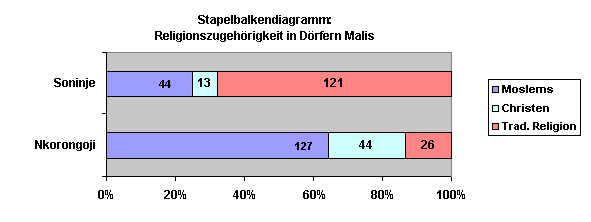
Beispiel: Vergleichende Dorfstudien in Mali
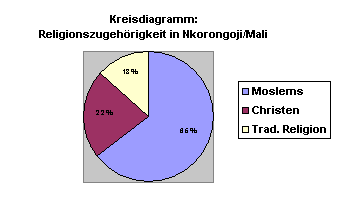
Wir untersuchen zwei Siedlungen in Mali in Westafrika. Wir befragen jeweils 50 Personen aus den beiden Siedlungen zu Einschätzungen eines in der Gegend lebenden Volkes. Wir halten nüchtern fest, wie diese Einschätzungen ausfallen. Wir können dann z.B. angeben, dass das rinderzüchtende Volk der Fulbe in Nkorongoji relativ negativ betrachtet wird, in der Stadt Kita hingegen eher positiv. Das sind nüchterne Beschreibungen = Deskriptionen.
Bei der deskriptiven Statistik untersuchen wir nicht, ob diese Unterschiede der Einschätzungen der Fulbe möglicherweise zufälliger Natur sein könnten (weil die Stichproben[5] zu klein waren; die Einschätzungsabstände zu klein; weil wir durch viel Pech trotz sorgfältiger Auswahl der Befragten im Ort Nkorongoji gerade an die Personengruppen geraten sind, welche aus historischen Gründen Fulbe negativ gegenüber stehen, während die Mehrheit eher positiv denkt usw.). Die Untersuchung der Wahrscheinlichkeit[6] der Unterschiede gehört zur Analytischen Statistik.
Verweise:
[1] Siehe Kapitel 3.6
[2] Siehe Kapitel 3.3
[3] Siehe Kapitel 3.4
[4] Siehe Kapitel 3.6.1
[5] Siehe Kapitel 2.1.1
[6] Siehe Kapitel 1.3
1.2.2 Analytische Statistik
Die analytische (auch schließende oder deduktive[1] genannt) Statistik beschäftigt sich im Wesentlichen mit der Frage der Zufälligkeit statistisch gemessener Phänomene. So stellt man sich die Frage, inwieweit ein in einer Stichprobe gemessener Mittelwert[2] vom Mittelwert der Grundgesamtheit[3] abweichen[4] könnte; man stellt sich bei verschiedenen Stichproben die Frage, ob sie angesichts ihrer gemessenen Unterschiede noch zur gleichen Grundgesamtheit gehören können u.a. Hier wird also versucht, die untersuchte Stichprobe in einem größeren Ganzen einzuordnen, wobei auch der Untersuchung der Wahrscheinlichkeit von Zusammenhängen[5] bzw. Differenzen breiter Raum eingeräumt wird.
Beispiel 1: Sind Unterschiede (über-)zufällig?
In einem Ort A findet man bei 50 Befragten ein Durchschnittseinkommen von € 1300 ermittelt, im Ort B bei einer gleich großen Stichprobe[6] ein Durchschnittseinkommen von € 1765. Mit Methoden der analytischen Statistik könnten wir herausfinden, ob der Einkommensunterschied zwischen diesen beiden Stichproben die Verallgemeinerung erlaubt, dass die Bevölkerungen der beiden Orte tatsächlich unterschiedlich gut verdienen oder ob der gemessene Unterschied rein zufälliger Natur[7] sein könnte (weil die Befragten sich trotz aller Sorgfalt bei ihrer Auswahl gerade an diesem Punkt von ihren MitbewohnerInnen unterscheiden).
Beispiel 2: Ist ein gemessenes Ergebnis noch ’normal’?
Normalerweise sollten beim Roulette-Spiel in einem längeren Untersuchungszeitraum alle 37 Zahlen etwa gleich häufig auftreten. In einem Spielcasino kamen im Untersuchungszeitraum am Roulette-Tisch verschiedene Zahlen deutlich häufiger als andere vor. Mit den geeigneten (analytischen) Methoden der Wahrscheinlichkeitsrechnung ermittelt man, ob der Roulette-Tisch möglicherweise einseitig so beschaffen oder abgenützt ist, dass man wahrscheinlich auf Dauer mit unterschiedlichen Häufigkeiten rechnen muss oder ob die gemessenen Ergebnisse rein zufälliger Natur waren.
Verweise:
[1] &&& http://www.univie.ac.at/ksa/elearning/cp/qualitative/qualitative-6.html
[2] Siehe Kapitel 3.3
[3] Siehe Kapitel 2.1
[4] Siehe Kapitel 1.3.1
[5] Siehe Kapitel 3.5
[6] Siehe Kapitel 2.1.1
[7] Siehe Kapitel 1.3.2
1.3 Wahrscheinlichkeiten, nicht Gewissheit
(Analytische) Statistik nimmt Wahrscheinlichkeiten an, nicht Gewissheiten.
In der Statistik beschreiben und analysieren wir meist Stichproben[1], also eine Auswahl einer Grundgesamtheit. Dabei ist immer damit zu rechnen, dass sich auch eine sorgfältig zusammengesetzte Stichprobe in wesentlichen Parametern von der Grundgesamtheit[2] unterscheidet, sie also nicht wiederspiegelt.
Wenn wir z.B. 100 Mitmenschen zu ihren Wahlpräferenzen befragen, dann kann es sein, dass die Beliebtheit der SPÖ bei ihnen deutlich anders ausfällt als bei der Grundgesamtheit, auch wenn aus der Schichtung der Stichprobe keinerlei tendenziöse Verteilung der Personen ersichtlich war.
Konfidenzintervalle
Besonders in der analytischen Statistik gibt man daher Konfidenzintervalle bzw. Schwankungsbreiten an, innerhalb derer sich ein wahrer Wert bewegen soll, d.h. der vermutete Wert in der Grundpopulation. Die Breite der Konfidenzintervalle hängt von der Größe der Stichprobe, deren relativer Größe im Verhältnis zur Grundpopulation sowie von der gewählten Irrtumswahrscheinlichkeit ab.
Beispiel Hochrechnung am Wahlsonntag:
Wir erleben dies immer am Wahlsonntag, wenn gegen 17h zum Zeitpunkt der 1. Hochrechnung die Statistikexperten angeben, dass die Partei A mit zwischen 35,3 und 36,8% der Stimmen zu rechnen hat, Partei B etc.
Verweise:
[1] Siehe Kapitel 2.1.1
[2] Siehe Kapitel 2.1
1.3.1 Schwankungsbreiten und Konfidenzintervalle
Unter Schwankungsbreite bzw. Konfidenzintervall versteht man einen Bereich, innerhalb dessen eine Merkmalsausprägung für die Grundpopulation bei einer festgesetzten Irrtumswahrscheinlichkeit angenommen wird, wobei der für die Schätzung verwendete Ausgangswert aus einer Stichprobe ermittelt wurde.
Die Schwankungsbreite oder das Konfidenzintervall hängen von folgenden Faktoren ab:
a. dem gewählten Signifikanzniveau (je signifikanter, dester größer die Schwankungsbreite);
b. dem größenmäßigen Verhältnis zwischen Stichprobe und Grundpopulation[1] (je größer der Unterschied, desto größer die Wahrscheinlichkeit, dass die Ergebnisse voneinander abweichen und damit die Schwankungsbreite);
c. der Größe der Stichprobe[2] (je kleiner, desto größer ist die Schwankungsbreite)
Beispiel zu Punkt b am Wahlabend:
Während die StatistikerInnen gegen 17 h bei vielleicht 10 % der ausgezählten Stimmen die Schwankungsbreite der Stimmen für Partei A mit zwischen 35,3 bis 36,8 angeben (also einer Spanne von 1,5 %), wird gegen 19 h, wenn etwa 90 % der Stimmen ausgezählt sind, eine Schwankungsbreite von vielleicht 0,2 oder 0,3 % angegeben werden, also 35,9-36,2 %).
Siehe auch Konfidenzintervall (Wikipedia)[3].
Verweise:
[1] Siehe Kapitel 2.1
[2] Siehe Kapitel 2.1.1
[3] http://de.wikipedia.org/wiki/Konfidenzintervall
1.3.2 Irrtumswahrscheinlichkeit und Signifikanzniveau
Unter der Irrtumswahrscheinlichkeit p versteht man die zahlenmäßig ausgedrückte Wahrscheinlichkeit, dass sich ein Ergebnis einer statistischen Analyse substantiell vom tatsächlichen Ergebnis der Grundpopulation unterscheidet.
In der Statistik arbeitet man meist mit den drei folgenden Signifikanzniveaus oder -grenzen:
p ≤ 0,05: signifikant (Irrtumswahrscheinlichkeit kleiner als 5 %)
p ≤ 0,01: sehr signifikant (Irrrtumswahrscheinlichkeit kleiner als 1 %)
p ≤ 0,001: höchst signifikant (Irrtumswahrscheinlichkeit kleiner als 1 ‰)
Wenn daher bei einer Hochrechnung am Wahlabend gesagt wird, dass bei einer Irrtumswahrscheinlichkeit von weniger als 1 % eine Partei zwischen 35,2 und 35,6 % der Stimmen erhalten wird, dann bedeutet dies, dass nur in weniger als 1% aller Fälle das tatsächliche Endergebnis außerhalb dieses Bereiches liegen wird.
Siehe auch Signifikanz (Wikipedia)[1].
Verweise:
[1] http://de.wikipedia.org/wiki/Statistische_Signifikanz
2. Von der Fragestellung zur statistischen Analyse
Wesentliche Elemente bei quantitativen Forschungsansätzen
Bei quantitativen Forschungsansätzen sind die folgenden Teilbereiche von besonderer Bedeutung:
- die Untersuchungsobjekte, über welche wir eine Aussage machen möchten (z.B. LateinamerikanerInnen in Wien);
- die Forschungsfrage, die wir mit den Untersuchungsobjekten verbinden (z.B. ihre Erfahrungen in Wien)
- die Operationalisierung, d.h. die Art und Weise, wie wir Einstellungen und Sachverhalte messen
Interessiert uns z.B. die Einstellung der lokalen Bevölkerung zur Entwicklungszusammenarbeit, dann ist das zu untersuchende Objekt die Bevölkerung (die Grundpopulation), während die thematischen Fragen die Einstellungen der Bevölkerung zur EZA darstellen.
Befragung der richtigen Personen mit den richtigen/relevanten Fragen
Wir müssen sowohl sicherstellen, dass wir uns tatsächlich bei unseren Befragungen an diese Grundpopulation wenden (siehe dazu auch Grundpopulation und Repräsentativität[1]), als auch, dass die thematischen Fragen in eindeutiger Weise beantwortet werden können, die eine statistische Interpretation ermöglichen (siehe Operationalisierung[2] und Messen[3]).
Im oben genannten Beispiel müssen wir also genau abklären, wer oder was die lokale Bevölkerung ist, wie sie sich differenziert (Objekt) und zusätzlich eine Reihe von thematischen Fragestellungen entwickeln, deren Gesamtheit es erlaubt, die Einstellung von Menschen zur Entwicklungszusammenarbeit einzuschätzen (wie z.B. prinzipielle Zustimmung bzw. Ablehnung der EZA; Frage nach privaten Spenden oder anderen Aktivitäten für diesen Bereich; Fragen nach der bevorzugten Art der EZA; Frage nach der Akzeptanz von Transfair-Produkten; Fragen nach der gewünschten Höhe der EZA-Leistungen; Fragen nach Ländern und Regionen, die als förderungswürdig gelten usw.).
Verweise:
[1] Siehe Kapitel 2.1.4
[2] Siehe Kapitel 2.2
[3] Siehe Kapitel 2.2.2
2.1 Die Grundpopulation: worüber wir Aussagen machen
Die empirische Grundgesamtheit (Grundpopulation) ist jene abgegrenzte Menge von Personen (z.B. die Wiener Bevölkerung) oder Objekten (z.B. die Regenfälle in einer tropischen Region, die Autos im 7. Bezirk), über die man Aussagen machen möchte.
Anders ausgedrückt: Wenn wir eine Studie zu AfrikanerInnen in Österreich durchführen, dann möchten wir als Ergebnis zu Aussagen kommen, welche Tendenzen sich in dieser Bevölkerungsgruppe zeigen. Alle Mitglieder der Gruppe AfrikanerInnen in Österreich bilden gemeinsam die Grundgesamtheit.
Elemente, Variable und Ausprägungen
Ein Einzelobjekt aus dieser Grundgesamtheit bezeichnet man als statistische Einheit oder Element (z.B. Herr Moussa Bamba aus Bamako, der jetzt in Wien lebt). Die Einzelobjekte weisen jeweils Merkmale auf (auch Variablen genannt, z.B. Geschlecht, Einkommen, Autofarbe etc.), die uns interessieren und über deren Ausprägung in der Grundgesamtheit wir mehr erfahren möchten (die sogenannte Verteilung[1]). Die möglichen Werte dieser Merkmale bezeichnet man als Merkmalsausprägungen. So gibt es für das Merkmal Geschlecht die Ausprägungen männlich oder weiblich, für die Variable Körpergröße Zahlen zwischen theoretisch Null und deutlich über zwei Meter.
Befragung der gesamten Grundpopulation nur selten möglich
Meist ist die Grundpopulation so groß, dass wir nur einen Teil der Grundpopulation befragen können, eine sogenannte Stichprobe.
Öffentliche Quellen für Daten über Grundpopulationen
Grundinformationen über die Verteilung der Grundpopulationen kann man u.a. suchen bei Statistik Austria[2] und anderen Informationsstellen, in einschlägigen Publikationen etc.
Verweise:
[1] Siehe Kapitel 3.1.3
[2] http://www.statistik.at/
2.1.1 Die Stichprobe (Sample)
Eine Stichprobe ist eine Auswahl von Elementen der Grundgesamtheit, anhand derer die Grundgesamtheit[1] nachgebildet werden soll.
Auswahl fast immer notwendig
Auf Grund der Größe der Grundpopulationen ist es kaum jemals möglich, alle Mitglieder derselben zu befragen. Daher greift man in der Regel zu Stichproben, also einer Auswahl von Mitgliedern der Grundgesamtheit. Die Mitglieder der Stichproben sollten in der Regel so ausgewählt sein, dass sie ein unverzerrtes Abbild der Grundgesamtheit darstellen (siehe Repräsentativität[2]).
Verweise:
[1] Siehe Kapitel 2.1
[2] Siehe Kapitel 2.1.4
2.1.2 Teil- oder Vollerhebung?
Teil- oder Vollerhebung?
Je nach Größe der Grundpopulation, der Zahl der BefragerInnen und der finanziellen Ressourcen eines Forschungsprojekts kann eine Stichprobe unterschiedlich groß gewählt werden. Quantitativ sinnvolle Stichprobengrößen beginnen bei einer Befragtenanzahl von 100 und sind auch dann noch von großen Fehlermöglichkeiten gekennzeichnet. Sinnvoller wären auch hier deutlich höhere Stichprobengrößen. Wenn z.B. ein Meinungsforschungsinstitut die Wahlpräferenzen erhebt, befragt es in der Regel 300- 1000 Personen.
Falls die Grundpopulation relativ klein ist, wie z.B. ausländische HändlerInnen am Brunnenmarkt, lässt sich auch eine Vollerhebung durchführen. Dabei werden alle in Frage kommenden Personen befragt.
2.1.3 Die Ziehung (Auswahl) der Stichprobe
Unter Ziehung der Stichprobe versteht man die Selektion der Elemente der Stichprobe.
Die Formen der Ziehung der Stichprobe lassen sich prinzipiell unterteilen in
- Geschichtete Stichprobenauswahl
- Willkürliches Auswahlverfahren
- Zufallsstichproben
- Klumpenstichproben
2.1.3.1 Geschichtete Stichprobenauswahl (Quotenstichprobe)
Unter einer geschichteten Stichprobenauswahl versteht man ein Auswahlverfahren, bei dem wesentliche Verteilungscharakteristiken[1] der Grundgesamtheit[2] nachgebildet werden.
Einzelne für die Untersuchung als relevant erachtete Merkmale der Zielgruppe werden annähernd im gleichen Verhältnis auf die Stichprobe übertragen, wie sie in der Grundgesamtheit vorkommen.
Relevant sind besonders die Merkmale, welche bei der spezifischen Fragestellung zu besonderer Differenzierung führen können. Bei den Wahlpräferenzen sind das z.B. das Bundesland (Wien ist z.B. traditionell ein ’rotes’ Bundesland, NÖ ein ’schwarzes’); Geschlecht (Frauen haben oft ein ganz anderes Wahlverhalten als Männer); Alter (die Älteren haben eine stärkere Tendenz zur SPÖ, die Jüngeren zu den Grünen) etc.
Beispiel:
Man versucht die aktuellen Wahlpräferenzen der Österreicher mit insgesamt 500 Befragten zu erheben. Da etwa 1/5 der ÖsterreicherInnen in Wien lebt, sollte dementsprechend auch 1/5 der Befragten der Stichprobe, also ca. 100 Personen, aus Wien kommen, aber wesentlich weniger aus dem Burgenland. In gleicher Weise sollte auch die altersmäßige Verteilung der ÖsterreicherInnen wiedergegeben werden, also etwa 1/4 der Befragten über 60 Jahre etc.
Je nachdem, ob die wesentliichen Verteilungsparameter berücksichtigt werden oder einzelne teilweise bewusst verzerrt werden, spricht man von proportional geschichteten Stichproben oder von disproportional geschichteten Stichproben.
Verweise:
[1] Siehe Kapitel 3.1.3
[2] Siehe Kapitel 2.1
2.1.3.1.1 Proportional geschichtete Stichproben
Bei der proportional geschichteten Stichprobe werden die Schichten entsprechend ihrer Verteilung in der Grundgesamtheit ausgewählt. Es wird ein durchgehend treues und unverzerrtes Abbild der Grundgesamtheit angestrebt.
Besonders häufig werden für die Schichtung Geschlecht, Alter und Wohnart verwendet.
2.1.3.1.2 Disproportional geschichtete Stichproben
Unter einer disproportional geschichteten Stichprobe versteht man die bewusste Verzerrung einzelner Verteilungsparameter, um signifikante Aussagen über Randbereiche erhalten zu können. Dabei wird eine Bevölkerungsgruppe überproportional wiedergegeben, um genügend Interviews für sie zu erhalten.
Diese Methode wird v.a. angewandt, um bei beschränkten Stichprobengrößen signifikante[1] Aussagen über kleinere Bevölkerungsgruppen erhalten zu können, die für die Fragestellung besonders interessant sind.
Beispiel: Umfrage zu Reformen im Bildungsbereich
Problemstellung: Man möchte herausfinden, wie die österreichische Bevölkerung eine große Bildungsreform einschließlich des Hochschulwesens einschätzt. Man kann dabei insgesamt 1000 Personen befragen. Befragt man die österreichische Bevölkerung proportional geschichtet, würde man etwa 27 Studierende zu diesem Thema befragen, da mit etwa 220.000 Studierenden an öffentlichen Hochschulen ihr Anteil an der Bevölkerung bei ca. 2,7 % liegt. Man könnte somit bei bloß 27 befragten Studierenden keine verlässliche Aussage über sie bekommen, da ihre spezifische Anzahl zu klein ist. Da sie als Betroffene jedoch für die Fragestellung von besonderer Relevanz sind, könnte man sie übergewichten und 100 oder mehr von ihnen befragen.
Vorteil Kenntnis von Randbereichen, Nachteil Verzerrung des Meinungsbildes
Der Vorteil liegt in einer besseren Kenntnis des Meinungsbilds dieser thematisch wichtigen Subgruppe, der Nachteil dieser Methode in einem Verlust an Repräsentativität. Die Stichprobe ist verzerrt. Wollte man nun allgemeine Aussagen über das Meinungsbild bezüglich dieser Bildungsreform in der österreichischen Öffentlichkeit treffen, müsste man das Meinungsbild der Studierenden auf ihren tatsächlichen Anteil in der Bevölkerung hinuntergewichten.
Verweise:
[1] Siehe Kapitel 1.3.2
2.1.3.1.3 Laufende Kontrolle der Schichtung
Während der Befragungsphase laufende Kontrolle der Schichtung erforderlich
Bei einem quantitativen Forschungsprojekt führt man laufend Erhebungen, meist mit Fragebögen, durch. Dabei muss man stets einen Überblick über die Verteilung[1] der bereits Interviewten haben, um Abweichungen von der Verteilung in der Grundpopulation[2] korrigieren zu können. Wie? Indem man die nächsten Interviewten aus Personengruppen wählt, die bisher unterrepräsentiert waren, deren bisheriger Anteil in der Stichprobe also deutlich geringer als ihr Anteil in der Grundpopulation ist.
Berechnung
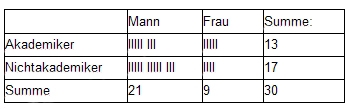
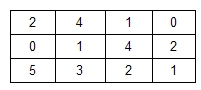
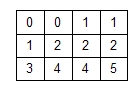
Bei ganz kleinen Umfragen kann man die Aufteilungsverhältnisse mit einer Matrix kontrollieren, in die man laufend mit ‚Stricherln’ einträgt, wen man interviewt hat. Nehmen wir an, in der Grundpopulation hätten wir eine Verteilung von 55 % Männern und 45 % Frauen bzw. von 25 % AkademikerInnen und 75 % NichtakademikerInnen. Mit den Schichtungsfragen stellen wir fest, ob die Verteilung der Interviewten mit der der Grundpopulation übereinstimmt. Daher müssen Schichtungsfragen auch fester Bestandteil der Fragebögen sein. Bisher haben wir folgende Interviews geführt:
In unserer Stichprobe findet sich bisher ein Männeranteil von 70 % (gegenüber 55 % in der Grundpopulation) sowie ein AkademikerInnen-Anteil von 43 % (gegenüber 25 % in der Grundpopulation). Daher müssen wir in Zukunft mehr Frauen und mehr NichtakademikerInnen befragen, solange, bis dieses Ungleichgewicht behoben ist. Zusätzlich gilt es zu bedenken, dass in unserer Stichprobe der Akademikeranteil bei den Männern bisher bei ca. 38 % liegt, der Akademikerinnen-Anteil bei den Frauen jedoch bei ca. 55 %. Sofern beide in der Grundpopulation den gleichen AkademikerInnen-Anteil aufweisen, müssten wir bei den folgenden Interviews darauf achten, dass bei Frauen noch stärker als bei den Männern besonders NichtakademikerInnen interviewt werden.
Verweise:
[1] Siehe Kapitel 3.1.3
[2] Siehe Kapitel 2.1
2.1.3.2 Zufallsstichproben
Unter Zufallsstichproben versteht man Auswahlverfahren einer Stichprobe, bei welchen bei einem theoretisch vorliegenden Register aller Elemente der Grundgesamtheit[1] die Elemente der Stichprobe zufällig gezogen werden.
Man vergleiche dies mit einer Lottoziehung. Man hat ein Register von 45 Lotto-Zahlen, welche die gleiche Ziehungwahrscheinlichkeit aufweisen. Aus diesen werden beim Lotto insgesamt sechs Zahlen gezogen.
Man unterscheidet zwischen einfachen und systematischen Zufallsstichproben. Eine Sonderform der Zufallsstichproben sind die geschichteten Zuallsstichproben.
Allgemeines Problem von Zufallsstichproben:
Es ist äußerst schwierig, Register aufzutreiben oder zu erstellen, welche tatsächlich jedem Element der Grundgesamtheit die gleiche Chance des Gezogenwerdens erlauben. Im Telefonregister scheinen viele Nummern nicht auf, da sie als Geheimnummern unterdrückt werden. Geheimnummern werden wiederum häufiger von besser etablierten Personen verwendet, weshalb sie über das Telefonregister eine geringere Chance haben, erreicht zu werden.
Verweise:
[1] Siehe Kapitel 2.1
2.1.3.2.1 Einfache Zufallsstichprobe
Bei der einfachen Zufallsstichprobe gibt es keinerlei Systematik der Ziehung.
Will man z.B. die Wiener Bevölkerung zum Thema Stadtautobahn befragen, könnte man alle Telefonnummern in einen PC einspeisen (das Register) und sich von einem Programm mit Zufallsgenerator 100 dieser Telefonnummern ’auswerfen’ lassen.
2.1.3.2.2 Systematische Zufallsstichprobe
Bei der systematischen Zufallsstichprobe erfolgt die Ziehung mit System, mit einem bestimmten Ziehungsschlüssel, und damit nicht mehr ganz zufällig.
Beispiel:
Man möchte die Einstellung der Wiener Bevölkerung zur Fristenlösung befragen. Man nimmt das Telefonbuch der Stadt Wien und wählt jede 100. Telefonnummer an.
Potentielle Probleme der systematischen Zufallsstichproben:
Ein Problem dieses Verfahrens kann in einer nicht erkannten Systematik der Verteilung liegen. Wenn man alle Personen befragt, welche jeweils die Türnummer 1 in den Häusern aufweisen, dann wäre die Wahrscheinlichkeit groß, dass Hausmeister deutlich überrrepräsentiert sind.
Systematik darf nicht zu starr sein:
Daher sollte die Systematik nicht zu starr sein. Man könnte z.B. bei der ersten Befragung im 1. Haus das Alter der Person abfragen und aus dem Alter die Türnummer des nächsten abzufragenden Hauses ermitteln, z.B. aus der Ziffernsumme. Nehmen wir an, ein Alter von 32 wird angegeben, dann ist die Ziffernsumme 3+2 = 5, beim nächsten Haus wird also die BewohnerIn der Türnummer 5 befragt usw.
2.1.3.2.3 Geschichtete Zufallsstichprobe
Eine Sonderform der Zufallsstichprobe ist die geschichtete Zufallsstichprobe. Bei dieser findet zuerst eine Einteilung der Stichprobe in sich nicht überlappende Schichten statt. Aus diesen werden wiederum einfache oder systematische Zufallsstichproben entnommen.
Beispiel: Befragung von WienerInnen
Man entscheidet sich zuerst für eine Berücksichtigung der Größenverhältnisse der einzelnen Bezirke, danach realisiert man mit der festgelegten Anzahl von Personen aus diesen Bezirken einfache oder systematische Zufallsstichproben.
2.1.3.3 Willkürliches Auswahlverfahren
Unter einem willkürlichen Auswahlverfahren versteht man eine unkontrollierte Form der Ziehung, bei welcher die Elemente der Grundgesamtheit eine deutlich unterschiedliche Wahrscheinlichkeit der Selektion aufweisen, weshalb von der Stichprobe nicht mehr auf die Grundgesamtheit geschlossen werden kann.
Beispiel:
Eine LehrerIn fragt in der Schule, welche SchülerInnen sich bereit erklären, bei einem sportlichen Ausdauertraining mit Vor- und Nachtest mitzumachen. Eine kleine Zahl von SchülerInnen meldet sich, die wahrscheinlich um einiges fitter als die anderen sind.
Sinnvoll für Rückschlüsse auf Methoden
Auch eine derartige Auswahl kann sinnvoll sein, wenn man z.B. messen möchte, ob sich die Fitness der ausgewählten TeilnehmerInnen durch das Training verbesserte. In der Medizin verwendet man oft dieses Auswahlverfahren, um die Wirksamkeit von Medikamenten zu testen.
Kein Rückschluss auf die Grundgesamtheit
Ein Rückschluss auf die Grundgesamtheit ist jedoch mit dem willkürlichen Auswahlverfahren nicht erlaubt.
2.1.3.4 Klumpenstichproben
Unter einer Klumpenstichprobe versteht man die Auswahl von Klumpen (Bündel von Erhebungselementen wie Schulklassen oder Unternehmen) nach dem Zufallsverfahren.
Dieses Auswahlverfahren erfolgt meist aus Gründen der Ökonomie. Statt einzelne SchülerInnen aus Schulen in 1000 Orten zu befragen, befragt man z.B. alle SchülerInnen aus 30 ausgewählten Orten, von denen man annimmt, dass diese bezüglich ihrer Eigenheiten die Grundgesamtheit der Orte abbilden.
2.1.4 Repräsentativität
Unter Repräsentativität versteht man die angestrebte Eigenschaft von statistischen Erhebungen, die Grundgesamtheit in der ausgewählten Stichprobe möglichst unverzerrt nachzubilden. Eine statistische Erhebung ist repräsentativ, wenn sie auf einer Zufallsstichprobe basiert und Aussagen über die Grundgesamtheit[1] zulässt.
Damit von der Stichprobe auf die Grundgesamtheit geschlossen werden kann, müssen bei den verschiedenen Formen der Ziehungen folgende Bedingungen erfüllt sein:
- Die Grundgesamtheit muss exakt definiert sein. Es muss somit klar festgelegt werden, welche Elemente zur Stichprobe gehören. Gehören z.B. bei einer Untersuchung über AfrikanerInnen in Österreich auch hier geborene Kinder von ZuwanderInnen zur Grundgesamtheit oder ausschließlich in Afrika Geborene?
- Die Grundgesamtheit muss physisch oder symbolisch präsent und manipulierbar sein (sie muss sich durchmischen lassen, jedes Element muss entnehmbar sein). Einfaches Beispiel: Bei einer Lottoziehung wären 45 Kugeln vorhanden, aus denen nach dem Zufallsprinzip jeweils eine gezogen wird.
- Jedes Element darf nur einmal in der Grundgesamtheit vertreten sein. Man darf also nicht z.B. die gleiche Person zweimal mit dem gleichen Fragebogen befragen.
- Die Auswahl muss so erfolgen, dass jedes Element die gleiche berechenbare Auswahlchance (größer 0) hat, in die Stichprobe zu gelangen. Wenn die Befragung ausschließlich an Orten oder zu Zeitpunkten stattfindet, an welchen ein Teil der Grundpopulation nicht oder nur selten erreichbar ist (z.B. ältere Menschen in Discos oder Arbeitende untertags im Park), dann ist die Repräsentativität ebenfalls nicht gewährleistet.
Verweise:
[1] Siehe Kapitel 2.1
2.1.5 Was tun, wenn die Grundpopulation nicht bekannt ist?
Sollte es unmöglich sein, statistische Daten über die Schichtung der Grundpopulation[1] zu erhalten, kann man entweder
- aufgrund vermutlich vergleichbarer Grundpopulationen verallgemeinern. Nehmen wir an, wir kennen den Frauenanteil von SudanesInnen in Wien nicht, Die ZuwanderInnen aus verschiedenen anderen vergleichbaren afrikanischen Ländern (islamisch, arabisch - englisch) weisen einen Frauenanteil von etwa 40 % auf, dann könnte man auch bei Sudanesinnen diesen Wert als Arbeitshypothese ansetzen. Man sollte jedoch unbedingt in der Publikation auf dieses Problem und die daraus folgende Annahme einer bestimmten Schichtung hinweisen.
- ExpertInnen zum Thema befragen, am besten gleich mehrere. Z.B. könnte man das Magistrat befragen, in welchem Ausmaß verschiedene Nationalitäten am Brunnenmarkt vertreten sind; IntegrationsforscherInnen, auch erfahrene Mitglieder der Grundpopulation etc.
Verweise:
[1] Siehe Kapitel 2.1
2.2 Die Operationalisierung
Unter Operationalisierung versteht man die präzise Angabe der Vorgangsweise, mit der ein theoretisches Konstrukt gemessen werden soll (wie z.B. die Akzeptanz von Zuwanderergruppen). Dazu gehört die Auswahl der Indikatoren, die genaue Formulierung der Fragen im Fragebogen, dazu gehören die Antwortkategorien, die Bestimmung der Messinstrumente, die Bestimmung der Genauigkeit der Messung, die Anweisungen an die InterviewerInnen, wie sie die Fragen stellen und welche Zusatzinformationen sie geben dürfen etc. Operationalisierung[1] versucht also bis ins kleinste Detail sicherzustellen, dass die wissenschaftlichen Qualitätserfordernisse[2] für vergleichbare Forschungsarbeiten eingehalten werden können und tatsächlich brauchbare Antworten zu den Themen gefunden werden können, die man zu untersuchen vorgibt.
Was man untersucht bzw. ’misst’, muss in seinen Ausprägungen in sinnvolle und voneinander abgrenzbare Untereinheiten unterteilt werden können.
Untersucht man z.B. die mathematischen Fähigkeiten von Schulkindern, kann man zur Notenskala greifen. Das Geschlecht kann in männlich und weiblich unterteilt werden. Bei der Untersuchung der Körpergröße wird man in Maßeinheiten wie cm oder mm messen. Die Einstellung gegenüber Zuwanderergruppen können wir z.B. in einer fünfteiligen Abstufung wiedergeben, wie z.B. ’sehr positiv’, ’eher positiv’, ’neutral’, ’eher ablehnend’ oder ’absolut ablehnend’. Den Erfolg bei den Bewerbungen von Zuwanderern am Arbeitsmarkt könnte man unterteilen in ’sofort abgelehnt’, ’zu Bewerbungsgespräch eingeladen, aber dann abgelehnt’ und ’aufgenommen’ unterteilen. Den Familienstand kann man in ’ledig’, ’geschieden’, ’verheiratet’, ’verwitwet’ unterteilen.
Verweise:
[1] &&& http://www.univie.ac.at/ksa/elearning/cp/ksamethoden/ksamethoden-43.html
[2] Siehe Kapitel 2.3
2.2.1 Die Suche nach Indikatoren
Im Forschungsentwurf werden verschiedene Hypothesen formuliert. Nun benötigt man eine Reihe von Indikatoren, um die Hypothesen[1] beibehalten bzw. verwerfen zu können.
In vielen Fällen ist die Suche nach den Indikatoren einfach. Möchte man z.B. ermitteln, wie warm zur gleichen Jahreszeit verschiedene Orte sind, dann genügt eine Messung mit dem Thermometer. Meist jedoch sind die Forschungsfragen komplexer und nicht mit einer einzigen konkreten Messungsart zu beantworten.
Beispiel 1:
Nehmen wir an, Sie postulieren, dass die Gesellschaft in Nepal sehr ungleich und damit nicht egalitär ist. Nun bräuchten wir eine Reihe von sehr viel spezifischeren Fragestellungen, eigentlich Subhypothesen, deren Synthese zur Beantwortung der allgemeinen Hypothese führen kann. Wir könnten zwischen materieller, rechtlicher und politischer (Un-)Gleichheit unterscheiden. Wir könnten Vermögensverhältnisse in verschiedenen Schichten betrachten; den Zugang zu staatlichen und privaten Ressourcen; wir könnten die Vertretung verschiedener Gruppen der Gesellschaft (Frauen, Adelige, Bauern etc.) im Parlament und anderen öffentlichen Gremien betrachten. Wir könnten die Schulbesuchsquote kontrastiv untersuchen etc.
In all diesen Punkten müssen wir äußerst konkret und präzise werden. Bezüglich des Schulbesuchs könnte man die Zahl der Jahre in der Schule, den maximalen Ausbildungsgrad etc. abfragen. Bezüglich des Vermögens Grundstücke, Häuser, Kapital, Vieh, andere Besitztümer, Leibeigene etc. Wir könnten Einschätzungen abfragen, ob Heiraten zwischen Adeligen und Nichtadeligen als akzeptabel empfunden werden, ob die Befragten annehmen, dass Arme und Reiche vor Gericht die gleichen Chancen haben usw.
Beispiel 2:
Sie nehmen an, dass viele Menschen in Wien AraberInnen ablehnen und oft sogar rassistisch gegenüberstehen. Sie könnten nun in einem Fragebogen an die Wiener Bevölkerung die Wertschätzung des Islams, der arabischen Kultur abfragen. Sie könnten fragen, in welchem Maße man annimmt, dass AraberInnen besonders leicht zu Terrorismus neigen. Sie könnten fragen, ob man sich vorstellen könnte, AraberInnen als angeheiratete Familienmitglieder zu akzeptieren. Sie könnten die Bereitschaft abfragen, AraberInnen Wohnungen zu vermieten. Sie könnten die Befragten ersuchen, die ersten Assoziationen zu nennen, die ihnen beim Begriff AraberInnen einfallen. Sie könnten die Befragten ersuchen, Ihnen das dominante Gefühl zu nennen, welches sie in Gegenwart von AraberInnen spüren usw.
Letztendlich könnte man sich auf einen Schlüssel einigen, mit welchem Anteil die mit den verschiedenen Detailfragen erhaltenen Informationen in einen Sammelparameter (Beispiel 1: Ungleichheit/Gleichheit; Beispiel 2: Rassismus gegenüber AraberInnen) einfließen.
Verweise:
[1] &&& http://www.univie.ac.at/ksa/elearning/cp/ksamethoden/ksamethoden-49.html
2.2.2 Das Messen
Unter Messung versteht man die quantitative Bestimmung von Sachverhalten in Form einer Messgröße. d.h. wir ordnen diesen Zahlen zu.
Misst man die Temperatur eines Körpers, wird man in unseren Regionen in der Messgröße Celsius messen, in anderen in Fahrenheit etc. Messen wir die Körpergröße, dann messen wir bei größeren Körpern in Metern und Zentimetern, bei Kleinstlebewesen aber auch in Millionstel Metern und darunter. Messen wir das Haushaltseinkommen, werden wir in Euro messen. Bei der Messung von Einstellungen und sozialen Sachverhalten kann man selbst die Messgrößen bestimmen. So könnte man bei der Einschätzung der Sympathie für eine bestimmte Kultur fünf verschiedene Messgrößen festlegen, wie z.B. ’sehr sympathisch’, ’sympathisch’, ’neutral’, ’weniger sympathisch’ und ’unsympathisch’.
Die Antwortkategorien müssen fair und ausgewogen sein
Es wäre tendenziös und unseriös, in der obigen Sympathie-Skala im positiven Bereich nur ’sehr sympathisch’ anzugeben, im negativen jedoch die zwei vorhandenen Unterscheidungen. Dies könnte dazu führen, dass Antwortende, die nur eine leichte Sympathie für die andere Kultur empfinden, zum neutralen Wert ausweichen. Daher gilt als Grundregel, dass die Zahl der möglichen Antwortvarianten bei derartigen Fragen im negativen Bereich genauso hoch wie im positiven Bereich sein soll.
Messungen beinhalten immer das Problem von Messfehlern.
2.2.2.1 Messfehler
Unter Messfehler versteht man die Abweichung des Ergebnisses von Messungen von den realen Gegebenheiten. Wo eine Messung erfolgt, sollte man immer die Möglichkeit von Messfehlern berücksichtigen. Man kann zwischen zufälligen, systematischen und fahrlässigen Messfehlern unterscheiden.
A. Zufällige Messfehler:
Zufällige Messfehler sind von den Messenden nicht zu kontrollieren. Wenn man zum Beispiel eine bestimmte Personengruppe zu einem sensiblen Thema befragen möchte und gerade am Tag vorher ein (den InterviewerInnen unbekanntes) Ereignis eintritt, welches ihre Neigung zu ehrlichen Antworten temporär verändert, während bei Vergleichsgruppen im gleichen Zeitraum nichts Vergleichbares auftritt, können verfälschte Ergebnisse auftreten. Misst man die Regenfälle in der Sahelgegend, kann es sein, dass ein Ort deutlich besser und gleichmäßiger beregnet wird, als die nicht gemessenen Nachbarorte, im nächsten Jahr kann es umgekehrt sein. Es gibt jedoch einen sogenannten Zentralen Grenzwertsatz der Statistik (Wikibooks)[1], nach welchem zufällige Fehler sich im Laufe der Zeit ausgleichen und einer Normalverteilung zustreben. Man kann daher postulieren, dass die zufälligen Messfehler bei häufigen Messungen zum Ausgleich tendieren.
B. Systematische Messfehler:
Systematische Messfehler können durch fehlerhafte Messgeräte entstehen, wie z.B. die Gewichtsmessung durch eine verstellte Waage; die Zeitmessung durch eine ungenaue Uhr; aber auch z.B. eine Kommunikationsform, welche den Zugang zu manchen Informationen kaum erlaubt. So ist es möglich, dass besonders hoch emotionale Angelegenheiten in einer Fremdsprache zu anderen Antworten als in seiner Muttersprache führen. Man überlege sich, ob es einem in einer Fremdsprache ähnlich schwer wie in seiner Muttersprache fällt, z.B. Ich liebe Dich zu sagen, wo beim Aussprechen ähnlicher Sätze auch Assoziationen mit Enttäuschungen u.a. verbunden sein können und damit auch die Angst vor Zurückweisung.
Ein Teil der systematischen Messfehler kann durch stetige Kontrolle und kritische Hinterfragung der Messinstrumente behoben werden.
C. Fahrlässige Messfehler:
Grobe Messfehler beruhen auf menschlichen Fehlern. Man trägt z.B. beim Alter 15 statt 51 ein, schreibt eine Antwort in die falsche Spalte; vergisst eine Frage zu stellen oder zu beantworten. Man vermittelt beim Interview eigene Einstellungen, welche mit großer Wahrscheinlichkeit zu einer veränderten Reaktion des Befragten führen (wenn man z.B. einem Befragten deutlich zeigt, dass man seine Einstellungen und Meinungen geringschätzt).
Weiterführendes zu Messfehlern:
Messfehler (Wikipedia)[2]
Verweise:
[1] https://de.wikibooks.org/wiki/Statistik:_Zentraler_Grenzwertsatz
[2] http://de.wikipedia.org/wiki/Messfehler
2.2.3 Vom Fragebogen zum Codeplan
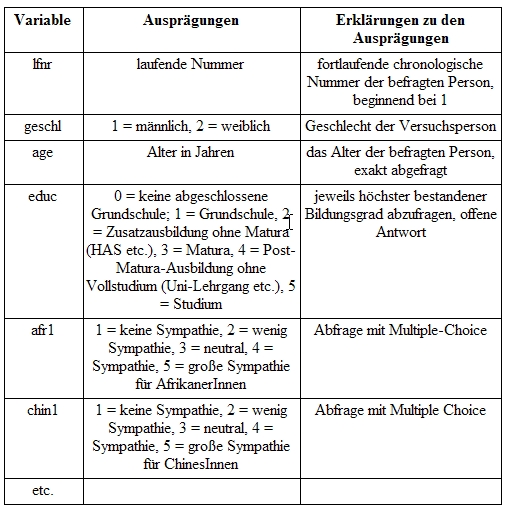
Unter einem Codeplan verstehen wir die Auflistung aller verwendeten Variablen mit einer eindeutigen Information zur inhaltlichen Bedeutung der numerischen Codes, eventuell noch von weiteren Informationen begleitet, welche sich auf den Messvorgang beziehen.
In einem Codeplan halten wir eindeutig fest, welchen Variablennamen Fragen des Fragebogens entsprechen, wie verschiedene Ausprägungen von Variablen gemessen werden (z.B. in cm für die Körpergröße oder in Ja/Nein für bestimmte Erfahrungen) und wie diese Ausprägungen in eine numerische Form übersetzt werden, was überhaupt erst eine maschinelle quantitative Analyse erlaubt.
Statistikprogramme benötigen automatisch interpretierbare Datentypen
Statistikprogramme benötigen für Berechnungen bestimmte Datentypen, die in der Regel numerisch sind. Kein Statistikprogramm kann in den Antwortkategorien ’sehr’, ’eher schon’, ’durchschnittlich’, ’eher weniger’, ’überhaupt nicht’ eine logische Reihe erkennen, dass also diese Bezeichnungen für verschiedene logische Abstufungen stehen, nämlich für eine Ordinalskala[1].
Damit ein Statistikprogramm wie SPSS die logische Reihenfolge erkennen und danach Analysen über diese bilden kann, müssen die Textwerte in numerische umcodiert werden. Im Codeplan, d.h. der Dokumentation über die ursprünglichen Text- Begriffe und ihrer numerischen Entsprechungen, werden diese Umcodierungen festgehalten. Im obigen Beispiel könnte man ’sehr’ immer durch 1, ’eher schon’ durch 2, ’durchschnittlich’ durch 3, ’eher weniger’ durch 4 und ’überhaupt nicht’ durch 5 ersetzen. Nun ist eine für die Software durchgehende Reihe von 1-5 entstanden, die vom kleinsten zum größten Wert gereiht ist.
Aktuelle Statistikprogramme wie SPSS rechnen intern mit diesen numerischen Daten, können mit einfachen Befehlen jedoch bei der Ausgabe der Ergebnisse automatisch die urspünglichen Textinformationen verwenden.
Beispiel eines Codeplans:
Verweise:
[1] Siehe Kapitel 3.1.2.3
2.2.3.1 Dateneingabe und Erstellung einer Datenmatrix
Unter einer Datenmatrix versteht man eine Tabelle, in welcher alle Messungen an den Versuchsobjekten zusammengefasst werden. Die Daten sind normalerweise so angeordnet, dass jede Zeile der Datenmatrix alle Messungen an einem einzelnen Datenobjekt enthält. In den Zeilen stehen somit von links nach rechts die Angaben zu einer Person (bzw. zu den Untersuchungsobjekten), während in den Spalten die Variablen eingetragen werden.
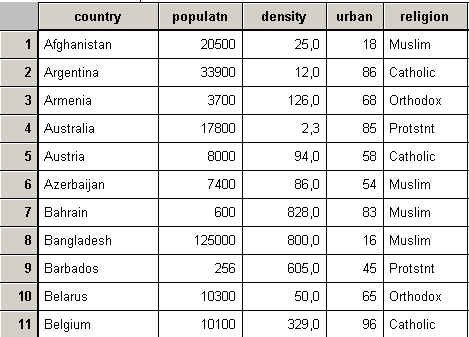
Siehe z.B. die ersten Spalten und Zeilen der SPSS-Datei zur weltweiten Entwicklung world95.sav:
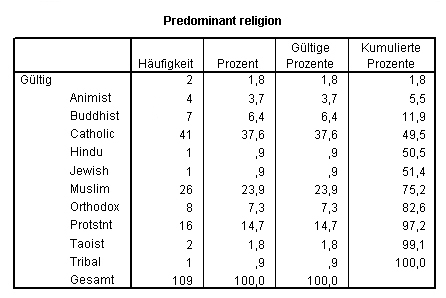
Die Untersuchungsobjekte sind hier eindeutig durch ihre in der ersten Spalte stehenden (Länder-)Namen identifiziert. Von links nach rechts werden danach in den einzelnen Zeilen durch Variable Informationen zu den jeweiligen Ländern angegeben: Bevölkerungsgröße, Bevölkerungsdichte, Prozentsatz der städtischen Bevölkerung, Religion etc.
Es ist äußerst empfehlenswert, die Datenmatrix in der hier beschriebenen Weise zu verwalten, da alle führenden und gängigen Analyse- und Darstellungsprogramme (Excel, SPSS etc.) die gleiche Anordnung verwenden.
2.2.3.2 Umcodierung mit SPSS
SPSS benötigt gleichzeitig für viele Funktionen numerische Daten, wo Daten in String (oder Text-)Format vorliegen. So kann SPSS bei reinen Textdaten, wie z.B. ’Sehr Gut’ oder ’Gut’ nicht erkennen, dass ’Sehr Gut’ eine höhere Intensität bzw. Qualität als ’Gut’ wiederspiegelt. SPSS würde eine sinnvolle Rangfolge jedoch in numerischer Form erkennen.
SPSS erlaubt es, Stringvariable automatisch in numerische zu codieren.
Dazu benützen Sie die Funktion TRANSFORMIEREN - UMCODIEREN in der Menüleiste. Nun können Sie sich entscheiden, ob die Umcodierung in die gleiche oder in eine andere Variable erfolgen soll. Es ist besser, sich für eine andere Variable zu entscheiden, da durch die Umcodierung (man kann auch mehrere Werte zu einem einzigen neuen umcodieren) Informationsverlust auftreten kann (ob willentlich oder durch einen Bedienungsfehler). Dieses Problem wird durch Umcodierung in eine neue Variable ausgeschlossen.
Sie wählen nun die Variable aus, welche umcodiert werden soll und geben im Feld Ausgabevariable einen neuen Namen dafür ein (der aus Gründen verschiedenster Kompatibilität) acht Zeichen nicht überschreiten darf. Im Feld darunter können Sie jedoch einen beliebig langen und expressiveren Namen wählen.
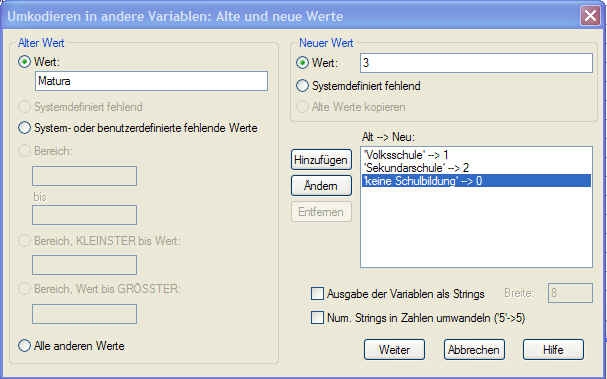
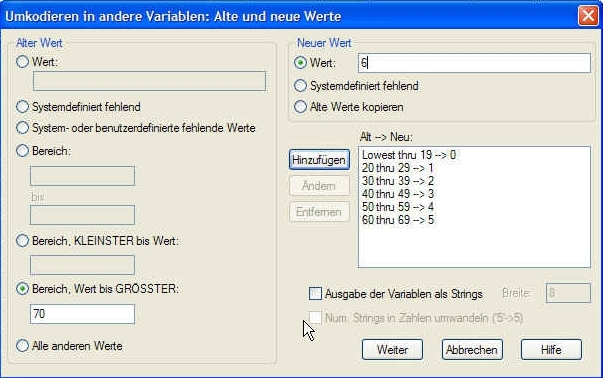
Klicken Sie nun auf Alte und neue Werte. Wenn Sie einzelne Werte umcodieren möchten, geben Sie im Feld Wert denselben ein (z.B. Matura). Nun benötigen Sie einen neuen Wert dafür. Dafür könnten Sie z.B. die Zahl 3 im Feld Neuer Wert eingeben. Im oben angeführten Beispiel wären verschiedene abgeschlossene Ausbildungsstufen in eine logische Reihenfolge gebracht.
Falls Sie mehrere (numerische) Werte zu einem einzigen neuen zusammenfassen möchten, können Sie einen Bereich angeben (z.B. Bereich 20 bis 29), wenn Sie alle zwischen 20-29jährigen in eine einzige Altersklasse ’zwischen 20 und 30' einbringen möchten). Klicken Sie nach jeder einzelnen Angabe zur Umcodierung auf Hinzufügen.
Klicken Sie am Ende auf Weiter und dann auf OK. Ihre Daten werden nun in die neue Variable umcodiert. Erst jetzt wäre es Ihnen möglich, dass SPSS die Ausbildung nach Jahren und Qualität sinnvoll reihen kann und natürlich auch viele weitere (damit zusammenhängenden) Analysen rechnen kann. So wäre erst jetzt die Berechnung einer Korrelation[1] zwischen dem Ausbildungsgrad und dem Einkommen möglich.
Verweise:
[1] Siehe Kapitel 3.5.3
2.2.3.3 Automatische Rückcodierung mit SPSS
Damit SPSS mit Daten rechnen kann, wurden diese in numerischer Form eingegeben oder in eine neue numerische Variable umcodiert. Wenn Sie nun eine auf diesen neuen Variablen basierende Analyse starten, wirken die Ergebnisse ohne zusätzliche Information wenig informativ.
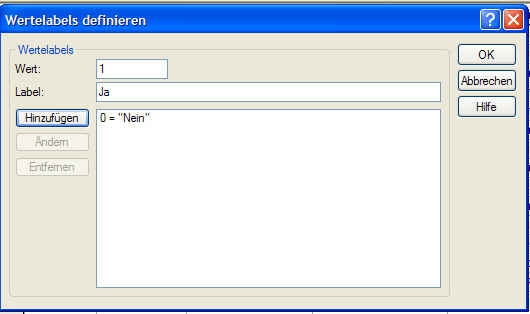
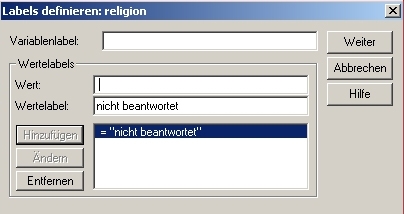
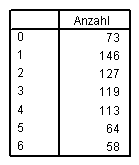
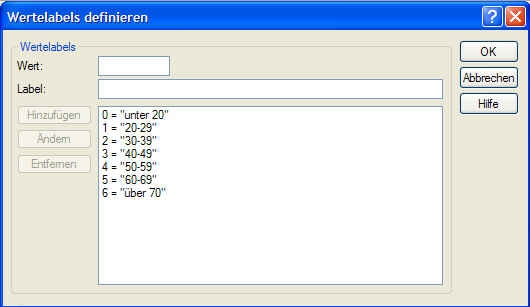
Niemand könnte ohne Zusatzinformation wissen, dass 0 für Nein und 1 für Ja steht. Damit SPSS intern mit den numerischen Daten rechnen kann, wir jedoch bei allen Ausgaben (Diagramme, Analysen etc.) informative Bezeichnungen erhalten, klicken wir in SPSS unten links auf die Variablenansicht. Im neuen Fenster finden wir in der Zeile der neuen Variable den Punkt Variablenlabel. Nach Doppelklick darauf erscheint folgendes Fenster:
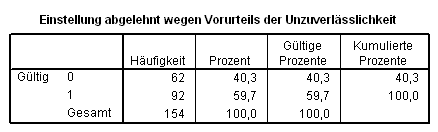
Wir geben nun für den Wert das gewünschte Label ein. Wir möchten, dass statt 0 der aussagekräftige Text Nein erscheint, statt 1 der aussagekräftige Wert Ja. Nach Eingabe aller automatisch durchzuführenden Änderungen klicken wir auf OK.
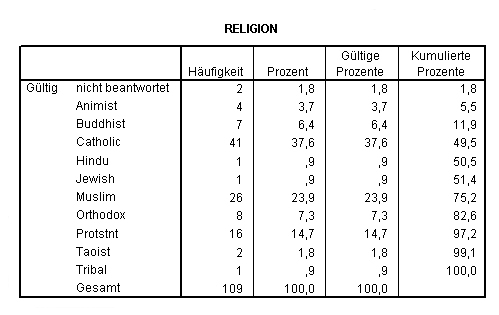
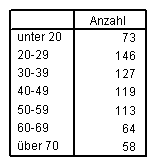
Wenn wir nun die gleiche Häufigkeitsberechnung wie oben durchführen, erhalten wir nun folgende leichter verständliche Tabelle:
2.3 Gütekriterien quantitativer Untersuchungen
Statistische Untersuchungen müssen wie jede andere Form wissenschaftlicher Betätigung den Kernansprüchen[1] der Reliabilität, der Validität und der Objektivität genügen:
Reliabilität:
Unter Reliabilität oder Zuverlässigkeit versteht man die formale Genauigkeit wissenschaftlicher Untersuchungen. Darunter versteht man, dass die Untersuchungen mit einem Höchstmaß an Anstrengungen verbunden werden, Messfehler jeder Art auszuschließen. Reliabilität ist somit ein Indikator für die Replizierbarkeit (Wiederholbarkeit) der Ergebnisse. Fragen müssen z.B. so eindeutig formuliert sein, dass sie nicht höchst unterschiedlich verstanden werden können.
Validität:
Validität liegt vor, wenn wenn die gewählten Indikatoren, Fragen und Antwortmöglichkieten wirklich und präzise das messen, was gemessen werden soll.
Wenn man die Frage stellt, ob der Proband Schweinefleisch isst, so ist die Verneinung noch keineswegs ein Beweis dafür, dass er Vegetarier ist, sondern nur, dass er eben Schweinefleisch aus verschiedenen Gründen nicht mag. Wäre die Frage nach dem Essen von Schweinefleisch die einzige auf Fleisch bezogene Frage im Fragebogen, so wäre der Fragebogen nicht valide, um auf Vegetarismus zu schließen.
Objektivität:
Die Objektivität von Messverfahren und Fragen ist weitgehend gewährleistet, wenn die Wahl der Messenden, InterviewerInnen, PrüferInnen keinen Einfluss auf die Ergebnisse hat.
Objektivität wäre z.B. zweifelhaft, wenn man verunsicherte Männer mit einem persönlich überreichten Fragebogen zu ihrem Sexualleben einmal von ebenfalls verunsicherten Männern und das andere Mal von jungen, attraktiven und selbstbewussten Frauen befragen lassen würde, wobei die Fragen von den InterviewerInnen persönlich gestellt und auch die Antworten von ihnen niedergeschrieben werden. Man würde mit hoher Wahrscheinlichkeit äußerst unterschiedliche Antworten erhalten. Genauso müßte man mit Verfälschungen rechnen, wenn Firmenchefs oder -chefinnen ihre Angestellten zur Zufriedenheit mit ihrer Arbeitssituation befragen.
Gütekriterien und andere Fehlerquellen erfordern, dass statistische Untersuchungen stets mit äußerster Sorgfalt durchgeführt werden: von der Erhebung der Daten bis zu deren Analyse, dass also die richtigen Methoden angewandt werden, deren Wahl auf der Eigenart der Daten und ihrer Verteilungen beruht und dass die Interpretation keineswegs über die Aussagekraft der Daten hinausgeht.
Verweise:
[1] &&& http://www.univie.ac.at/ksa/elearning/cp/ksamethoden/ksamethoden-76.html
2.4 Fehlerquellen bei statistischer Arbeit
Statistik ist der Versuch, aus einem Ausschnitt der Realität auf die Gesamtheit zu schließen. Dies bedeutet, dass unsere Aussagen über die (gesamte) Realität immer, ohne Ausnahme, mit einem Irrtumsrisiko behaftet sind, da wir nicht über vollständige Daten zur Grundgesamtheit[1] verfügen. Statistisch sprechen wir dabei von Fehlern der ersten und der zweiten Art.
Während Fehler der ersten und der zweiten Art zu nicht eliminarbaren Risiken der statistischen Arbeit gehören und auch bei sorgfältiger Herangehensweise nicht ausgeschlossen, sondern nur berücksichtigt werden können (siehe Irrtumswahrscheinlichkeit[2]), hängen individuell bedingte Fehler mit Mängeln bei der Datenaufnahme, -übertragung oder Analyse zusammen. Wir könnten diese unter fehler- bzw. mangelhafte Daten zusammenfassen.
Verweise:
[1] Siehe Kapitel 2.1
[2] Siehe Kapitel 1.3.2
2.4.1 Fehler erster und zweiter Art
Unter Fehler der ersten bzw. zweiten Art verstehen wir das systembedingte Problem, dass Hypothesen auch bei sorgfältigem Vorgehen fälschlich bestätigt oder verworfen werden.
Hypothesen am Beginn der Untersuchung
Bei Forschungsprojekten formulieren wir Hypothesen, deren Richtigkeit wir mit geeigneten Forschungs- und Analysemethoden untersuchen wollen. Eine derartige Ausgangshypothese oder Nullhypothese (in Kurzform oft auch H0 bezeichnet) könnte lauten: ’AfrikanerInnen werden am Arbeitsplatz weniger geschätzt als ChinesInnen.’.
Das Vorliegen einer Hypothese bedingt auch, dass es als Kontrast eine alternative Hypothese gibt (die wir bei der Erstellung des Konzepts als meist weniger wahrscheinlich einschätzen), die Alternativhypothese (in Kurzform oft auch H1 genannt). In unserem Fall könnte diese lauten: ’AfrikanerInnen werden am Arbeitsmarkt nicht weniger geschätzt als ChinesInnen.’.
Annahme oder Verwerfung von Hypothesen ist immer an Wahrscheinlichkeiten gebunden
Bei statistischen Analysen versuchen wir, Ergebnisse auf hohem Signifikanzniveau[1] zu erreichen. Wir sprechen davon, dass die gefundene Aussage mit einer Irrtumswahrscheinlichkeit von weniger als 5 %, weniger als 1 %, weniger als 1 ‰ zutrifft. Das bedeutet, dass unser Ergebnis, auf das wir so stolz sind, dennoch in 5 % aller Fälle, in 1 % aller Fälle etc. rein zufällig entstehen kann und, bei einer genügend häufigen Wiederholung, sogar muss.
Andererseits ist genauso denkbar, dass unser Ergebnis rein zufällig nicht den starken Zusammenhang zeigt, der normalerweise erscheint. Wir könnten auch bei großer Sorgfalt bei der Auswahl der Stichprobe überdurchschnittlich häufig auf Personen treffen, welche AfrikanerInnen besonders positiv gegenüber stehen.
Fehlerhafte Verwerfung bzw. Annahme von Hypothesen möglich
Es können also zwei verschiedene Fehler auftreten:
A. die Nullhypothese wird verworfen, obwohl sie richtig ist. Dies nennt man auch Fehler der ersten Art oder Alpha-Fehler;
B. die Nullhypothese wird angenommen, obwohl sie falsch ist. Dies bezeichnet man auch als Fehler der zweiten Art oder Beta-Fehler.
Mit der Zahl der statistischen Berechnungen steigt die Wahrscheinlichkeit von Fehlern der 1. oder 2. Art
Das Risiko, einem der beiden Fehler aufzusitzen, steigt natürlich mit der Höhe der Irrtumswahrscheinlichkeit sowie mit der Zahl der durchgeführten Analysen. Moderne PCs und Statistik-Software laden geradezu dazu ein, in kurzer Zeit tausende von Hypothesen zu überprüfen. Wenn wir 100 Variable miteinander kreuzen, erhalten wir (100x99)/2 Vergleiche, d.s. 4950 einzelne Untersuchungen auf signifikante Zusammenhänge. Wenn wir diese mit Chi-Quadrat-Tests auf dem 5 %-Irrtumsniveau untersuchen, erhalten wir im Normalfall 247,5 falsche Zusammenhänge (4950*0,05). Wir würden also in 247 Fällen einen Zusammenhang annehmen, obwohl er nicht vorhanden ist (Alpha-Fehler).
Kontrolle durch qualitative Überlegungen erforderlich
Derartige Massenvergleiche zeigen auch deutlich, dass statistische Berechnungen nicht losgelöst von qualitativen Überlegungen stattfinden dürfen. Bei statistischen Untersuchungen überraschend aufgetauchte Zusammenhänge müssen auch eine gewisse Stabilität und Systemkohärenz aufweisen, um akzeptiert werden zu können. D.h. sie müssen in einem gewissen Rahmen reproduzierbar sein und sie sollten nicht im Widerspruch zu offensichtlichen Fakten sein.
Verweise:
[1] Siehe Kapitel 1.3.2
2.4.2 Fehlerhafte oder mangelnde Daten
Fehler und Mängel können bei einer Reihe von Vorgängen bei statistisch unterstützten Forschungsprojekten erfolgen bzw. auftreten, wie z.B.:
A. Operationalisierungsfehler: bei der Operationalisierung[1] wurden verzerrende Messmethoden festgelegt;
B. Codierfehler: bei der Codierung[2] wurden, z.B. bei der Übertragung von Text-Daten in numerische Daten für interne Berechnungen von SPSS, Fehler begangen (z.B. die Vergabe des Zahlenwerts 4 in der Notenskala für ’Befriedigend’);
C. Interviewerfehler: bei der Datenaufnahme wurden fehlerhafte Werte eingetragen (z.B. eine Kinderzahl von 71 statt 7);
D. Widersprüchliche Datenlage: die Versuchspersonen oder die Datenquellen lieferten widersprüchliche Informationen, die sich in den Datenblättern wiederfinden;
E. Antwortverweigerung: verschiedene Fragen wurden von Versuchspersonen nicht beantwortet oder waren durch die Datenlage nicht erhebbar;
F. Eingabefehler: Datensätze wurden doppelt eingegeben;
G. Analysefehler: für die Analyse der Daten wurden die falschen Methoden[3] verwendet;
H. Interpretationsfehler: die Ergebnisse wurden richtig gerechnet, aber falsch interpretiert;
I. Grafiken[4] und Tabellen werden falsch oder ungenügend mit Zusatzinformationen versehen, was sowohl zu mangelndem Verständnis wie auch zu Nichtüberprüfbarkeit der Ergebnisse führen kann.
Verweise:
[1] Siehe Kapitel 2.2.1
[2] Siehe Kapitel 2.2.3.2
[3] Siehe Kapitel 3.1
[4] Siehe Kapitel 3.6.3
2.4.2.1 Eingabefehler
Meist werden Umfrageergebnisse zuerst handschriftlich aufgezeichnet. Danach werden die Daten in den PC übertragen, was mehrere potentielle Fehlerquellen berührt. Eine wenig leserliche Schrift kann zu Irrtümern bei der Eintragung in die Datenmatrix führen, genauso ’hängengebliebene Finger’ auf einer kleinen Tastatur, aber natürlich auch bewusste Falschangaben.
SPSS und Excel bieten verschiedene Möglichkeiten, die Eingabe von falschen Daten zu erschweren:
A. durch die Wahl geeigneter Datentypen
B. durch die Überprüfung, ob sich der eingetragene Wert innerhalb vorgegebener Grenzen befindet = Gültigkeitsprüfung.
2.4.2.1.1 Wahl geeigneter Datentypen mit SPSS
Verringerung des Risikos durch Wahl geeigneter Datentypen
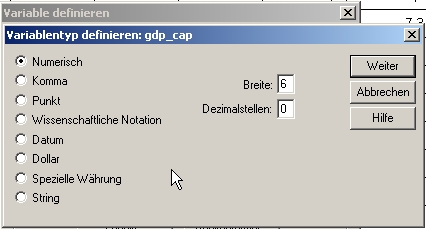
Besonders wichtig ist die richtige Definition des Datentyps (-> VARIABLENANSICHT - DATENTYP). In einem Stringfeld (oder Textfeld) können beliebige Zeichen stehen, in einem numerischen Feld nur Zahlen. Das bedeutet, dass durch Verschreiben keinerlei Buchstaben in ein numerisches Feld ’rutschen’ können. Der Datentyp kann jedoch noch wesentlich enger gefasst werden. Wenn ich im Feld Breite die Zahl 4 eintrage, kann ich z.B. bei numerischen Daten ausschließen, dass Jahreszahlen fehlerhaft durch Vertippen mit fünf Ziffern eingegeben werden. Gibt man bei Dezimalstellen 0 ein, sind nur ganze Zahlen möglich.
2.4.2.1.2 Gültigkeitsprüfung der Daten mit Excel
Unter Gültigkeitsprüfung von Daten versteht man die automatische Prüfung, ob aufgenommene Ausprägungen sich innerhalb eines vorgegebenen Bereichs befinden. Jeder außerhalb dieses Bereichs liegende Wert wird bei der Eingabe mit einer Fehlermeldung abgewiesen.
Für die meisten Variablen lassen sich mit geringer Sachkenntnis Ober- und Untergrenzen definieren, welche alle real auftretenden Ausprägungen umschließen. So könnte man bei der Aufnahme der Körpergröße von Erwachsenen eine Untergrenze von 80 cm und eine Obergrenze von 3 m annehmen; beim Lebensalter bei Erwachsenen eine Untergrenze von 18 und eine Obergrenze von 130; bei Schulnoten eine Untergrenze von 1 und eine Obergrenze von 5; beim Einkommen von Studierenden eine Untergrenze von 0 und eine Obergrenze von 4000 Euro.
Mit Excel geschieht dies folgendermaßen:
A. Man markiert die Spalte der Ausprägungen
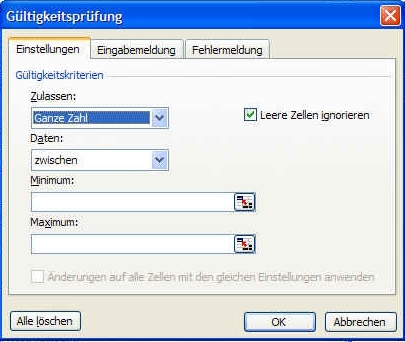
B. In der Menüleiste auf Daten und danach auf Gültigkeit klicken
C. Nun unter Zulassen Angabe des Datentyps machen. Wenn z.B. die Zahl der Kinder eingetragen werden sollte, würden wir hier Ganze Zahl wählen. Wählt man Liste aus, gelten alle Werte als gültig, welche sich in einer spezifischen Datei befinden (der Liste).
D. Unter Daten gibt man die Richtung der Ausprägungen an, also z.B. größer als, zwischen, ungleich etc. In unserem Fall der Kinderzahl wählen wir zwischen (auch größer oder gleich wäre denkbar).
E. Nun geben wir als Minimum-Wert ' die untere Begrenzung ein, in unserem Falle 0, da weniger Kinder nicht möglich sind und als Maximum in unserem Falle die Zahl 20 (kaum denkbar, dass jemand in Industrieländern eine höhere Kinderzahl aufweist).
F. Unter Eingabemeldung könnte man eine Meldung ausgeben lassen, welche bei Einträgen im Feld automatisch auf die Grenzen hinweist
G. Wichtiger ist es, unter Fehlermeldung anzugeben, warum ein eingetragener Wert als ungültig abgelehnt wird. Dazu wählen wir unter Typ eine bestimmte Signalform, in unserem Falle Warnung; danach geben wir unter Titel eine aussagekräftige Kurzmeldung und unter Fehlermeldung ausführlichere Erklärungen dazu ein.
Falls wir nun in Excel in der betreffenden Spalte für Kinderzahlen die Ausprägung 22 eingeben, erhalten wir folgende Warnmeldung:
2.4.2.2 Doppelte Datensätze
Mitunter kann es geschehen, dass der gleiche Datensatz fehlerhafterweise doppelt eingegeben wird.
Doppelt eingegebene Datensätze kann man in SPSS mit folgender Funktion finden:
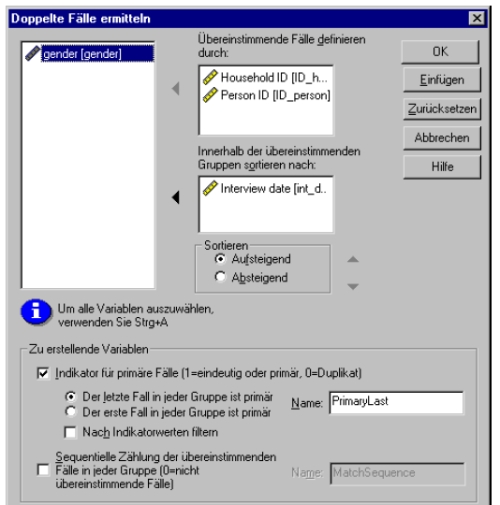
Klicken Sie auf DATEN - DOPPELTE FÄLLE ERMITTELN. Sie sehen folgendes Fenster:
Die wesentlichen Einträge hier sind:
A. Geben Sie unter Übereinstimmende Fälle definieren durch die Variablen an, welche zur Identifikation von Doppelgängern dienen. Das können normalerweise nur Variable sein, bei welchen Einträge eindeutig sein sollen (natürlich ist Eindeutigkeit auch durch eine Kombination mehrerer Variable erreichbar).
B. Sie können unter Innerhalb der übereinstimmenden Gruppen sortieren nach: noch eine Variable angeben, nach der sortiert werden soll.
Haben Sie somit doppelte Einträge gefunden, können Sie Fall für Fall entscheiden, wie Sie damit umgehen.
2.4.2.3 Fehlende Einträge
Was tun, wenn Einträge fehlen?
Nur bei den wenigsten Umfragen werden alle Fragen von allen Befragten beantwortet. Besonders tabuisierte Fragen wie vielleicht nach Bereichen der Sexualität, dem Einkommen, den politischen Neigungen werden oft nicht oder nur neutral beantwortet. Es stellt sich daher die Frage, ob und wie man die fehlenden Einträge interpretieren kann. Ein weiser Spruch der Kommunikationsforschung lautet: ’Man kann nicht nicht kommunizieren’ (Paul Watzlawick). Das bedeutet, dass vor allem bei tabusierten Fragen auch die Nichtbeantwortung von Fragen eine Information darstellt. Es könnte dementsprechend sein, dass bei manchen Fragen eine Nichtbeantwortung bedeutet: "Ich möchte nicht, dass man weiß, wie ich über diesen Bereich denke."
Beispiel: geringe Bekenntnisquote von FPÖ- WählerInnen
Viele Jahre lang hatten besonders FPÖ-WählerInnen während der Haider-Jahre große Angst, sich in Umfragen vor Wahlen zu ihrer Partei zu bekennen. Die Wahlergebnisse fielen daher für die FPÖ durch 1,5 Jahrzehnte stets wesentlich besser aus als die Umfrageergebnisse, was u.a. dazu führte, dass ihre Bekennerzahlen in Umfragen von den Meinungsforschungsinstituten einen substantiellen Zuschlag bekamen, um sich der tatsächlichen Unterstützung dieser Partei anzunähern.
Nichtbeantwortung auch durch Fehler möglich
In anderen, neutralen, Bereichen wird eine Nichtbeantwortung wieder eher als Übersehen oder als Ratlosigkeit (die Frage ist vielleicht unverständlich formuliert) gedeutet werden. Es gäbe kaum einen denkbaren Grund, die Frage nach seinem Lieblingsobst nicht zu beantworten.
Je nach Tabuisierungsgrad der Frage sind fehlende Einträge unterschiedlich aussagekräftig
Je nach Sachlage kann daher eine Nichtbeantwortung eine Art von Information oder einen Mangel darstellen. Im ersten Fall könnte es sein, dass z.B. besonders Personen, welche eine extrem abwehrende Haltung gegenüber MigrantInnen aufweisen (wie aus einer anderen Fragestellung erkennbar), besonders zur Nichtbeantwortung der Frage ’Welche Partei würden Sie wählen, wenn morgen Wahltag wäre?". Das heißt, dass wir uns bei auffallend häufiger Nichtbeantwortung von bestimmten Fragen die Frage stellen sollten, ob es bei den Nichtbeantwortenden gewisse Gemeinsamkeiten gibt und damit auch spezifische Motive der Nichtbeantwortung.
Wir müssen also bei der Behandlung der beiden Arten der Nichtbeantwortung differenzieren: im Falle der informationstragenden Nichtbeantwortung sollte der Antwort dennoch ein gewisser Wert beigemessen werden. Im Falle der informationsleeren Nichtbeantwortung sollten wir die Nichtantwort einfach aus der Gesamtzahl der möglichen Antworten ausschließen und dadurch die Stichprobengröße für diese Frage verkleinern.
2.4.2.3.1 Behandlung fehlender Daten mit SPSS
SPSS erlaubt, leere Felder automatisch mit bestimmten Einträgen auszufüllen oder dieselben in keinerlei Berechnungen einfließen zu lassen.
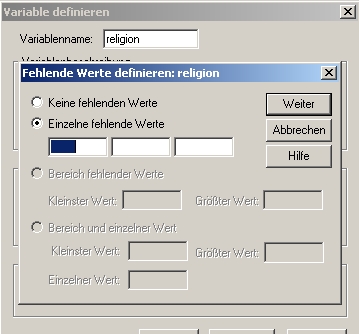
SPSS unterscheidet zwischen Systembedingt fehlenden Werten und Benutzerdefinierten fehlenden Werten. Werden z.B. Variable als numerisch definiert, werden leere Felder automatisch mit einem Komma in der Datenmatrix[1] markiert (Systembedingt). Bei Textfeldern muss ein fehlender Wert spezifisch deklariert werden (Benutzerdefinierter fehlender Wert):
Man kann hier genau definieren, was als fehlender Wert gelten soll. Soll ein leeres Feld als solcher gelten, drückt man im ersten Feld von Einzelne fehlende Werte einmal auf die Leertaste. Man erhält hier in einem Beispiel die folgende Ausgabe:
Man erkennt, dass in der vorletzten Zeile 2 fehlende Werte eingetragen wurden. Auch die Größe der tatsächlich berücksichtigten Stichprobe hat sich um 2 verringert (siehe drittletzte Zeile).
Falls man jedoch im Fenster Fehlende Werte definieren die Alternative Keine fehlenden Werte auswählt, erhalten Sie folgendes Ergebnis:
Die fehlenden Einträge in der vorletzten Zeile sind verschwunden, stattdessen findet sich in der ersten Zeile der ersten Spalte eine fehlende Beschreibung, neben der die Häufigkeit 2 steht. Die fehlenden Werte fließen hier voll in die Berechnung ein. Eine derartige leere Bezeichnung ist natürlich wenig anschaulich. Man muss sie daher für Bildschirm- und Printausgabe mit einer informativeren Beschreibung versehen. Dazu gehen wir wieder zur Variablenansicht und wählen in dieser (Variablen-)Labels aus.
In Wert fügen wir wieder eine Betätigung der Pausetaste ein, unter Wertelabel z.B. ’nicht beantwortet’. Leerfelder werden dadurch deutlich informativer dargestellt, s.u.:
Nun tauchen in der ersten Zeile die leeren Antworten mit einer klaren und verständlichen Beschreibung auf.
Verweise:
[1] Siehe Kapitel 2.2.3
3. Ausgewählte statistische Grundlagen und Analysemethoden
In den folgenden Abschnitten werden eine Reihe von Methoden der deskriptiven[1], teilweise auch der einfachen analytischen[2] Statistik sowie auch deren Anwendungsvoraussetzungen und Rahmenbedingungen vorgestellt.
Wir benötigen ausreichendes Wissen über die Art, Skalierung[3] und Verteilung[4] der Daten, um die dafür geeigneten statistischen Beschreibungs- und Analysemethoden wählen zu können. Dementsprechend wird dieses notwendige Hintergrundwissen intensiver diskutiert. Danach werden grundlegende deskriptive und analytische statistische Methoden dargestellt, wobei der Schwerpunkt auf ersteren liegt. Abschließend wird auf die grafische Darbietung der Ergebnisse in Form von Diagrammen eingegangen.
Verweise:
[1] Siehe Kapitel 1.2.1
[2] Siehe Kapitel 1.2.2
[3] Siehe Kapitel 3.1.2
[4] Siehe Kapitel 3.1.3
3.1 Notwendiges Wissen für die Wahl geeigneter statistischer Analysemethoden
Analysemethoden sind abhängig von Datenart, -ausprägung, -anzahl und -verteilung:
Die Statistik bietet eine Vielzahl von Verfahren, mit deren Hilfe man Aufschlüsse über Sachverhalte gewinnen kann. Die meisten Verfahren können jedoch nur verwendet werden, wenn bestimmte Bedingungen erfüllt sind. Die Auswahl der möglichen Verfahren hängt besonders ab von
- der Art der Daten und den damit zusammenhängenden Skalenniveaus[1]
- der Verteilung[2] der Ausprägungen einer Variable
- der Größe der Stichprobe[3]
- dem (Nicht-)Auftreten von sogenannten ’Ausreißern’ oder Extremdaten
Falls Verfahren außerhalb ihrer Anwendungsbedingungen verwendet werden, ist die Wahrscheinlichkeit groß, dass sinnleere oder falsche Aussagen erhalten werden.
Körpergrößen und Lieblingsobst
Wenn wir in einer Schulklasse die durchschnittliche Körpergröße der SchülerInnen ermitteln wollen, wäre das arithmetische Mittel[4] eine durchaus vernünftige Kennzahl. Wir zählen dazu alle Körpergrößen zusammen und dividieren die Summe durch die Anzahl der KlassenschülerInnen. Wenn wir hingegen ermitteln möchten, was diese Schulklasse als Lieblingsobst bevorzugt, wäre das arithmetische Mittel Schwachsinn. Wir kämen dann zu wenig sinnvollen Aussagen, dass die Klasse 0,17 Äpfel, 0,12 Orangen, 0,11 Bananen etc. als Lieblingsobst aufweist.
Dass im ersten Fall das arithmetische Mittel verwendet werden konnte, im zweiten Falle jedoch nicht, hängt mit den unterschiedlichen Skalenniveaus zusammen. So gehört die Körpergröße zur Proportionalskala[5], während das Lieblingsobst in eine Nominalskala[6] eingeordnet wird.
Verweise:
[1] Siehe Kapitel 3.1.2
[2] Siehe Kapitel 3.1.3
[3] Siehe Kapitel 2.1.1
[4] Siehe Kapitel 3.3.2
[5] Siehe Kapitel 3.1.2.5
[6] Siehe Kapitel 3.1.2.2
3.1.1 Arten von Messwerten (Daten)
Statistisch unterscheidet man Daten
- in welcher Weise die Umsetzung in numerische Werte zur sinnvollen Ordnung und weiteren möglichen Erkenntnissen führt: metrische und nichtmetrische Variable;
- über die Abstufungen ihrer Ausprägungen: stetige und diskrete Variable
3.1.1.1 Metrische und nichtmetrische Variablen
Metrische und nichtmetrische Variablen
Prinzipiell können wir zwischen metrischen und nichtmetrischen Variablen unterscheiden. Als metrische Merkmale (auch quantitative genannt) bezeichnet man Merkmale, deren Ausprägungen sich mittels Zahlen darstellen lassen, wobei auch Rangunterschiede und Abstand sinnvoll interpretiert werden können. Als nichtmetrische Variablen werden dementsprechend alle anderen bezeichnet.
Beispiele:
Wir können somit z.B. Körpergrößen sinnvoll reihen (von klein nach groß mit beliebig feinen Abstufungen) und auch Größenunterschiede vernünftig interpretieren. Fragen wir hingegen nach dem Lieblingsobst, wird die Reihung der Ergebnisse willkürlich sein und meist alphabetisch erfolgen. Theoretisch könnte man jedem Obst einen Zahlenwert zuweisen, dieser wird jedoch nichts über den dahinterliegenden Wert aussagen, also zufällig mit diesem verbunden sein. Ränge, wie z.B. der Beliebteste, der Zweitbeliebteste, der Drittbeliebteste usw. lassen sich zwar sinnvoll reihen, ihre Abstände lassen sich aber nicht interpretieren. D.h. wir können nicht sagen, dass der Drittbeliebteste gegenüber dem Viertbeliebtesten den gleichen Abstand hat wie der Beliebteste gegenüber dem Zweitbeliebtesten. Daher sind sowohl Nominaldaten (wie das erwähnte Obst) wie auch Ordinaldaten nichtmetrisch.
3.1.1.2 Stetige und diskrete Variablen
Stetige und diskrete Variablen
Metrische Daten können ebenfalls wieder unterschieden werden, nämlich in
- stetige oder kontinuierliche, wenn sie jeden beliebigen Wert eines bestimmten Intervalls annehmen können (z.B. Körpergröße 175,33 cm, Temperatur); und
- diskrete, wenn sie nur endlich viele Werte annehmen können (z.B. Augenzahl beim Würfeln, Anzahl der Kinder)
3.1.2 Skalenniveaus
Skalenniveaus (von scala ital. ’Treppe’) sind eindimensionale Folgen von Positionen, die unterschiedliche Ausprägungen eines Merkmals anzeigen.
Jede Variable kann einer bestimmten Form von Skalierung zugeordnet werden. Nach der Möglichkeit, die Ausprägungen sinnvoll zu reihen und bestimmte mathematische Operationen durchzuführen, unterscheidet man zwischen vier verschiedenen Skalierungsniveaus: Nominalskalierung, Ordinalskalierung, Intervallskalierung und Proportionalskalierung.
Je nach Skalierungsniveau können sehr viele Analyseverfahren (wie bei der Proportionalskalierung) oder sehr wenige Verfahren (wie bei der Nominalskalierung) zur Auswertung eingesetzt werden. Daher ist die Wahl der Art der Daten und Skalenniveaus bereits bei der Forschungskonzeption zu berücksichtigen.
3.1.2.1 Skalierungsniveaus bildlich erklärt
Die technische Definition der Skalierungsniveaus hat den Nachteil, dass viele Menschen sich unter ihnen nichts vorstellen können. Machen wir es etwas anschaulicher und auch mit Treppen.
Stellen Sie sich vor, Tischler sehr unterschiedlicher Begabung und Erfahrung würden Stufen für eine Treppe bauen.
Nominalskala:
Wir hätten zuerst den Amateurtischler, welcher extrem ungleichförmige Stufen baut. Die eine Stufe ist links viel höher als rechts, die andere hinten höher als vorne. Keine einzige ist so gleichförmig, dass sie überall höher ist als alle anderen, keine einzige ist so gleichförmig, dass sie überall niedriger ist als alle anderen. Mit anderen Worten: wir können die Stufen beliebig hintereinander reihen. Wir finden keinen eindeutigen logischen und zwingenden Ansatz zur Reihung. Nehmen wir die Höhe links, würden wir die Stufe A vor der Stufe B vor der Stufe C reihen; nehmen wir die Höhe rechts, die Stufe B vor der Stufe C vor der Stufe A; nehmen wir die Höhe vorne etc.
Eine derartige Treppe, die sich beliebig zusammensetzen lässt und eigentlich gar keine Treppe ist, weil man auf ihr nicht höher steigen kann, würde der Nominalskala entsprechen: Was besitzt man: Äpfel, Birnen, ein Auto, einen Hund etc.
Ordinalskala:
Der Tischler wird nun etwas geschickter. Er schafft es, die Stufen jeweils unterschiedlich hoch zu machen und zwar überall. Die Stufe B ist 1,2x so hoch wie die Stufe A, die Stufe C doppelt so hoch wie die Stufe B, die Stufe D 3x so hoch wie die Stufe C, die Stufe E 1,3x so hoch wie die Stufe D. Es ist nicht vorauszusagen, um wieviel die nächsthöhere Stufe höher sein wird, aber man weiß, sie ist höher. Es ist ein beschwerlicher Aufstieg, aber es ist ein Aufstieg. Das würde einer Ordinalskala entsprechen. Ein Beispiel dafür wäre eine Notenskala. Man weiß zwar nicht, um wieviel besser ein Schüler mit einem Sehr Gut als ein Schüler mit einem Gut war, aber dass es einen Unterschied gegeben hat, erscheint klar zu sein (außer der Lehrer war bekannt subjektiv, was vorkommen soll).
Intervallskala:
Der Tischler wird noch geschickter. er schafft es sogar alle Stufen jeweils um 30 cm höher zu machen als die jeweils vorausgegangene. Man kann nun blind die Stufen hinaufgehen, weil man die Abstände kennt. Das Problem: Die Stiege steht auf einem Schiff, welches im Mittelmeer herumfährt. Ich weiss nun zwar, dass ich 30 cm höher steige, wenn ich eine Stufe hinaufschreite und 90, wenn ich drei Stufen hinaufschreite, aber ich kann nicht angeben, in welcher Höhe über dem Meeresboden ich mich befinde. Sind es 150 m, sind es 300? Dadurch kann ich auch nicht angeben, ob ich mich auf der übernächsten Stufe doppelt so hoch befinde wie jetzt. Ich kann zwar mit fixen Abständen rechnen, aber ich habe keinen absoluten Nullpunkt (wo es nicht mehr tiefer geht, wie zum Meeresboden) zum Vergleich und daher kann ich nicht angeben, um wieviel höher ich sein werde, wenn ich x Stufen höhersteige. Dies nennt man eine Intervallskala, die Stufen werden in gleichen Intervallen höher.
Ein Beispiel dafür wäre unsere Temperaturskala in Celsius, wo wir nicht vom absoluten Nullpunkt ausgehen (das wäre der Meeresboden oder - 273 Grad Celsius), sondern von einem willkürlichen (nämlich vom Schiffsboden aus oder 0 Grad). Daher ist die Aussage, 10 Grad ist 5 Grad wärmer als 5 Grad richtig, aber die Aussage falsch, dass es damit doppelt so warm ist, denn tatsächlich hätte ich ein Verhältnis von 283 Grad: 278 Grad (vom absoluten Nullpunkt aus gemessen).
Proportionalskala:
Wenn wir die gleiche Stiege wie bei der Intervallskala nun an Land bringen und sie auf festen Boden stellen, dann können wir von einer Proportionalskala sprechen. Endlich können wir, wenn wir uns auf der dritten Stufe befinden, nicht nur sagen, wir sind jetzt 60 cm höher als auf der ersten. Wir können auch endlich die Verhältnisse richtig interpretieren. Wir können nun auch korrekt angeben, dass wir uns jetzt auf der dritten Stufe dreimal so hoch wie auf der ersten Stufe befinden (mit dem festen Boden als absolutem Nullpunkt, unter den kein Abstieg möglich ist). Dies ist nun eine Proportionalskala. Ein Beispiel dafür wären Körpergrößen. Jemand, der 1,80 m groß ist, ist doppelt so groß wie jemand, der 90 cm groß ist.
3.1.2.2 Nominalskalierung
Bei der Nominalskalierung handelt es sich um eine Klassifizierung von Objekten, bei welcher keinerlei sinnvolle Rangreihung möglich ist, weshalb meist zur alphabetischen Reihung gegriffen wird. Größer und kleiner, mehr oder weniger wichtig, mehr oder weniger ausgeprägt kann nicht unterschieden werden. Jede Reihung ist gleich sinnvoll.
Beispiele für Nominalskalierungen wären Zeitungen, die man liest; das Obst, das man isst; das Geschlecht von ProbandInnen; die Farben von Kleidungsstücken etc.
3.1.2.3 Ordinalskalierung
Bei der Ordinal- oder Rangskalierung werden Gegenstände oder Sachverhalte miteinander verglichen und nur der Größe oder Intensität entsprechend gereiht. Eine Rangreihung ist möglich und sinnvoll, jedoch können die Abstände nicht interpretiert werden, d.h. der Abstand vom Zweit- zum Drittgrößten kann anders sein als vom Dritt- zum Viertgrößten.
Beispiele wären die Beliebtheit von SchülerInnen (hier kann ich diese eindeutig danach reihen), die Sympathie für Zuwanderer etc.
Schulnoten ordinal- oder intervallskaliert?
Schulnoten werden von vielen behandelt, wie wenn sie zur Intervallskalierung gehören würden, in welcher Abstände interpretiert werden können. Daher errechnen viele zur Beurteilung der Qualität einer Klasse das arithmetische Mittel von Noten, was man jedoch nur bei zumindest intervallskalierten Variablen machen sollte. Überlegen wir: Falls Schulnoten intervallskaliert wären, müsste der Abstand von einer Schulnote zur nächstbesseren/- schlechteren einem präzisen und stabilen Leistungsunterschied zwischen SchülerInnen entsprechen. Oft ’steht’ man jedoch zwischen zwei Noten, die PrüferIn muss sich dennoch für eine entscheiden. Auch wenn alle SchülerInnen einer extrem begabten Klasse eine sehr gute Arbeit abgeben, wird die PrüferIn dennoch meistens versuchen, zwischen ihnen durch unterschiedliche Noten zu differenzieren, um die Motivation und den anspornenden Wettbewerb hochzuhalten. Daher gibt es trotz des offiziellen objektiven Anspruchs von Schulnoten einen zu hohen subjektiven Einfluss, um sie als intervallskalierte Variablen behandeln zu können.
3.1.2.4 Intervallskalierung
Bei der Intervallskalierung nimmt man gleiche Abstände (Intervalle) zwischen benachbarten Ausprägungen an, aber einen nur relativen und keinen absoluten Nullpunkt. Es kann zwar der Abstand zwischen den Werten interpretiert werden, nicht aber das Verhältnis der Werte zueinander.
Ein Beispiel für eine Intervallskala ist z.B. die Temperatur in Celsius. Es wäre falsch, anzunehmen, dass 10 Grad doppelt so warm sind wie 5 Grad. Bezogen auf den absoluten Nullpunkt (- 273 Grad) wäre das Verhältnis zwischen 10 Grad und 5 Grad genau 268:263.
3.1.2.5 Proportionalskalierung
Bei der Verhältnis- oder Proportionalskalierung gibt es einen absoluten Nullpunkt. Sowohl der Abstand zweier Werte wie auch ihr Verhältnis zueinander können interpretiert werden. Ein Baum mit einer Höhe von 3,6 Metern ist doppelt so hoch wie ein Baum mit einer Höhe von 1,8 Metern.
Beispiele für diese Form der Skalierung wären z.B. Körpergrößen, der Vitamingehalt von Früchten; der Wassergehalt von Körpern oder die Entfernung von Orten.
3.1.2.6 Skalierungstypen, Aussagen und Methoden
Die unterschiedlichen Skalierungsformen lassen unterschiedliche Analysemethoden zu:
Metrische Merkmale[1] finden sich bei Intervall- und Proportionalskalierung, nichtmetrische bei Nominal- und Ordinalskalierung.
Verweise:
[1] Siehe Kapitel 3.1.1.1
3.1.3 Verteilungen
(Häufigkeits-)Verteilungen geben Aufschluss über die Häufung aller Ausprägungen von Variablen. Man kann prinzipiell zwischen monovariablen und bivariablen Verteilungen unterscheiden.
Monovariable Verteilungen zeigen die Verteilung einer einzigen Variable, bei bivariablen Verteilungen werden die Häufigkeiten der einander entsprechenden Ausprägungen zweier Variablen aufgezählt, also z.B. 16 Personen sind sowohl weiblich wie auch Raucherinnen, 13 Personen männnlich und Nichtraucher.
Verteilungen können sowohl tabellarisch wie auch grafisch in Form von Diagrammen[1] dargestellt werden.
Zur tabellarischen Darstellung gelangt man, indem man die Werte (nach Möglichkeit sinnvoll) reiht und daneben die jeweilige Häufigkeit der Werte einträgt.
Zur grafischen Form gelangt man, wenn man in einem Diagramm auf der x- Achse die Ausprägung von Werten einträgt (z.B. die Körpergröße einer Person x) und auf der y- Achse deren Häufigkeit (= Zahl der Personen, welche genau diese Körpergröße aufweisen), dann können wir die Schnittpunkte mit Linien verbinden, wodurch sich eine Verteilungskurve ergibt. Die Standard- Darstellungsform dafür ist das Streudiagramm[2].
Verschiedene Verfahren erforden eine vorliegende Normalverteilung, die mit verschiedenen Prozeduren abschätzbar ist.
Verweise:
[1] Siehe Kapitel 3.6
[2] Siehe Kapitel 3.6.1.6
3.1.3.1 Normalverteilung
Von einer Normalverteilung sprechen wir, wenn
- die größte Häufigkeit in der Nähe des arithmetischen Mittel[1] auftritt und somit das arithmetische Mittel annähernd mit dem Median[2] und mit dem Modalwert[3] zusammenfällt;
- die Häufigkeiten[4] der Werte umso mehr abnehmen, je weiter sie sich vom Mittelwert entfernen;
- wenn sowohl links wie rechts des Mittelwerts eine prinzipielle Symmetrie vorliegt;
- wenn die Verteilungskurve glockenförmig ist.
Eine Normalverteilung sieht wie in der folgenden Grafik aus:
Die im Diagramm verlaufende Kurve gibt die Häufigkeit der jeweiligen Werte an. Man sieht, dass die größten Häufigkeiten beim Mittelwert auftreten (0), die geringsten Häufigkeiten an den Extremen, wobei die Kurve glockenförmig verläuft (so genannte Gauß’sche Glockenkurve).
Dies wäre eine optimale Normalverteilung.
Verweise:
[1] Siehe Kapitel 3.3.2
[2] Siehe Kapitel 3.3.3
[3] Siehe Kapitel 3.3.1
[4] Siehe Kapitel 3.1.3.3.2
3.1.3.2 Andere Verteilungsformen
Neben der Normalverteilung können viele andere Verteilungsformen auftreten.
Oft sind die Verteilungen schief, man unterscheidet dann zwischen linksschiefen oder rechtsschiefen Verteilungen.
Bei der linksschiefen Verteilung (negative skew) liegt der höchste Punkt der Verteilung rechts (d.h. hier befindet sich der Großteil der Einträge), während nach links ein langgezogener Abfall eintritt (d.h. es treten dort selten verwendete Extremwerte auf). In linksschiefen Verteilungen ist der Median[1] größer als das arithmetische Mittel[2].
Bei der rechtsschiefen Verteilung (positive skew) finden wir die überwiegende Mehrzahl der Einträge auf der linken Seite und damit auch den höchsten Punkt der Kurve, während nach rechts wenige Einträge auftauchen. Typisch für eine derartige Verteilung ist die Einkommensverteilung sozial ungerechter Länder, in welchen wenigen MultimilliardärInneen viele KleinverdienerInnen gegenüberstehen. In rechtsschiefen Verteilungen ist der Median kleiner als das arithmetische Mittel.
Verteilungen können auch mehrere Gipfel aufweisen:
Diese Verteilung weist insgesamt zwei Gipfel auf. Sie wird als bimodal (zweigipfelig) bezeichnet.
Diese Verteilung ist rechteckig. Sie könnte bei einer kleinen Stichprobe[3] auftreten, wenn fast alle Werte die gleiche Häufigkeit[4] aufweisen.
Diese Verteilungsform ist u-förmig. Die Extremwerte kommen sehr häufig vor, während mittlere Ausprägungen fast nicht auftreten. Auch diese Verteilung ist bimodal.
Verweise:
[1] Siehe Kapitel 3.3.3
[2] Siehe Kapitel 3.3.2
[3] Siehe Kapitel 2.1.1
[4] Siehe Kapitel 3.1.3.3.2
3.1.3.3 Test auf Normalverteilung
Verschiedene Verfahren sind nur sinnvoll anwendbar, falls annähernd eine Normalverteilung der Daten vorliegt. Dazu gehört z.B. die Maßkorrelation[1], aber auch das arithmetische Mittel[2] ist nur wenig aussagekräftig, wenn die Verteilung[3] der Daten durch Ausreißer und extreme Schiefe geprägt sind.
Für den Nachweis einer Normalverteilung kann auf drei wesentliche Methoden zurückgegriffen werden:
- optisch: Für die optische Abschätzung der Normalverteilung kann auf die grafische Wiedergabe (siehe oben, mit Statistik- Programmen z.B. mit der grafischen Darstellung des Histogramms[4]) zurückgegriffen werden
- statistisch-mathematisch auf den Kolmogorov-Smirnov-Test (falls die Werte nicht in Klassen eingeteilt sind, besonders auch bei kleinen Stichproben)
- oder auf den Chi-Quadrat-Test (Wikipedia)[5] (bei in Klassen eingeteilten Daten)
Erkennung mit SPSS
Diese verschiedenen und als eigene Unterpunkte angeführten Untersuchungen können unter SPSS auch gleichzeitig getätigt werden. Klicken Sie dazu auf ANALYSIEREN -> DESKRIPTIVE STATISTIKEN -> EXPLORATIVE DATENANALYSE. Wählen Sie dort unter ’Anzeige’ die Alternative ’Beide’ und unter ’Diagramm’ die Alternative ’Normalverteilungsdiagramm mit Tests’. Dann wird in der Bildschirmausgabe der Resultate ein eigener Punkt aufgeführt: ’Tests auf Normalverteilung’, von denen uns besonders der erste der beiden Tests interessiert ’Kolmogorov-Smirnov’ (eigentlich eine verschärfte Variante dieses Tests). Liegt der Wert, welcher unter ’Signifikanz steht’, unter 0,05, so ist mit 95 % Sicherheit eine Normalverteilung zu verwerfen, liegt er unter 0,01, sogar mit 99 % Sicherheit.
Verweise:
[1] Siehe Kapitel 3.5.3.1
[2] Siehe Kapitel 3.3.2
[3] Siehe Kapitel 3.1.3
[4] Siehe Kapitel 3.6.1.5
[5] http://de.wikipedia.org/wiki/Chi-Quadrat-Test
3.1.3.3.1 Optischer Nachweis einer Normalverteilung: das Histogramm
Das Histogramm[1] liefert uns einen ersten und recht brauchbaren Eindruck, ob die von uns analysierten Daten weitgehend normalverteilt sind. Mit SPSS ist die Herstellung eines derartigen Diagramms ein Kinderspiel:
A. Klicken Sie in der Menüleiste auf GRAFIKEN
B. Wählen Sie Histogramm
C. Wählen Sie die zu untersuchende Variable aus
D. Lassen Sie sich am besten auch die Normalverteilungskurve zu Vergleichszwecken hinzeichnen (mit Häkchen markieren).
E. Klicken Sie auf OK
Dann erhalten Sie z.B. das folgende Histogramm (alle folgenden Histogramme und Analysen wurden von der SPSS-Datei world95.sav abgeleitet):
Hier ist z.B. eine stärkere Abweichung von der Normalverteilung gegeben. Man beachte den großen Zwischenraum zwischen der Normalverteilungskurve und den tatsächlichen Werten bei einem Kalorien-Input von etwa 3000. Dennoch wäre auf dem 5-%-Signifikanz-Niveau die Annahme einer Normalverteilung mit dem Kolmogorov-Smirnov-Test[2] noch nicht widerlegt (wohl aber auf dem 10-%-Niveau).
Das folgende Diagramm zeigt eine noch deutlich stärkere Abweichung von der Normalverteilung:
In diesem Fall ist auch der Kolmogorov-Smirnov-Test hochgradig signifikant (sowohl auf dem 5-% wie auch auf dem 1-%-Niveau), weshalb die Annahme einer Normalverteilung verworfen werden muss.
Deutlich normalverteilt, sowohl grafisch erkennbar wie auch mit dem Kolmogorov-Smirnov-Test nicht verwerfbar, ist die folgende Verteilung. Es finden sich kaum Zwischenräume zwischen der Normalverteilungskurve und der tatsächlichen Verteilung:
Man sieht, dass das Histogramm meist eine sehr gute Abschätzmöglichkeit erlaubt, ob Variable normalverteilt sind.
Verweise:
[1] Siehe Kapitel 3.6.1.5
[2] Siehe Kapitel 3.1.3.3.2
3.1.3.3.2 Nachweis der Normalverteilung: Kolmogorov-Smirnov-Test
Der Kolmogorov-Smirnov-Test kann auch bei kleineren Stichproben eingesetzt werden, um zu überprüfen, ob eine gegebene Verteilung mit hoher Wahrscheinlichkeit von der Normalverteilung abweicht.
Die Berechnung basiert auf dem Vergleich mit einer hypothetischen Normalverteilungskurve (Bild von Internet-Enzyklopädie Wikipedia: http://de.wikipedia.org/wiki/Kolmogorow-Smirnow-Test[1]):
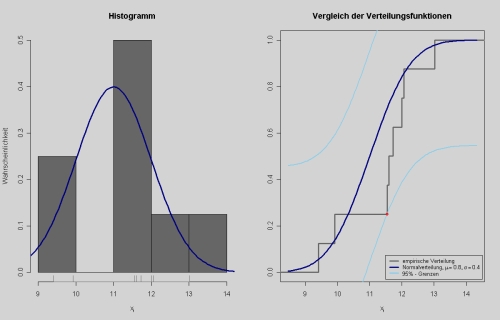
Die Logik der Berechnung geht davon aus, dass die tatsächliche Verteilung von einer hypothetischen Normalverteilung an einem beliebigen Punkt eine bestimmte flächenmäßige Abweichung nicht überschreiten darf, andernfalls müsste die Annahme einer Normalverteilung verworfen werden. Daher wird in einer Reihe von Rechenschritten die jeweilige konkrete Abweichung errechnet. Die größte auftretende Abweichung wird mit einer Tafel des Kolmogorov- Smirnov-Tests verglichen.
Ein Beispiel einer manuellen Berechnung kann hier eingesehen werden. Natürlich werden die Werte heute wesentlich komfortabler, z.B. mit SPSS, ermittelt.
Verweise:
[1] http://de.wikipedia.org/wiki/Kolmogorow-Smirnow-Test
3.1.3.3.2.1 Kolmogorov-Smirnov-Test mit SPSS
A. Sie wählen in SPSS den Menüpunkt ANALYSIEREN
B. Aus den heruntergeklappten Alternativen wählen Sie NICHTPARAMETRISCHE TESTS
C. Aus den nächsten Auswahlpunkten, die sich rechts öffnen, wählen Sie K-S BEI EINER STICHPROBE....
D. Nun wählen Sie die Testvariable aus, welche Sie auf Normalverteilung prüfen möchten. Achten Sie darauf, dass links unten unter Testverteilung der Punkt Normal angewählt ist.
E. Klicken Sie auf OK
F. Sie erhalten nun eine Bildschirmausgabe wie folgende:
G. Hier sind für uns die folgenden Werte von Belang: 1. N (in diesem Falle 8), Extremste Differenzen 0,320) und Asymptotische Signifikanz.
H. Nun vergleichen wir diese beiden ersten Werte mit einer Tabelle für den Kolmogorov-Smirnov-Test. Die nachfolgende Tabelle gibt bei einer 5 % Irrtumswahrscheinlichkeit Grenzwerte für Stichproben an, bei denen n zwischen 1-35 liegt.
Wir suchen nun den Wert für N = 8 und sehen dort die Zahl 0,454. Falls die Extremste Differenz in unserem Rechenbeispiel diesen Wert überschreitet, liegt mit 95 % Wahrscheinlichkeit keine Normalverteilung vor. In unserem Fall haben wir jedoch eine Extremste Differenz von nur 0,32. Das Ergebnis wird am Besten so interpretiert, dass die theoretische Annahme einer Standardverteilung nicht verworfen werden muss. Ein wirklicher Beweis für eine Standard- Verteilung liegt allerdings dadurch nicht vor.
Auch unser Wert für die Asymptotische Signifikanz ist weit größer als der Grenzwert 0,05. Dieser würde besagen, dass nur in 5 % aller Fälle eine derartige Verteilung wirklich normalverteilt ist. Ein Wert von 0,02 wäre hingegen deutlich kleiner, daher würde die Annahme einer Normalverteilung verworfen werden (auf dem 5 % Signifikanzniveau[1]). Da unser Wert jedoch deutlich darüber liegt, kann die Arbeitshypothese einer Normalverteilung auf diesem Signifikanzniveau nicht verworfen werden.
Achtung: Der Kolmogorov-Smirnov-Test benötigt, v.a. bei kleinen Stichproben, extreme Abweichungen von einer Normalverteilung, um auf höheren Signifikanzniveaus die Annahme einer Normalverteilung zu verwerfen. Daher ist eine Nichtverwerfung der Annahme einer Normalverteilung durch diese Berechnungsform noch kein Beweis für das Vorliegen einer Normalverteilung. Sollte sich im Histogramm[2] eine extreme Abweichung von der fakultativ gezogenen Normalverteilungskurve zeigen, dann sollte man, auch wenn der Kolmogorov-Smirnov-Test diese nicht verwirft, dennoch eher zu nicht parametrischen Tests greifen (wie z.B. dem T-Test etc.)
Hier ein Link zu weiterführenden Tabellen, in welchen noch weitere Irrtumswahrscheinlichkeiten für die Berechnung der Abweichung von einer Standardverteilung herangezogen werden: https://www.erieri.com/dlc[3]
Verweise:
[1] Siehe Kapitel 1.3.2
[2] Siehe Kapitel 3.6.1.5
[3] https://www.erieri.com/dlc/onlinetextbook/table7
3.2 Die Ermittlung von Häufigkeiten
Bei der Ermittlung von Häufigkeiten stellen wir fest, wie oft die verschiedenen Messwerte auftreten.
Die Ermittlung von Häufigkeiten ist das einfachste statistische Verfahren und kann für jede Art von Skala[1] angewandt werden. Die Häufigkeiten der Messwerte geben uns Hinweise auf ihre Verteilung[2] d.h. wie oft die einzelnen Ausprägungen vorkamen. Die Kenntnis dieser Verteilung gibt uns somit Auskunft darüber, was in einer untersuchten Stichprobe der Normalfall, und was die Ausnahme ist.
Dabei wird das Auftreten von Werten gezählt. Prinzipiell unterscheiden wir zwischen
- Monovariablen Verteilungen: eine einzige Variable wird gezählt. So kommen wir z.B. zu Häufigkeiten von Schulnoten (22 SchülerInnen hatten eine 1, 37 eine 2 usw.)
- Bi- bzw. multivariablen Verteilungen: Es wird gezählt, wie häufig Kombinationen von zwei oder mehr Variablen auftreten (z.B. Schulnoten und soziale Schicht; 17 SchülerInnen gehörten zur Oberschicht und hatten eine 1, 22 SchülerInnen zur Oberschicht und hatten eine 2 etc.). Mit Bi- oder multivariablen Verteilungen möchte man Zusammenhänge zwischen zwei Variablen feststellen.
Die tabellarische Darstellung der Häufigkeiten in bi- bzw. multivariablen Verteilungen wird auch als Kreuztabelle[3] oder Kontingenztafel bezeichnet.
Nach der Systematik der Darstellung unterscheidet man zwischen der Urliste, der primären Tafel bzw. der Häufigkeitstabelle.
Verweise:
[1] Siehe Kapitel 3.1.2
[2] Siehe Kapitel 3.1.3
[3] Siehe Kapitel 3.5.2
3.2.1 Liste und Tafeln
Urliste
Aufgenommene Messwerte sind anfangs ungeordnet. Denken Sie z.B. an 30 Personen, deren Alter Sie abgefragt haben, ohne die Einträge größenmäßig zu ordnen. Diese ungeordnete Liste wird als so genannte Urliste bezeichnet. Eine Urliste ist die ungeordnete Aufzählung der Werte in der gleichen Reihenfolge, in der sie während der Abfrage aufgenommen wurden.
Beispiel: Kinderzahl von Befragten
Primäre Tafel
Wesentlich übersichtlicher ist bereits die primäre Tafel, in welcher die Ausprägungen sortiert werden. Sie gibt deutlich mehr Aufschluss über die Charakteristiken der Daten. Hier ist auf einen Blick erkennbar, dass die Messwerte 1 und 2 am häufigsten vorkommen:
Dennoch ist auch eine Primäre Tafel im Vergleich mit einer Häufigkeitstabelle wenig übersichtlich.
3.2.2 Häufigkeitstabelle
Häufigkeitstabellen zeigen in tabellarischer Form die Ausprägungen einer Variablen verbunden mit deren Häufigkeit. Sie sind weit übersichtlicher als Listen und Tafeln.
Dabei trägt man in der 1. Spalte die Messwerte ein (wie z.B. Kinderzahl oder hier Ländernamen), in der 2. Spalte die absolute Häufigkeit der Messwerte (durchzählen, wie oft z.B. Frankreich genannt wird) und in Spalte 3 berechnet man die relative Häufigkeit. Die relative Häufigkeit errechnet man folgendermaßen: man nimmt die absolute Häufigkeit eines Messwertes (z.B. waren 16 FranzösInnen beim Kongress), dividiert diesen durch die Summe der Messwerte (hier insgesamt 50 anwesende WissenschaftlerInnen) und multipliziert das Ergebnis mit 10 (um auf Prozentwerte zu kommen). Für FranzösInnen daher 16/50*100=32 %.Akkumulierte Häufigkeit
Wenn keine Nominalskalierung[1] vorliegt, ist auch die Darstellung der akkumulierten Häufigkeit sinnvoll. Sie gibt Auskunft über die Häufigkeit aller Messwerte, die bis zu einem bestimmten Niveau auftreten.
Man errechnet sie folgendermaßen: Man zählt alle relativen Häufigkeiten zusammen, die einschließlich dieser Zeile auftraten: Die akkumulierte Häufigkeit für die Note 3 (= alle EthnologInnen, die zumindest die Note 3 erhielten) wäre daher: 19,2 % + 21,8 % + 28,2 % = 69,2 %.
Eine derartige Häufigkeitstabelle kann, wie vorhin beschrieben, auch mehrdimensional sein (multivariabel):Eine Häufigkeitstabelle hat folgende Vorzüge:
- Sie ist übersichtlicher als eine Urliste
- Sie ist kürzer als eine primäre Tafel
- Sie ist ökonomisch
- Sie erlaubt eine leichte Beurteilung der Verteilung
- Trotz dieser Vorteile tritt kein Informationsverlust auf.
Verweise:
[1] Siehe Kapitel 3.1.2.2
3.2.2.1 Häufigkeitsberechnung mit SPSS
Die Berechnung von Häufigkeiten mit SPSS erfolgt folgendermaßen:
A. Klicken Sie in der Menüleiste auf ANALYSIEREN - DESKRIPTIVE STATISTIKEN - HÄUFIGKEITEN.
B. Fügen Sie im Feld Variablen die Variable ein, von der Sie eine Häufigkeitstabelle erstellen möchten.
C. Klicken Sie auf OK.
Sie erhalten dann z.B. folgende Ausgabe:
Sie sehen, dass SPSS in der ersten Spalte die Ausprägungen der Variable anbietet, in der Spalte Häufigkeit die absolute Häufigkeit, mit welcher diese Ausprägung auftritt. Unter Prozent finden Sie die prozentuellen Anteile der absoluten Häufigkeiten der Ausprägungen an der Stichprobengröße (N ist hier 154).
Links unten sehen Sie das Label Fehlend. Hier wird die Zahl der bei dieser Frage nicht vorhandenen Antworten vermerkt (Im Fall dieser Stichprobe haben 23 Personen diese Frage nicht beantwortet). Da daher die eigentliche Größe der Stichprobe bei 131 liegt (154 weniger 23 Nichtbeantwortende), verändern sich auch die realen Prozentwerte, wie in der Spalte Gültige Prozente ersichtlich. Die Spalte Kumulierte Prozente gibt die in Prozenten ausgedrückte akkumulierte Häufigkeit an und basiert ebenfalls auf den bereinigten Werten (also minus die Null- Einträge).
Bereits in der Standard-Vorgabe rechnet SPSS daher alle für eine Häufigkeitstabelle notwendigen Analysen. Werfen Sie auch einen Blick auf die fakultativen Auswahlmöglichkeiten unter Statistik und Diagramme. SPSS kann mit wenigen Arbeitsgängen äußerst umfangreiche Berechnungen durchführen.
3.2.2.2 Grafische Darstellung mit SPSS
Klicken Sie auf ANALYSIEREN - DESKRIPTIVE STATISTIK - HÄUFIGKEITEN und wählen Sie dort die Variable aus, deren Häufigkeitsverteilung Sie grafisch darstellen möchten.
Klicken Sie dann auf Diagramme. Sie haben nun die Auswahlmöglichkeit zwischen Balkendiagrammen[1], Kreisdiagrammen[2] und Histogrammen[3]. Je nach Datenlage sollten Sie unterschiedliche Diagrammtypen heranziehen. Siehe dazu den Punkt Diagramme[4].
Verweise:
[1] Siehe Kapitel 3.6.1.3
[2] Siehe Kapitel 3.6.1.1
[3] Siehe Kapitel 3.6.1.5
[4] Siehe Kapitel 3.6.2
3.2.3 Klassenbildung (Gruppierung) von Daten
Unter der Gruppierung von Daten verstehen wir die Zusammenfassung von verschiedenen Ausprägungen zu Klassen. Eine Klasse ist die Menge sämtlicher Messwerte, die innerhalb festgelegter Grenzen liegen. Dadurch kann die Häufigkeitsverteilung[1] einer Variablen mit einer Vielzahl unterschiedlicher Ausprägungen übersichtlicher dargestellt werden.
Beispiel: Gemessene Körpergrößen und Umwandlung in Klassen
Ein Beispiel wären Größenangaben in cm. Wollte man statistische Aussagen über die Körpergrößen von ÖsterreicherInnen machen, müsste man wahrscheinlich (bei einem Alter ab 14) etwa 90 verschiedene Werte angeben (von 1,20 bis 2,19). Eine derartige Tabelle wäre unübersichtlich und würde über mehrere Seiten führen:
Die Klassenbreite ist bei diskreten Variablen[2] die Anzahl der in der Klasse zusammengefassten Messwerte. Berechnet wird sie mit: Höchster Wert der Klasse minus höchstem Wert der vorausgegangenen Klasse (hier also mit z.B. 1,89 m- 1,79 m= 0,10 m).
Die (exakten) Klassengrenzen (Intervallgrenzen) sind die kleinsten bzw. größten Messwerte einer Klasse (hier also z.B. 1,70 m und 1,79999 =1,8 m).
Bei richtiger Klassenbreite sollten keine leeren Klassen (Häufigkeit = 0) auftreten. Um Ausreißer mitbehandeln zu können, könnte man die untersten und obersten Klassen offen machen: z.B. „kleiner als 1,30 m“ statt „1,20-1,29 m“ bzw. „größer als 2,09 m“ statt „2,10-2,19 cm“.
Die Klassenmitte ist der Durchschnitt des kleinsten und des größten Wertes einer Klasse. Die Klassenmitte von 1,50-1,5999 periodisch wäre daher 1,55 m. Die Klassenmitte wird für spätere Berechnungen von Bedeutung sein (z.B. für Durchschnittsberechnungen).
Verweise:
[1] Siehe Kapitel 3.1.3
[2] Siehe Kapitel 3.1.1.2
3.2.3.1 Gruppierung mit SPSS
In vielen Fällen, besonders bei stetigen Variablen[1], wird die Zahl der Ausprägungen einer Variablen so groß sein, dass Häufigkeitsverteilungen[2] unübersichtlich werden. Im folgenden Beispiel wurde die Altersverteilung der Antwortenden abgefragt:
Es wäre deutlich übersichtlicher, diese Werte in eine kleine Zahl von Klassen umzukodieren. Dazu benützen Sie die Funktion TRANSFORMIEREN - UMCODIEREN[3] in der Menüleiste. Nun können Sie sich entscheiden zwischen einer Umcodierung in die gleiche oder in eine andere Variable. Es ist besser, sich für eine andere Variable zu entscheiden, da durch die Umcodierung (man kann auch mehrere Werte zu einem einzigen neuen umcodieren) Informationsverlust auftreten kann (ob willentlich oder durch einen Bedienungsfehler). Dieses Problem wird durch Umcodierung in eine neue Variable ausgeschlossen.
Sie wählen nun die Variable aus, welche umcodiert werden soll und geben im Feld Ausgabevariable einen neuen Namen dafür ein, der aus Gründen der Kompatibilität mit älteren Programmen acht Zeichen nicht überschreiten darf. Im Feld darunter können Sie jedoch einen beliebig langen und expressiveren Namen wählen.
Klicken Sie nun auf Alte und neue Werte. Da Sie mehrere (numerische) Werte zu einem einzigen neuen zusammenfassen möchten, können Sie jeweils einen Bereich angeben (z.B. Bereich 20 bis 29), wenn Sie alle zwischen 20- 29jährigen in eine einzige Altersklasse ’zwischen 20 und 30 einbringen möchten’). Klicken Sie nach jeder einzelnen Angabe zur Umcodierung auf Hinzufügen. Für die unterste Klasse (alle unter 20jährigen wählen Sie Bereich, KLEINSTER bis Wert: (hier würden Sie 19 eingeben). Für die über 70jährigen bilden Sie eine offene Klasse, dazu wählen Sie Bereich, Wert bis GRÖSSTER: und geben hier 70 ein.
Klicken Sie am Ende auf Weiter und dann auf OK. Ihre Daten werden nun in die neue Variable umcodiert.
Die neue Häufigkeitstabelle sieht jetzt folgendermaßen aus:
Nun müssen wir die neuen Werte, ausschließlich für die Ausgabe von SPSS, rückcodieren, um die Tabelle informativer zu machen, da wir nicht sofort erkennen können, dass 0 für ’unter 20’ steht. Damit SPSS intern mit den numerischen Daten rechnen kann, wir jedoch bei allen Ausgaben (Diagramme[4], Analysen etc.) informative Bezeichnungen erhalten, klicken wir in SPSS unten links auf die Variablenansicht. Im neuen Fenster finden wir bei der neuen Variable das Attribut Variablenlabel. Nach Doppelklick darauf erscheint folgendes Fenster:
Wir geben nun die gewünschten Labels für die numerischen Daten ein, also z.B. 20-29 für die Zahl 1 usw. Nach Eingabe aller automatisch durchzuführenden Änderungen klicken wir auf OK.
Wenn wir nun die gleiche Häufigkeitsberechnung wie oben durchführen, erhalten wir nun folgende leichter verständliche Tabelle:
Verweise:
[1] Siehe Kapitel 3.1.1.2
[2] Siehe Kapitel 3.1.3
[3] Siehe Kapitel 2.2.3.2
[4] Siehe Kapitel 3.6
3.2.4 Häufigkeitsdarstellung bei Mehrfachantworten mit SPSS
Falls Sie bei einer Frage explizit Mehrfachantworten zugelassen haben, können Sie deren Häufigkeiten mit SPSS komfortabel tabellarisch darstellen.
1. Definition eines Mehrfachantwortensets
Sie müssen dazu zuerst ein (Mehrfachantworten-)Set definieren:
Klicken Sie in der Menüleiste auf ANALYSIEREN - MEHRFACHANTWORT - SET DEFINIEREN. Dann öffnet sich folgendes Fenster:
Führen Sie bitte folgende Schritte durch:
A. Sie wählen verschiedene dichotome Variable aus, die Sie in Variablen im Set einfügen;
B. Tragen Sie unter Gezählter Wert die Zahl 1 ein (d.h. dass jede Ja-Stimme einen Punkt zählt);
C. Sie lassen die Standardauswahl Dichotomien bei Variablen kodiert als;
D. Sie wählen einen Kurznamen (max. acht Zeichen für das Set) und tragen ihn unter Name ein;
E. Sie tragen unter Beschriftung einen längeren Namen ein, welcher die Tabelle anschaulich beschriften soll.
F. Klicken Sie nun auf Hinzufügen und letztendlich auf Schließen.
Das Set ist nun definiert, Sie können zur Analyse gehen:
2. Analyse
A. Klicken Sie auf ANALYSIEREN - MEHRFACHANTWORT - HÄUFIGKEITEN. Das folgende Fenster öffnet sich:
B. Wählen Sie das Mehrfachantworten-Set, welches Sie angelegt haben und ziehen Sie es in das Feld Tabelle(n) für:
C. Klicken Sie auf OK. Die Analyse wird durchgeführt:
3.3 "Mittelwerte": Lagemaße und Maßzahlen der zentralen Tendenz
Lagemaße beschreiben das Zentrum einer Verteilung durch eine Kennzahl.
Wenn wir von einem Land wissen, dass seine EinwohnerInnen durchschnittlich 2000 € monatlich verdienen, dann liefern uns Lagemaße eine erste ungenaue Idee, wo sich die EinwohnerInnen des Landes einkommensmäßig im Weltmaßstab einordnen lassen, sie ’liegen’ in der Gruppe der reicheren Länder.
Lagemaße werden oft auch als Maßzahlen der zentralen Tendenz bezeichnet. Die am häufigsten benutzten Lagemaße sind das arithmetische Mittel, das geometrische Mittel, der Median und der Modalwert.
- Das arithmetische Mittel bezeichnet den Durchschnittswert aller Einträge,
- das geometrische Mittel bezieht sich auf den Durchschnittswert voneinander abhängiger Werte (die sich also gegenseitig beeinflussen),
- der Median kennzeichnet die Normalität (welcher Wert befindet sich größenmäßig wirklich in der Mitte der Einträge und entspricht somit am ehesten dem ’Normalfall’),
- der Modalwert bezeichnet ausschließlich den am häufigsten vorkommenden Wert, der keinerlei Hinweis über die Eigenheiten der anderen Werte gibt.
Je nach Verteilung[1], Skalenniveau[2] und Art der Daten[3] sind unterschiedliche Lagemaße sinnvoll. Bei gegebener Normalverteilung[4] stimmen sowohl Median wie auch der Modalwert mit dem Arithmetischen Mittel überein. In schiefen Verteilungen hingegen nehmen sie sehr unterschiedliche Positionen ein. In rechtsschiefen Verteilungen (der Abfall erfolgt nach rechts) ist der Modalwert am kleinsten, danach kommt der Median, am größten ist der Mittelwert. In linksschiefen Verteilungen ist es umgekehrt.
Verweise:
[1] Siehe Kapitel 3.1.3
[2] Siehe Kapitel 3.1.2
[3] Siehe Kapitel 3.1.1
[4] Siehe Kapitel 3.1.3.1
3.3.1 Modalwert
Unter einem Modalwert versteht man die am häufigsten vorkommende Ausprägung einer Variable.
Beispiel:
In der folgenden geordneten Zahlenreihe 2, 3, 3, 3, 4, 4, 5, 6, 7 wäre 3 der Modalwert (weil diese Zahl dreimal auftritt, häufiger als jede andere Zahl).
Mittelung bei benachbarten gleichgroßen Werten
Falls mehrere benachbarte Werte die größte Häufigkeit aufweisen, so wird ihr arithmetisches Mittel berechnet. Haben z.B. die Werte 5 und 6 gleichermaßen die größte Häufigkeit, so ist der Modalwert der Durchschnitt dieser beiden Werte.
Beispiel:
In der Zahlenreihe 2, 3, 3, 3, 4, 4, 4, 5, 6, 7 liegt der Modalwert bei 3,5. Sowohl 3 wie auch 4 kommen mit jeweilig dreimaligem Auftreten häufiger als die anderen Werte vor. Das arithmetische Mittel von 3 und 4 liegt bei 3,5.
Modalklasse: Klasse mit größter Zahl an Einträgen
Bei klassierten Daten[1] ist die Modalklasse diejenige Klasse mit der größten Zahl an Einträgen
Nur selten praktische Relevanz des Modalwerts
Der Modalwert ist aussagekräftig, wenn ein einzelner Wert sehr häufig vorkommt (z.B. 27 Frauen und drei Männer) und unsinnig, wenn der häufigste Wert nur relativ selten vorkommt. Der Modalwert kann im Gegensatz zum arithmetischen Mittelwert oder zum Median auch sinnvoll in Nominalskalen[2] verwendet werden.
Verweise:
[1] Siehe Kapitel 3.2.3
[2] Siehe Kapitel 3.1.2.2
3.3.2 Arithmetisches Mittel
Das arithmetische Mittel ist die Summe aller Messwerte geteilt durch deren Anzahl:
Z.B. die durchschnittliche Zahl von Schafen der Bauern im Dorf Nkorongoji in Mali: Die Messwerte sind: 5, 12, 3, 4, 7, 6. Die Summe ist 37, die Zahl der Messwerte ist 6, also ist das arithmetische Mittel 37/6= 6,17.
Arithmetisches Mittel bei Einteilung der Messwerte in Klassen:
Wenn die Daten zahlreicher sind bzw. bereits in Klassen[1] eingeteilt wurden, kann man das arithmetische Mittel einfacher berechnen: man multipliziert in jeder Klasse die Klassenmitte (Durchschnitt aus dem theoretisch kleinstem und größten Wert einer Klasse) mit der Zahl der Einträge in der jeweiligen Klasse:
Der Durchschnitt, in diesem Fall das durchschnittliche Gehalt, wäre somit 14500/17= 852,94.
Das arithmetische Mittel stößt bei bestimmten Datenlagen jedoch auch auf einige Probleme.
Verweise:
[1] Siehe Kapitel 3.2.3
3.3.3 Median
Der Median ist jener Wert, welcher in einer größenmäßig geordneten Reihe genau in der Mitte liegt. D.h. oberhalb wie unterhalb von ihm befindet sich eine gleichgroße Anzahl von Einträgen.
Warum benötigen wir ihn, da es doch auch das arithmetische Mittel[1] gibt? Das arithmetische Mittel ist der Mittelwert, der sich ergibt, wenn wir eine Summe durch die Anzahl der gezählten Elemente dividieren.
Beispiel: Verzerrung durch Mittel, nicht aber durch Median
Die folgende Grafik zeigt das individuelle Einkommen der EinwohnerInnen des fiktiven Ortes Largebread im Jahr 2002:
Das durchschnittliche Einkommen von etwa 26000 $ scheint die Einkommenssituation der EinwohnerInnen von Largebread gut zu beschreiben. Die Normalverteilungskurve[2] zeigt uns an, dass das Einkommen relativ gut normalverteilt ist.
Was würde aber jetzt passieren, wenn der reichste Mann der Welt, Bill Gates, sich plötzlich entschließen würde, nach Largebread zu ziehen? Bill Gates verfügt über ein Jahreseinkommen von 5 Milliarden $. Das Diagramm verändert sich extrem:
Haben ohne Bill Gates die 1100 EinwohnerInnen von Largebread durchschnittlich 26064 $ im Jahr verdient, so sind sie nun scheinbar über Nacht reich geworden und verdienen mit Bill Gate nun durchschnittlich fast 5 Millionen Dollar im Jahr. Man sieht deutlich, dass einzelne "Ausreißer" wie Bill Gates einen derartigen Durchschnittswert unsinnig machen können. Zur Beschreibung der Realität von Largebread ist daher ein Indikator für das durchschnittliche Einkommen deutlich besser geeignet, welcher Ausreißer nicht berücksichtigt, nämlich der Median: Das Durchschnittseinkommen in Largebread, berechnet nach dem Median, liegt ohne Bill Gates bei 26.000 und auch mit ihm nur bei 26.000 $.
Probleme des Arithetischen Mittel:
Das arithmetische Mittel stößt somit an seine Grenzen:
- wo extreme Grenzwerte auftreten (wie in Largebread),
- bei sehr kleiner Beobachtungszahl (einzelne Werte können besonders leicht den Durchschnittswert verzerren),
- bei Verteilungen mit offenen Klassen (Schwierigkeit der Bestimmung der Klassenmitte der offenen Klassen),
- bei Ordinalskalen[3] (hier sollte er nicht verwendet werden).
In all diesen Fällen ist es genauer, zum Median zu greifen. Der Median ist der Wert, der in einer geordneten Liste (oder primären Tafel) genau in der Mitte liegt, d.h. dass sich genauso viele Werte oberhalb wie unterhalb des Wertes befinden. Dieser Wert liegt an (n+1)/2ter Position. Hat man 3 Werte, dann ist der Medien der 2. Wert ([3+1]/2).
Berechnung des Median bei Urliste:
- Werte nach Größe rangreihen,
- mittleren Wert nehmen,
- liegt der Median zwischen 2 Werten (wenn Median nicht ganze Zahl ist), dann wird der Durchschnitt der ihn umgebenden 2 Werte genommen.
z.B. Schulnoten 3,2,2,5,1,1,2,5 -> Rangreihung: 1,1,2,2,2,3,5,5 -> Der 4,5. Wert (Durchschnitt aus 2+2) ist der Median, also 2.
Verweise:
[1] Siehe Kapitel 3.3.2
[2] Siehe Kapitel 3.1.3.3.1
[3] Siehe Kapitel 3.1.2.3
3.3.3.1 Median bei gruppierten Daten
Bei gruppierten Daten ist die Berechnung des Medians ein wenig komplizierter. Hier ist die rechnerische Abfolge:
- Bildung der Häufigkeitstabelle (inklusive kumulierter Häufigkeiten)
- Ermittlung der Klasse m, in welcher der Median steckt: wo liegt der Wert (n+1)/2. Diese wird nun als Medianklasse bezeichnet (n= Gesamtanzahl der Einträge)
- Ermittlung der unteren (=xmu) und oberen Klassengrenze (x) von m
- Ermittlung der Klassenbreite h (ergibt sich aus obere Klassengrenze - untere Kl.Grenze) .
- Subtraktion der akkumulierten Häufigkeit aller Klassen bis zur Klasse m (d.h. die Klassen 1 bis m-1) von n/2 -> Position des Medians in der Medianklasse
- Division der Position durch die Zahl der Werte der Klasse = relative Größenordnung des Medians (Anteile vom Ganzen der Klasse)
- Multiplikation des relativen Klassenanteils mit der Klassenbreite = absolute Größenordnung des Medians innerhalb der Klasse
- Addition der unteren Klassengrenze (in welcher der Median liegt) zur absoluten Größe des Medians (in der Klasse) = Endergebnis = Median Z
Beispiel: Zeitverbrauch bei Lösung einer Aufgabe
n=37, Median ist also der 18. Wert, dieser liegt in der Klasse 5 (4,5-5,5 Minuten Dauer), daher:
Der Median liegt somit bei 5.
3.3.4 Geometrisches Mittel
Das geometrische Mittel ist der Mittelwert bei mathematischen Produkten, wie z.B. bei Wachstums- oder Zinsfaktoren. Das geometrische Mittel kann nur bei Proportionalskalen[1] verwendet werden. Dieses wird als n- te Wurzel aus der relativen Veränderung (Endwert dividiert durch Anfangswert) berechnet, wobei n der Zahl der Zeiteinheiten entspricht.
Beispiel: durchschnittliche Inflationsrate
Nehmen wir an, die jährliche Inflationsrate hätte durch 10 Jahre hindurch jeweils 2 % pro Jahr betragen. Hier wäre es falsch anzunehmen, dass die Inflation nach den 10 Jahren um 20 % höher als davor liegt, da sich die Werte gegenseitig beeinflussen. Im ersten Jahr sind es 2 % Inflation von 100 %; im 2. Jahr 2 % von 102 % (also 2,04 % Preissteigerung verglichen mit dem Ausgangsjahr), im 3. Jahr 2 von 104,04 (= 2,0808 % vergleichen mit dem Ausgangsjahr).
Ähnlich müssen wir zurückrechnen, wenn wir von einem bestimmten Preisniveau nach 10 Jahren auf die durchschnittliche Inflationsrate dieser 10 Jahre schließen wollen.
Errechnung der durchschnittlichen Inflationsrate
Der Lebenshaltungskostenindex liegt 2006 bei 136,5, vor 10 Jahren lag dieser bei 100. Somit erfolgte eine Preissteigerung von 36,5 % im Laufe der letzten 10 Jahre. Es wäre hier falsch, als durchschnittliche Preissteigerung/Jahr den Wert 3,65 % anzunehmen (36,5 % durch die Zahl der Jahre, also 10, dividiert), da sich die Werte gegenseitig beeinflussten (multiplizierten).
Den richtigen Wert erhält man, wenn man die 10. Wurzel (da 10 Jahre) aus dem Gesamtveränderungsfaktor zieht. Diesen erhält man, indem man den Endwert durch den Ausgangswert dividiert: 136,5 dividiert durch 100 ist 1,365. Die 10.Wurzel daraus ist 1,0304. 100 multipliziert mit 1,024*1,0304*1,0304 etc. (insgesamt 10x damit multipliziert) ergibt nach 10 Jahren 136,5.
Die Differenz zu 1 multipliziert mit 100 (es handelt sich ja um Prozente, bisher sind es nur Teile vom Ganzen) ist 0,0304*100 = 3,04 % jährliche Preissteigerung (und nicht 3,65, wenn wir das rein arithmetische Mittel genommen hätten).
Verweise:
[1] Siehe Kapitel 3.1.2.5
3.3.5 Harmonisches Mittel
Das harmonische Mittel ist ein geeignetes Lagemaß für Größen, die durch einen (relativen) Bezug auf eine Einheit definiert sind: z.B. Geschwindigkeiten (Strecke pro Zeiteinheit) oder Ernteerträge (Gewicht oder Volumen pro Flächeneinheit).
Die zur Berechnung benötigte Formel ist:
Beispiel: Durchschnittsreisegeschwindigkeit
Elke fährt von Wien nach Melk (etwa 100 km) mit einer Durchschnittsgeschwindigkeit von 80 km/h. Anschließend fährt sie mit durchschnittlich 120 km/h von Melk nach Linz und legt dabei ebenfalls 100 km zurück. Wie schnell fuhr sie im Schnitt?
Die meisten Befragten würden nach kurzer Überlegung 100 km/h als Durchschnittsgeschwindigkeit angeben. Doch ist dies falsch, da Elke unterschiedlich lange mit diesen beiden Geschwindigkeiten unterwegs war. Elke braucht für die ersten 100 km, die sie mit 80 km/h zurücklegt, insgesamt 100/80 Stunden, also 1,25 Stunden oder 1 Stunde und 15 Minuten. Für die zweiten Hundert Kilometer, die sie mit 120 km/h zurücklegt, benötigt sie 100/120 Stunden, also 5/6 Stunden oder 50 Minuten. Insgesamt legte sie somit 200 km in einer Zeit von 2,083 Stunden zurück (2 Stunden und 5 Minuten). 200 km dividiert durch die Zeit, die sie dafür benötigte, ergibt nun eine Durchschnittsgeschwindigkeit von 96,02 km/h.
3.3.5.1 Harmonisches Mittel mit SPSS
Legen Sie zwei Variable an.Variable 1 für die Distanz, Variable 2 für die Geschwindigkeit. Nach Eingabe der Werte klicken Sie auf ANALYSIEREN - MITTELWERTE VERGLEICHEN - MITTELWERTE und geben dort unter Abhängige Variable die Geschwindigkeit ein, unter Unabhängige Variable die Distanz.
Klicken Sie dann auf Optionen und wählen Sie im nächsten Fenster das Harmonische Mittel aus. Fertig.
3.3.6 Wann welche Lagemaße?
Die Zahl in Klammern gibt die Priorität an. X(1) wird daher als wichtiger als X(2) eingestuft. Fett markiertes X bezeichnet Kennzahlen, welche bei der gegebenen Datenart absolut sinnvoll sind, nicht fettes X liefert mögliche, aber nicht besonders sinnvolle oder teilweise sogar in die Irre führende Werte.
Während Lagemaße bei eingipfeligen symmetrischen[1] Daten weitgehend übereinstimmen und typisch für die Daten sind, sind sie bei anderen Verteilungsformen[2] (U-förmige, sehr schiefe, mehrgipfelige, gleichverteilte) nicht aussagekräftig für die Verteilung.
Verweise:
[1] Siehe Kapitel 3.1.3.1
[2] Siehe Kapitel 3.1.3.2
3.3.7 Berechnung von Lagemaßen mit SPSS
Während das geometrische Mittel[1] mit jedem mathematischen Taschenrechner leicht berechnet werden kann (einfach n-te Wurzel aus der Endzahl), sind die Lagemaße mit SPSS sehr einfach zu berechnen.
Klicken Sie in der Menüleiste auf ANALYSIEREN - HÄUFIGKEITEN und wählen Sie dann Statistik aus:
Nun können Sie alle Lagemaße auswählen, den Mittelwert, den Median und den Modalwert. Das folgende Resultat stammt aus der Berechnung der Lagemaße des Bruttonationalprodukts der Länder dieser Welt im Jahr 1995 (world95.sav).
Wir sehen, dass die Lagemaße extrem auseinanderliegen. Warum, macht das Histogramm[2] mit Normalverteilungskurve[3] (anklicken unter Diagramme) sofort sichtbar: Eine kleine Zahl von reichen Ländern hebt das arithmetische Mittel auf ein Niveau, welches außerhalb der Reichweite der meisten Länder dieser Welt liegt:
Wäre es eine Normalverteilung, würden im Bereich (Artithm. Mittel +/s s) 68 % aller Werte liegen. Zieht man jedoch die Standardabweichung s (= 6479) vom Mittelwert ab, gelangt man am linken Rand bereits in den negativen Einkommensbereich. Auch dies zeigt die Sinnlosigkeit der Verwendung des arithmetischen Mittels bei diesen Daten. Der Median hingegen bildet hier die Realität mit knapp 3000 $ wesentlich besser ab.
Verweise:
[1] Siehe Kapitel 3.3.4
[2] Siehe Kapitel 3.6.1.5
[3] Siehe Kapitel 3.1.3.1
3.4 Streuungsmaße oder ’Wie allgemeingültig ist der Mittelwert’
Streuungsmaße informieren über die Verteilung von Ausprägungen außerhalb des Zentrums. Sie liefern dadurch wertvolle Informationen über die (Un-)Ausgeglichenheit einer Verteilung.
Grafische Darstellung der Streuung durch Histogramme
Histogramme[1] zeigen die relative "Gerechtigkeit" einer Verteilung in graphischer Form, wie z.B. das folgende über das Bruttonationalprodukt der Länder dieser Welt im Jahr 1991.
Dieses Histogramm zeigt optisch deutlich, dass im Jahr 1991 das durchschnittliche Bruttonationalprodukt von 5860 $ für die meisten Länder unerreichbar fern lag und damit keinerlei Aussagekraft für ihre Realität hatte. Der Median[2] lag damals bei der Hälfte des Mittelwerts[3], nämlich bei 2995 $. Ein Viertel der Länder wies ein Bruttonationalprodukt auf, welches unter 996 $ lag, ein Fünftel unter 681 $, ein Zehntel der Länder dieser Welt sogar unter 323 Dollar.
Lagemaße zeigen oft nur verzerrtes Bild der Realität bzw. Normalität
Man ersieht daraus, dass Kennzahlen wie das arithmetische Mittel[4] oft nur wenig geeignet sind, die Normalität darzustellen, d.h. dass der Wert des arithmetischen Mittel erheblich von der Realität der meisten Ausprägungen verschieden sein kann.
Wir benötigen daher weitere Kennzahlen, sogenannte Streuungsmaße, um Auskunft über die Randbereiche der Ausprägungen zu erhalten. Dazu zählen besonders die Standardabweichung und Perzentile bzw. Quartile[5].
Verweise:
[1] Siehe Kapitel 3.6.1.5
[2] Siehe Kapitel 3.3.3
[3] Siehe Kapitel 3.3.2
[4] Siehe Kapitel 3.3.2
[5] Siehe Kapitel 3.4.3.1
3.4.1 Varianz
Die Varianz ist eine Kennzahl, welche die Streuung aller Daten berücksichtigt. Sie wird berechnet, indem man den Durchschnitt der quadrierten Abweichung vom Arithmetischen Mittel[1] berechnet.
Je größer die Varianz verglichen mit dem Arithmetischen Mittel, desto stärker sind die Abweichungen der einzelnen Messwerte von diesem.
Ein Beispiel: Ein Arithmetisches Mittel von 100 kann sich ergeben, wenn alle Einträge der Zahl 100 entsprechen. Alle Einträge hätten dann eine Abweichung von 0 vom Arithmetischen Mittel, damit natürlich dann auch deren Quadrate sowie der Summen der Quadrate. Die Varianz wäre dann 0 und würde eine komplette Übereinstimmung aller Werte mit dem Arithmetischen Mittel anzeigen.
Ein Arithmetisches Mittel von 100 kann sich auch ergeben, wenn die Hälfte der Werte bei 0 und die andere Hälfte bei 200 liegt. In diesem Falle hätten wir eine extrem große Varianz (jeweils eine Abweichung von 100 vom Arithmetischen Mittel, diese wird quadriert, die Ergebnisse zusammengezählt und durch N dividiert. In diesem Falle erhielten wir eine Varianz von 10.000, Ausdruck der maximalen individuellen Abweichung der Meßwerte vom Arithmetischen Mittel.
In der Praxis verwendet man vor allem die Wurzel aus der Varianz, die sogenannte Standardabweichung[2].
Verweise:
[1] Siehe Kapitel 3.3.2
[2] Siehe Kapitel 3.4.2
3.4.2 Standardabweichung
Die Standardabweichung s gibt in einer Normalverteilung[1] einen Bereich um den Mittelwert[2] an, innerhalb dessen sich 68,2 % aller Einträge befinden. Innerhalb des Bereichs Mittelwert +/-2s befinden sich in einer Normalverteilung 95,44 % aller Einträge. Berechnet wird die Standardabweichung als Wurzel aus folgender Formel:
Beispiel: Intelligenzquotient (Durchschnitt = 100, s= 15).
Kenntnis der Standardabweichung = Kenntnis des Verlaufs der Verteilung
Auch wenn man die grafische Darstellung der Häufigkeitsverteilung, wie z.B. mit einem Histogramm[3], nicht kennt, kann man sie aufgrund der Kenntnis des Mittelwerts und der Standardabweichung weitgehend vorhersagen. Hat man einen Mittelwert von 100 und eine Standardabweichung von 10, wird die Verteilungskurve deutlich steiler sein, als wenn die Standardabweichung bei 30 liegt.
Kenntnis der Standardverteilung = Abschätzung der Häufigkeit von Ausprägungen
Die Kenntnis der Standardverteilung erlaubt uns, die Häufigkeit von Ausprägungen sofort einschätzen zu können. Wenn z.B. wie oben bekannt ist, dass der durchschnittliche Intelligenzquotient bei 100, die Standardabweichung bei 15 liegt, dann kann man sofort abschätzen, wie ein bestimmter Intelligenzquotient einzustufen ist. Wenn eine Person X einen IQ von 130 aufweist, dann liegt dieser beim Mittelwert +2 Standardabweichungen. Daher kann man sofort abschätzen, dass der betreffende IQ höher ist als 98 % aller Einträge.
Erklärung:
95,44 % aller Einträge befinden sich im Bereich Mittelwert ±2s, d.h. 4,56 % liegen außerhalb dieses Bereichs. In unserem Beispiel würden 95,44% aller Werte zwischen 70 und 130 liegen, Die restlichen 4,56 % teilen sich zu gleichen Teilen auf die darunter und darüber liegenden Bereiche auf. Somit bleiben für den Bereich ab 130 insgesamt 2,28 % aller Einträge übrig.
Verweise:
[1] Siehe Kapitel 3.1.3.1
[2] Siehe Kapitel 3.3.2
[3] Siehe Kapitel 3.6.1.5
3.4.3 Perzentile
Perzentile teilen die Ausprägungen der Variablen in gleich große Gruppen, sodass sich in jeder Gruppe der gleiche Prozentsatz an Einträgen befindet.
Besonders beliebt dabei sind die Quartile (= Viertel, jeweils 25 %). Bei Dezilen handelt es sich hingegen um Gruppen von jeweils 10 % der Werte.
3.4.3.1 Quartile
Quartile teilen die Verteilung in vier gleich große Viertel: 25 % der Werte sind kleiner oder gleich groß mit dem 1. Quartil, 50 % sind kleiner oder gleich groß wie das 2. Quartil (daher ist das 2. Quartil gleichzusetzen mit dem Median), 75 % sind kleiner oder gleich groß mit dem 3. Quartil. Quartile sollten erst ab einer Stichprobengröße[1] von zumindest 20 eingesetzt werden.
Verweise:
[1] Siehe Kapitel 2.1.1
3.4.3.1.1 Die Ermittlung von Quartilen
Die Ermittlung von Quartilen (gewichtet):
- man reiht die Werte nach ihrer Größe (unser Beispiel: Besitz von Büchern zur Ethnologie)
z.B. 1, 2, 3, 3, 5, 7, 11, 16, 17, 17, 20, 22, 25, 48, 52, 56, 76, 89, 96, 115
20 verschiedene Einträge liegen vor, daher ist n=20.
- Berechung des 1. Quartils, d.h. der Wert, welcher größer als 25 % und kleiner als 75 % aller Werte ist. Q1 liegt an der (n+1)/4. Stelle
Dieser Wert liegt in unserem Beispiel an der (n+1)/4 Stelle = 5.25, also zwischen dem 5. Wert (=5) und dem 6. Wert (=7). Der Bruchteil (0,25) gibt an, dass zum Wert von 5 noch ¼ des Abstands zwischen 5 und 6 hinzukommt. Q1 ist daher 5 + 0,25*2 = 5,5.
- Berechnung des 2. Quartils (wird berechnet wie der Median). Dieser liegt zwischen der 10. und 11. Stelle, daher ist der Wert zu mitteln (17+20)/2 = 18,5
- Berechnung des 3. Quartils, d.h. der Wert, welcher größer als 75 % und kleiner als 25 % der sortierten Werte ist. Q3 = 3*(n+1)/4
In unserem Beispiel: Q3 = 3*21/5 = 15,75. Stelle. Q3 liegt zwischen dem 15. Wert (= 52) und dem 16. Wert (= 56). Der Bruchteil (0,75) gibt an, dass zum 15. Wert noch ¾ des Abstands zwischen dem 15. und dem 16. Wert hinzukommen, daher: Q3 = 52 + 0,75*4 = 55.
Wir können nun die Aussage machen, dass Personen aus dem ersten oder untersten Quartil (Viertel) weniger als 5,5 Bücher, aus dem obersten Quartil hingegen mindestens 55 Bücher besitzen.
3.4.4 Berechnung von Streuungsmaßen mit SPSS
SPSS ermöglicht es, alle Arten von Streuungsmaßen mit wenigen Tastenklicks gleichzeitig zu berechnen.
Dazu genügt es, auf ANALYSIEREN - DESKRIPTIVE STATISTIKEN - HÄUFIGKEITEN zu klicken, dann links unten nochmals auf Statistik zu klicken und im neuen Fenster alle nur denkbaren Kennzahlen für Lage- und Streuungsmaße anzuwählen:
Für die Berechnung von Quartilen[1] genügt das Setzen eines Häkchens in Quartile, möchte man Dezile (also in 10%-Gruppen) berechnen, gibt man im Feld Trennwerte für die Zahl 10 ein (dadurch werden 100 % auf 10 gleiche Gruppen aufgeteilt, also besteht jede Gruppe aus 10 %). Gibt man einen Wert X im Feld neben Perzentile ein und klickt auf Hinzufügen (wie z.B. die Zahl 37), so wird ermittelt, unterhalb welchen Kennwerts X % der Einträge liegen (in diesem Fall 37 %). Man kann beliebig viele dieser Perzentile setzen.
SPSS bietet die Berechnung und Darstellung von Streuungsmaßen in einer Vielzahl statistischer Verfahren an, meist unter einem Auswahlpunkt Statistik.
Verweise:
[1] Siehe Kapitel 3.4.3.1
3.4.5 Vergleichende grafische Darstellung von Streuung und Lage mit Box-Plots
Boxplots sind konzentrierte grafische Darstellungen von Lage und Streuung. Boxplots geben einen exzellenten optischen Überblick über wesentliche Parameter von Lage und Streuung, wie das Arithmetisches Mittel, die Quartile sowie über die Grenzwerte nach unten wie nach oben, wobei Ausreißer spezifisch markiert werden.
Informationen der Boxplots:
Boxplots enthalten eine Fülle von Hinweisen, wie im obigen Diagramm:
A. ein Kästchen, welches den Abstand zwischen dem 1. und dem 3. Quartil[1] markiert (Streuung)
B. eine langgezogene Linie, die von Extremwert zu Extremwert führt: Range (Streuung);
C. Einen Querstrich im Kästchen, welcher das Arithmetische Mittel[2] markiert;
D. Mit * bezeichnete Einträge, welche mehr als 3 Kästchenlängen entfernt liegen (Ausreißer).
E. Mit Kreis gekennzeichnete Einträge liegen 1,5-3 Kästchenlängen entfernt.
F. Neben diesen Ausreißern steht auch jeweils die Nummer des Datensatzes, in welchem diese Ausreißer gefunden werden können.
Extreme Informationsdichte durch Boxplots:
Durch diese konzentrierten Informationen erlauben Boxplots eine sehr schnelle Abschätzung sowohl der Lage wie auch der Streuung. Im obigen Boxplot, welches auf der y-Achse die Zahl der in Österreich verbrachten Jahre, auf der x-Achse das Migrationsmotiv widerspiegelt, kann man auf den ersten Blick ersehen, dass das Gros der AsylwerberInnen erst in den letzten Jahren kam, hingegen das Motiv Schulbesuch ein länger zurückliegender Migrationsgrund war. Die große Streuung (ausgedrückt durch die Länge des Kästchens) bei der Arbeitsuche gibt einen Hinweis darauf, dass viele Menschen über längere Zeit hinweg aus diesem Grund zuwanderten, während der Asylgrund einen wesentlich kürzeren Zeitraum betraf.
Verweise:
[1] Siehe Kapitel 3.4.3.1
[2] Siehe Kapitel 3.3.2
3.4.5.1 Erstellung von Boxplots mit SPSS
Klicken Sie in SPSS in der Menüleiste auf ANALYSIEREN - DESKRIPTIVE STATISTIKEN - EXPLORATIVE DATENANALYSE. Das folgende Fenster erscheint:
Sie finden links die Liste der Variablen. Übertragen Sie ins Feld Abhängige Variablen die Variable, deren Lage und Streuung Sie mittels eines Boxplots darstellen möchten. Beachten Sie bitte, dass es sich dabei zwingend um eine metrische Variable[1] handeln muss. Falls Sie die Lage[2] und Streuung[3] der gesamten Einträge dieser Variablen wiederspiegeln möchten, können Sie auf OK klicken. Das Boxplot erscheint in der Ausgabe nach einer Reihe statistischer Berechnungen.
Möchten Sie den Einfluss einer anderen Variable auf die gewählte Variable untersuchen, dann fügen Sie diese Variable in das Feld Faktorenliste ein. Sie erhalten dann verschiedene Boxplots, die jeweils Subgruppen der abhängigen Variablen bezeichnen:
Verweise:
[1] Siehe Kapitel 3.1.1.1
[2] Siehe Kapitel 3.3
[3] Siehe Kapitel 3.4
3.5 Der Zusammenhang zwischen Variablen
Zu den spannendsten Fragen gehört die Untersuchung von Zusammenhängen zwischen Variablen. Es ist naheliegend, sich die Frage zu stellen, ob es z.B. einen Zusammenhang zwischen Rassismus und Bildung bzw. Sozialisation, Einkommen, Erfahrungen gibt. Es ist denkbar, dass die Religion einer Person Auswirkungen auf ihre Kinderzahl hat; es ist denkbar, dass Menschen eher zu biologischen und meist auch teureren Lebensmittel greifen, wenn auch ihr Einkommen höher ist usw.
Um derartige Zusammenhänge aufzudecken, verfügen wir über verschiedene Methoden, wie z.B. die Kreuztabellen-Analyse oder die Korrelation(en).
3.5.1 Optische Erkennung von Zusammenhängen
Optische Darstellung von Zusammenhängen: das Streudiagramm
Trägt man auf einer Matrix von links nach rechts die Ausprägungen für die Variable A ein und die Ausprägungen für die Variable B auf der Y- Achse, so erhält man eine Reihe von Schnittpunkten. Das sich aus den Schnittpunkten ergebende Diagramm wird auch Verteilungsgrafik (auch Streuungsdiagramm, Streudiagramm oder Scatterplot genannt).
Herstellung eines Streudiagramms
Streudiagramme eignen sich zur grafischen Darstellung bivariater Daten, also zur Darstellung von Wertepaaren in einem Koordinatensystem. An Lage und Dichte des Punkteschwarms lässt sich anschaulich ablesen, ob ein Zusammenhang zwischen den Variablen besteht. Sie werden folgendermaßen erstellt: Man trägt in einem Diagramm jeweils die Schnittpunkte der beiden Variablen ein, wobei der Wert der 1. Variablen auf der X- Achse, der Wert der 2. Variable auf der Y- Achse liegt. Im Beispiel unten trägt man auf der X- Achse den Alphabetisierungsgrad des Landes ein, auf der Y-Achse das Bruttonationalprodukt des gleichen Landes. Wo beide Einträge aufeinander treffen, wird eine Markierung (ein Punkt) eingefügt.
Zusammenhänge bereits visuell erkennbar
Hier erkennen wir bereits optisch einen gewissen Zusammenhang. Die meisten Schnittpunkte befinden sich links oben und gehen in einer Linie nach rechts unten. Man könnte durch die Schnittpunkte annäherungsweise eine Gerade[1] ziehen, die von rechts oben nach links unten geht. Man spricht hier von einem linearen Zusammenhang.
Die Aussage der Grafik ist: je höher der Alphabetisierungsgrad der Frauen, desto niedriger die Kindersterblichkeit.
Aus diesem Diagramm ist ersichtlich, dass ein gewisser Zusammenhang zwischen Alphabetisierungsrate und BNP besteht. Länder mit nur geringer Alphabetisierungsrate haben ausnahmslos ein sehr niedriges BNP, mit hoher Alphabetisierungsrate steigt die Wahrscheinlichkeit, auch ein sehr hohes BNP aufzuweisen, doch liegen die Werte bei hoher Alphabetisierungsrate extrem auseinander. Hier lässt sich wesentlich schwerer eine Gerade ziehen, es liegt nur mehr bedingt ein linearer Zusammenhang vor.
Nachfolgend verschiedene weitere Diagramme, welche teilweise deutliche Zusammenhänge zeigen (wie oben links) oder keinerlei Zusammenhang (wie unten links). Diskutieren Sie in der Gruppe die Art der Zusammenhänge in den restlichen Diagrammen.
Verweise:
[1] Siehe Kapitel 3.5.4.2
3.5.2 Kreuztabellen-Analyse
Unter Kreuztabellen (auch Kontingenztafeln genannt) versteht man die tabellarische Darstellung der Häufigkeiten[1], welche bei der Kombination der Ausprägungen von zwei oder mehr Variablen auftreten.
Wenn z.B. zwei Variablen vorliegen, werden die Ausprägungen der Variablen A in Spalten von links nach rechts und die Ausprägungen der Variablen B in Zeilen von oben nach unten eingetragen. In jeder einzelnen Zelle wird sodann die spezifische Häufigkeit der jeweiligen Kombination Ausprägung der Variablen A mit Ausprägung der Variablen B vermerkt.
Verweise:
[1] Siehe Kapitel 3.1.3.3.2
3.5.2.1 Berechnung von Kreuztabellen-Analysen mit SPSS
Wir möchten mit einer Kreuztabelle zeigen, wie gut in Wien lebende AfrikanerInnen nach (überprüften) Eigenangaben Deutsch beherrschen und überprüfen, ob ihre Sprachkompetenz im Deutschen mit ihrer Nationalsprache zusammenhängt.
Dazu klicken wir in SPSS auf ANALYSIEREN - DESKRIPTIVE STATISTIKEN - KREUZTABELLEN. In den Zeilen klicken wir die Herkunftssprache an, unter Spalten die Sprachkompetenz im Deutschen. Nach Klicken auf OK erhalten wir bereits folgende Tabelle:
Man kann die Ergebnisse leichter interpretieren, wenn auch die relativen Häufigkeiten[1] ermittelt werden. Dazu klicken wir unter Zellen auf zeilenweise Prozentwerte:
Nun können wir sofort erkennen, dass in unserer Stichprobe die durchschnittlichen Deutschkenntnisse der Zuwanderer aus Ländern mit französischer Nationalsprache besser als die aus Ländern mit englischer Nationalsprache sind. 70,7 % der Frankophonen sprechen besser Deutsch, aber nur 49,0 % der Anglophonen.
Verweise:
[1] Siehe Kapitel 3.1.3.3.2
3.5.2.1.1 Überprüfung von Zusammenhängen mit dem Chi-Quadrat-Test
Der Chi-Quadrat-Test, angewandt auf Kreuztabellen, ermittelt die Wahrscheinlichkeit[1], ob Zusammenhänge mehr als nur zufälliger Natur sind.
Im vorigen Beispiel (Kreuztabelle) sahen wir, dass offensichtlich ein deutlich höherer Prozentsatz von frankophonen AfrikanerInnen besser Deutsch spricht als Anglophone. Wir wissen jedoch noch nicht, ob diese Unterschiede auch signifikant sind.
Berechnung des Chi-Quadrat-Tests mit SPSS
Dazu wählen wir unter ANALYSIEREN - DESKRIPTIVE STATISTIKEN - KREUZTABELLEN den Punkt Statistik, setzen dort bei Chi-Quadrat ein Häkchen und erhalten als zusätzliche Ausgabe:
Für uns interessant ist hier der Wert für Asymptotische Signifikanz. Dort wird 0,023 aufgeführt, also ein Wert kleiner als 0,05. Damit ist mit einer Wahrscheinlichkeit von mehr als 95 % anzunehmen (oder mit einer Irrtumswahrscheinlichkeit von weniger als 5 %), dass tatsächlich ein Zusammenhang zwischen Nationalsprache und Sprachkompetenz im Deutschen besteht. Bei einem Wert > 0,01 wäre die Wahrscheinlichkeit eines Zusammenhangs sogar größer als 99 %, also wäre das Ergebnis hoch signifikant[2].
Verweise:
[1] Siehe Kapitel 1.3
[2] Siehe Kapitel 1.3.2
3.5.2.2 Grafische Darstellung von Kreuztabellen mit SPSS
Die Ergebnisse von Kreuztabellen können mit Gruppierten Balkendiagrammen[1] besonders anschaulich dargestellt werden.
Mit SPSS ist deren Erstellung sehr einfach.
Klicken Sie auf ANALYSIEREN - DESKRIPTIVE STATISTIKEN - KREUZTABELLEN und machen Sie ein Häkchen beim Punkt Gruppierte Balkendiagramme anzeigen.
Spielen Sie mit den einzelnen Elementen dieser Grafik herum. Beim Doppelklick auf Details dieses Diagramms werden sich viele Einstellmöglichkeiten öffnen.
Verweise:
[1] Siehe Kapitel 3.6.1.3
3.5.3 Die Korrelation
Unter einer Korrelation versteht man eine Kennzahl für den Zusammenhang zwischen Variablen. Prinzipiell können folgende Zusammenhänge bestehen:
- Übereinstimmung: je höher der Wert der Variablen A, desto höher ist meist auch der Wert der Variablen B: positive Korrelation
- Gegensatz: je höher Variable A, desto niedriger ist meist die Variable B: negative Korrelation
- Unabhängigkeit: Hohe Werte von A können relativ beliebigen Werten von B entsprechen und umgekehrt: keine Korrelation
Korrelationskoeffizienten können Werte zwischen -1,00 und +1,00 annehmen. Ein Wert von -1,0 bedeutet eine perfekte negative Korrelation: Hohe Werte der Variablen A gehen ausnahmslos mit niedrigen Werten der Variablen B einher und umgekehrt. Ein Wert von (+)1,0 bezeichnet eine perfekte positive Korrelation: hohe Werte von A entsprechen praktisch immer hohen Werten von B und umgekehrt.
Je nach Art der Grundskalierung[1] muss man zu unterschiedlichen Korrelationskoeffizienten greifen:
Vorsicht bei vorschneller Herstellung von Zusammenhängen
Gefundene Korrelationen müssen dennoch nochmals kritisch hinterfragt werden. Es gibt z.B. Scheinkorrelationen[2], die nur deshalb auftreten, weil beide Variablen hoch mit einer dritten Variable korrelieren, und verdeckte Korrelationen[3], bei welchen sich Subgruppen der Stichprobe[4] gegenseitig neutralisieren, selbst aber eine hohe Korrelation bei den beiden Variablen aufweisen. Erst die Signifikanz[5] gibt einer Korrelation die nötige Aussagekraft.
Verweise:
[1] Siehe Kapitel 3.1.2
[2] Siehe Kapitel 3.5.3.4.3
[3] Siehe Kapitel 3.5.3.4.2
[4] Siehe Kapitel 2.1.1
[5] Siehe Kapitel 3.5.3.4.4
3.5.3.1 Maßkorrelation
Der am häufigsten verwendete Korrelationskoeffizient ist der die Maßkorrelation beschreibende Pearsonsche Korrelationskoeffizient (Pearsons r). Er wird auch linearer Korrelationskoeffizient genannt.
Voraussetzungen zu seiner Anwendung:
• der Zusammenhang zwischen X und Y ist (annähernd) linear[1],
• beide Variablen sind normalverteilt[2].
Die Berechnung der Maßkorrelation r erfolgt durch folgende Formel:
Verweise:
[1] Siehe Kapitel 3.5.4.2
[2] Siehe Kapitel 3.1.3.1
3.5.3.1.1 Berechnung der Maßkorrelation mit SPSS
Beispiel:
Wir möchten bei Fahrzeugen den Zusammenhang zwischen Gewicht und Beschleunigung feststellen. Wir kontrollieren mithilfe eines Histogramms[1], ob die beiden Variablen annähernd normalverteilt[2] sind:
Kontrolle der ersten Bedingung (Normalverteilung)
Kontrolle der 2. Bedingung (linearer Zusammenhang)
Dann erstellen wir ein Streudiagramm, welches uns einen Einblick gibt, ob die beiden Variablen systematische Entsprechungen zeigen und versuchen, in diese eine Regressionsgerade zu legen[3]. Falls dies möglich ist, ist auch die zweite Bedingung zur Anwendung der Maßkorrelation erfüllt.
Wir sehen einen merkbaren, wenn auch nicht extrem eindeutigen linearen Zusammenhang. Nun haben wir die Voraussetzungen geprüft, um diese Korrelationsberechnung anwenden zu können.
Berechnung der Maßkorrelation mit SPSS:
Klicken Sie in der Menüleiste auf ANAYLISEREN - KORRELATION - BIVARIAT und wählen Sie dort die entsprechende Korrelationsform, nämlich die nach Pearson. Im Feld Variablen fügen Sie die beiden Variablen ein, deren Zusammenhang Sie berechnen möchten. Klicken Sie auf OK:
Ergebnis des Beispiels:
Es gibt einen nachweisbaren Zusammenhang zwischen der Beschleunigung von Fahrzeugen und ihrem Gewicht. Dieser Zusammenhang ist mit einer Irrtumswahrscheinlichkeit von 1 % signifikant[4]. Da es eine negative Korrelation ist, kann man sagen, dass mit steigendem Gewicht des Fahrzeugs seine Beschleunigung abnimmt, was nicht weiter überraschend ist.
Verweise:
[1] Siehe Kapitel 3.6.1.5
[2] Siehe Kapitel 3.1.3.1
[3] Siehe Kapitel 3.5.4.2
[4] Siehe Kapitel 3.5.3.4.4
3.5.3.2 Rangkorrelation R (Krueger-Spearman)
Die Rangkorrelation R (nach Krueger- Spearman) wird v.a. bei der Auswertung psychologischer, pädagogischer und soziologischer Untersuchungen verwendet, wenn also keine wissenschaftlichen Maßeinheiten vorhanden sind, dennoch aber z.B. eine Reihung nach Größe und Intensität sinnvoll sein kann.
Z.B. kann man Kameradschaftlichkeit oder Egoismus kaum sinnvoll in Zahlenwerten messen, aber dennoch Menschen ersuchen, Mitmenschen bezüglich dieser Eigenschaften rangzureihen.
Auch verwendet für Zusammenhänge zwischen metrischen und ordinalskalierten Daten
Man setzt die Rangkorrelation häufig auch ein, wenn man den Zusammenhang von ordinalskalierten[1] und metrischen[2] Variablen berechnen möchte. Dabei wandelt man die Messwerte zuerst in Rangplätze um (nachdem man diese größenmäßig gereiht hat) um danach R berechnen zu können. Fallen mehrere umgewandelte Messwerte auf den gleichen Rangplatz, teilen sie sich diese Plätze (arithmetisches Mittel), also 6., 7., 8. und 9. Platz = 30 (6+7+8+9). 30 dividiert durch 4 (Anzahl der Rangplätze) =7,5. Jeder dieser 4 gleichen Messwerte erhält somit den Rangplatz 7,5.
Berechnung der Rangkorrelation:
R= 1-, di= Differenz des Rangplatzpaares (xi-yi); n= Anzahl der Rangplätze
Beispiel:
Berechnung R= 1-(6*38)/(9*(81-1) = 0,68
Verweise:
[1] Siehe Kapitel 3.1.2.3
[2] Siehe Kapitel 3.1.1.1
3.5.3.2.1 Berechnung der Rangkorrelation mit SPSS
Klicken Sie in der Menüleiste auf ANALYSIEREN - KORRELATION - BIVARIAT und wählen Sie dort die entsprechende Korrelationsform, nämlich die nach Spearman. Im Feld Variablen fügen Sie die beiden Variablen ein, deren Zusammenhang Sie berechnen möchten. Falls die Variablen über höherwertige Skalierungen[1] als die Ordinalskala[2] verfügen (Intervall-[3] oder Proportionalskala[4]), werden sie automatisch von SPSS in die entspechenden Rangplätze umgewandelt. Klicken Sie dann auf OK. Sie erhalten die Ausgabe der Korrelation gemeinsam mit der Beurteilung ihrer Signifikanz[5].
Verweise:
[1] Siehe Kapitel 3.1.2
[2] Siehe Kapitel 3.1.2.3
[3] Siehe Kapitel 3.1.2.4
[4] Siehe Kapitel 3.1.2.5
[5] Siehe Kapitel 3.5.3.4.4
3.5.3.3 Rangkorrelation Tau (Kendall)
Die Rangkorrelation TAU (nach Kendall) wird häufig verwendet, wenn N, also die Gesamtanzahl an Fällen, sehr niedrig ist (< 20).
Berechnung: Zuerst werden alle Ausprägungen der beiden Variablen in Ränge umgewandelt.
Danach wird eine Variable größenmäßig sortiert (nach Rangplätzen), die zum gleichen Fall gehörenden Rangplätze der anderen Variablen werden darunter geschrieben:
Die 1. Rangreihe ist bereits größenmäßig sortiert. In der 2. Rangreihe wird nun verglichen, ob die Rangordnung der 1. Rangreihe (Schulbildung) eingehalten wird. D.h. bei einer maximalen positiven Korrelation von Schulbildung und Schichtzugehörigkeit müsste bei Schichtzubehörigkeit ebenfalls B den 1. Platz haben, E den 2., D den 3. usw., bei einer negativen Korrelation selbstverständlich umgekehrt.
Für jede Person der 2. Rangreihe (Schichtzugehörigkeit) wird nun verglichen, ob auf sie folgenden Rangzahlen größer oder kleiner sind. ’Richtig’ wäre eine größere nach einer kleineren Rangzahl; ’falsch’ eine kleinere nach einer größeren Rangzahl:
Insgesamt überprüfen wir 10 Zahlenpaare. Für jede 'richtige' Zahlenfolge zählen wir ein "Plus", für jede 'falsche' Reihenfolge ein "Minus".
Wir zählen 6-Plus und 4-Minuszeichen, zieht man die Minus von den Plus ab, ergibt sich die Summe S = 2. Diese Summe S wird bei der Berechnung von Tau mit der höchstmöglichen Summe dieser Art Smax verglichen.
Smax errechnet sich aus N(N-1)/2, denn die Gesamtzahl von Paarvergleichen hängt nur von N (also der Länge der Rangreihe ab). Ist die zweite Rangreihe identisch mit der ersten (geordneten), so ergeben sich beim Paarvergleich nur ’richtige’ Reihenfolgen und die Gesamtsumme des "Plus- Zeichen" ist gleich der Summe der insgesamt möglichen Paarvergleiche Smax.
Tau ergibt sich als TAU = S/Smax.
In unserem Beispiel ist Smax = 5*4/2 = 10. TAU ist also gleich 2/10 = 0,2
Diese Berechnungsart sollte nur dann angewendet werden, wenn innerhalb einer Rangreihe keine geteilten Rangplätze auftreten.
3.5.3.3.1 Berechnung von TAU mit SPSS
Klicken Sie in der Menüleiste auf ANAYLISEREN - KORRELATION - BIVARIAT und wählen Sie dort die entsprechende Korrelationsform, nämlich Kendall-Tau. Im Feld Variablen fügen Sie die beiden Variablen ein, deren Zusammenhang Sie berechnen möchten. Falls die Variablen über höherwertige Skalierungen[1] als die Ordinalskala[2] verfügen (Intervall[3] - oder Proportionalskala[4]), werden sie automatisch umgewandelt. Klicken Sie dann auf OK. Sie erhalten die Ausgabe der Korrelation gemeinsam mit der Beurteilung ihrer Signifikanz[5].
Verweise:
[1] Siehe Kapitel 3.1.2
[2] Siehe Kapitel 3.1.2.3
[3] Siehe Kapitel 3.1.2.4
[4] Siehe Kapitel 3.1.2.5
[5] Siehe Kapitel 3.5.3.4.4
3.5.3.4 Aussagekraft einer Korrelation
Die Aussagekraft einer Korrelation hängt von mehreren Faktoren ab:
A. der Höhe der Korrelation
B. der Größe der Stichprobe[1](n)
C. der Sorgfalt beim Ausschluss einer möglichen Scheinkorrelation bzw. des Erkennens verdeckter Korrelationen.
Die statistische Kennzahl der Signifikanz berücksichtigt sowohl die Höhe der Korrelation wie auch die Größe der Stichprobe und gibt Auskunft über die Wahrscheinlichkeit[2], dass die erhaltene Korrelation rein zufällig auftrat. Sie ist statistisch von äußerst großer Bedeutung.
Verweise:
[1] Siehe Kapitel 2.1.1
[2] Siehe Kapitel 1.3.2
3.5.3.4.1 Wann sind Korrelationen bemerkenswert?
Die Größe einer Korrelation sagt alleine noch nichts über ihre Aussagekraft aus. Prinzipiell gilt, dass eine hohe Korrelation umso leichter zu erzielen ist, je kleiner die Stichprobe ausfällt. Bei einer Stichprobengröße von 1 liegt jede Korrelation beim Maximalwert r=1.
Bei kleineren Stichproben (etwa n=20) sind folgende Einschätzungen von r bzw. R weitverbreitet:
Ob eine Korrelation bedeutend oder unbedeutend ist, hängt auch von der Art des (überraschenden) Zusammenhangs ab. Eine hohe Korrelation der Schuhgröße mit der Körpergröße von r=0,8 ist deutlich weniger bedeutend als eine gesicherte Korrelation von r=0,4 bei einer großen Stichprobe über den Zusammenhang zwischen dem Konsum eines bestimmten Nahrungsmittels und der Entwicklung einer bestimmten Krankheit.
3.5.3.4.2 Verdeckte Korrelation
Von einer verdeckten Korrelation spricht man, wenn statistisch keinerlei Korrelation errechnet wurde, obwohl sachlich eindeutig Zusammenhänge vorliegen.
Dies ist z.B. möglich, wenn Subgruppen der untersuchten Population in hohem Maße Tendenzen aufweisen, welche durch andere Subgruppen neutralisiert werden, weil diese sich gegenläufig verhalten.
Fiktives Beispiel: Zusammenhang von Zigarettenkonsum und -werbung
Wir untersuchen, welchen Einfluss ein unterschiedlich intensiver Kontakt mit einer bestimmten Tabak-Werbung auf das Rauchverhalten von Jugendlichen ausübt. Wir stellen fest, dass es keinen messbaren Zusammenhang zwischen dem Konsum der Werbung und dem Zigarettenkonsum gibt. Der Zigarettenkonsum hat sich durch die Wahrnehmung der Werbung nicht verändert.
Ein Blick auf die zugrundeliegenden Daten zeigt jedoch, dass es sehr wohl einen substantiellen Zusammenhang geben muss. Wir betrachten dazu ein Histogramm (In SPSS -> GRAFIKEN - HISTOGRAMM), bei welchem wir die Werbung als Variable eintragen, die Veränderung des Zigarettenkonsums in Felder anordnen als und unter Variable verspachteln das Geschlecht eintragen.
Wir erhalten dann folgende zwei nach Geschlechtern getrennte Histogramme:
Wir sehen, dass bei den Jungen eine perfekte negative Korrelation[1] vorliegt (r=-1), bei den Mädchen hingegen eine perfekte positive Korrelation (r=1). Die Jungen haben die Werbung eher als erschreckend für den Tabakkonsum aufgefasst, die Mädchen hingegen als ermutigend. Am Ende des Untersuchungszeitraums rauchten die Mädchen im gleichen Maße mehr als die Jungen weniger rauchten. Dadurch ergab sich eine Null-Korrelation auf der Ebene der gesamten Stichprobe[2].
Verweise:
[1] Siehe Kapitel 3.5.3
[2] Siehe Kapitel 2.1.1
3.5.3.4.3 Scheinkorrelationen und Störvariable
Eine Scheinkorrelation ist ein statistisch gemessener Zusammenhang zwischen zwei Variablen, welcher nur deshalb auftritt, weil beide Variablen systematisch von einer dritten Variablen beeinflusst werden.
Zusammenhang kann auf Störfaktoren zurückgehen
Die Korrelation ist eine interessante Methode zur Berechnung von Zusammenhängen. Jedoch sollte man sich vergewissern, dass der gemessene Zusammenhang tatsächlich prioritär und somit kausal ist.
Es ist immer auch möglich, dass andere Erklärungen (Störfaktoren) für den Zusammenhang übersehen wurden, was zu Scheinkorrelationen führen kann.
Beispiel 1: Bringen Störche Kinder?
So zeigt sich in Untersuchungen verschiedener Länder ein hoher Zusammenhang zwischen der Storchenpopulation und der Geburtenrate (teilweise bis r=0,7) im Laufe der Jahrzehnte. Die Erklärung dieses verblüffenden Zusammenhanges ist einfach: Durch bessere Bildungs- und Berufschancen der Frauen ging die Geburtenrate zurück, durch zunehmende Umweltbelastung die Storchenpopulation. Daher ist der Zusammenhang von Storchenpopulation und Geburtenrate rein zufällig. Er ergibt sich statistisch einfach dadurch, dass sowohl Storchenpopulation wie auch Geburtenrate hoch mit der Wirtschaftsentwicklung korrelieren. Diese führte zu besseren Jobchancen für Frauen und dadurch auch zu geringeren Kinderzahlen wie auch zu einer zunehmenden Umweltbelastung und damit zu sinkenden Storchenpopulationen.
Beispiel 2: Haben reichere Männer weniger Haare?
Es lässt sich ein hoher Zusammenhang zwischen Männern mit schütterem Haar und hohem Einkommen nachweisen. Tatsächlich besteht aber eher ein Zusammenhang zwischen dem Alter der Männer und ihrem Einkommen und mit zunehmendem Alter nimmt auch die Zahl der Haare ab.
Ist man unsicher, ob eine errechnete Korrelation haltbar ist, kann man kann mögliche Störfaktoren mit der Partiellen Korrelation herausfiltern.
3.5.3.4.3.1 Partielle Korrelation mit SPSS
Beispiel: Korrelation von Fertiliät und weiblicher Lebenserwartung
Wir untersuchen den Zusammenhang zwischen Fertilität und weiblicher Lebenserwartung (basierend auf den Daten in world95.sav der UNO). Eine Rangkorrelation zwischen beiden liefert folgendes Resultat:
Überlegung:
Wir sehen einen hohen und signifikanten Zusammenhang zwischen beiden Variablen. Offensichtlich führt eine große Kinderzahl zu stark abnehmender weiblicher Lebenserwartung und umgekehrt. Doch warum sollte dies so sein? Wir kennen doch Personen in unserer Gesellschaft, welche viele Kinder haben und dennoch in voller Gesundheit sehr alt wurden, während wir auch viele kränkliche einzelstehende Personen kennen. Wir suchen daher nach Variablen, welche die beiden vorhandenen beeinflusst haben könnten und dadurch indirekt deren hohen Zusammenhang begründen. Eine derartige mögliche (Stör-)variable ist die weibliche Alphabetisierungsrate. Sie verbessert den Zugang zu Informationen über verbesserte Gesundheitsvorsorge. Damit erhöht sie die Lebenserwartung. Gleichzeitig bietet sie durch verbesserte Berufschancen in qualifizierteren Bereichen auch häufig bessere Einkommensschancen. Bleibt eine gut verdienende Frau wegen zahlreicher Kinder zuhause, stellt dies gleichzeitig für die Familie einen größeren finanziellen Verlust dar, wie wenn eine schlecht verdienende Frau zuhause bleiben würde. Daher entscheiden sich gebildete Frauen häufig gegen höhere Kinderzahlen. Auch wird die Geburt der ersten Kinder oft hinter den abgeschlossenen Bildungsweg zurückgeschoben, was ebenfalls die Fertilität verringert.
Das waren sachliche Argumente. Die Korrelationen stützen diese Annahme:
Herausrechnung der Störvariable mit SPSS:
Um nun den Einfluss der Störvariable aus der Beziehung weibliche Lebenserwartung/Geburtenrate herauszurechnen, gehen wir in SPSS folgendermaßen vor:
Klicken Sie in der Menüleiste auf ANAYLISEREN - KORRELATION - PARTIELLE KORRELATIONEN.
Im Feld Variablen fügen Sie die beiden Variablen ein, deren Zusammenhang Sie berechnen möchten. Unter Kontrollvariablen fügen Sie die Störvariable ein. Klicken Sie dann auf OK. Sie erhalten die Ausgabe der Korrelation gemeinsam mit der Beurteilung ihrer Signifikanz.
Sie sehen, dass durch den Ausschluss dieser Störvariable die Korrelation zwischen der weiblichen Lebenserwartung und der Fertilität auf die Hälfte gesunken ist.
3.5.3.4.4 Signifikanz der Korrelation
Die Signifikanz ist eine Kennzahl, welche die Wahrscheinlichkeit eines systematischen Zusammenhangs zwischen den Variablen bezeichnet. Sie drückt aus, ob ein scheinbarer Zusammenhang rein zufälliger Natur sein könnte oder mit hoher Wahrscheinlichkeit[1] tatsächlich vorliegt. Man spricht bei der Signikanz von Irrtumswahrscheinlichkeiten oder Signifikanzniveaus. Gängige Formulierungen lauten etwa, dass zwischen den Variablen A und B eine Korrelation von r=0,5 auf dem Signifikanzniveau oder der Irrtumswahrscheinlichkeit von p ≤ 1 % besteht. Dies bedeutet, dass die zwischen den Variablen A und B gefundene Korrelation in dieser Höhe und bei dieser Stichprobengröße nur in weniger als 1 % aller Fälle rein zufällig auftritt.
Die Kennzahl p der Irrtumswahrscheinlichkeit, auf deren komplexe Berechnung hier nicht eingegangen wird, berücksichtigt somit sowohl die Höhe der Korrelation wie auch die Größe der Stichprobe. Ist die Stichprobe[2] sehr klein, muss die Korrelation extrem groß ausfallen, um signifikant sein zu können. Hingegen kann auch eine Korrelation von r=0,2 bei sehr großen Stichproben signifikant werden.
Grenzwerte der Signifikanz bei n=20
Für eine Stichprobe der Größe n = 20 finden wir für einseitige Irrtumswahrscheinlichkeit (Signifikanz) folgende Grenzwerte:
Irrtumswahrscheinlichkeit p ≤ 5 %: r/R/TAU muss größer sein als 0,377
Irrtumswahrscheinlichkeit p ≤ 1 %: r/R/TAU muss größer sein als 0,534
D.h. wenn man eine Korrelation von 0,6 bei einer Stichprobe von n=20 ermittelt, dann ist die Wahrscheinlichkeit geringer als 1 %, dass dieser Zusammenhang rein zufälliger Natur ist.
Bestimmtheitsmaß: Anteil der Korrelation an Veränderung
Wenn der Korrelationskoeffizient quadriert wird, erhält man das Bestimmtheitsmaß (R2), den Anteil der durch eine Variable erklärten Streuung an der Streuung der anderen. R/r=0,8 bedeutet nicht, dass 80 % der Stichprobe einander entsprechen. R2 gibt Aufschluss darüber, dass 0,8*0,8=0,64 = 64 % der Variabilität der Werte beider Variablen durch den Zusammenhang bestimmt sind.
Verweise:
[1] Siehe Kapitel 1.3.2
[2] Siehe Kapitel 2.1.1
3.5.3.4.4.1 Signifikanz mit SPSS
Signifkanz von Korrelationen wird von SPSS automatisch ermittelt
Statistikprogramme wie SPSS ermitteln selbstständig bei der Berechnung der Korrelation die dazugehörige Irrtumswahrscheinlichkeit. Bei SPSS wird mit Sternen ausgedrückt (1, 2 oder 3 Sterne), ob die Korrelation signifikant ist, d.h. ob der Zusammenhang weitgehend gesichert scheint oder nicht.
Drei wesentliche Schwellen der Irrtumswahrscheinlichkeit[1] haben breite Akzeptanz gefunden:
- p <= 0,05 (die Wahrscheinlichkeit einer rein zufälligen Korrelation liegt bei unter 5 %, SPSS vergibt einen Stern = *);
- p <= 0,01 (die Irrtumswahrscheinlichkeit ist kleiner als 1 %, SPSS vergibt 2 Sterne **) oder
- p <= 0,001 (die Irrtumswahrscheinlichkeit ist kleiner als 1 ‰, SPSS vergibt 3 Sterne ***).
Diese Korrelation zeigt, basierend auf UNO- Statistiken aus dem Jahr 1995, den Zusammenhang zwischen der täglichen Kalorienaufnahme und dem Bruttonationalprodukt von Ländern. Defaultmäßig berechnet SPSS zur Korrelation auch die Signifikanz der Korrelation und markiert signifikante Korrelationen wie in diesem Beispiel mit Sternchen. Diese Korrelation ist signifikant auf dem 1%-Niveau (2 Sternchen). Damit signifikante Korrelationen automatisch mit Sternchen markiert werden, muss im Fenster der Korrelationsberechnung der Punkt signifikante Korrelationen markieren mit einem Häkchen markiert sein.
Verweise:
[1] Siehe Kapitel 1.3.2
3.5.3.5 Kovarianz
Die Kovarianz ist eine Kennzahl für den Zusammenhang von zwei Variablen. Sie entspricht der Summe der gemittelten Abweichungsprodukte der Variablen. Sie wird nach folgender Formel berechnet:
Die Kovarianz ist positiv, wenn X und Y tendenziell einen linearen Zusammenhang besitzen, d. h. hohe Werte von X entsprechen hohen Werten von Y und niedrige Werte von X niedrigen Werten von Y.
Die Kovarianz ist negativ, wenn X und Y einen gegensinnigen linearen Zusammenhang aufweisen, d. h. hohe Werte von X gehen einher mit niedrigen Werten von Y und umgekehrt.
Da die Kovarianz in ihrer Rohform von der Größe der zugrundeliegenden Daten abhängt, ist die Einschätzung ihres Wertes ohne die Kenntnis der zugrundeliegenden Daten nicht einschätzbar. Dazu muss sie erst standardisiert werden, was zur Korrelation[1] führt.
Verweise:
[1] Siehe Kapitel 3.5.3
3.5.4 Regression
Die Regression(sanalyse) ist ein Verfahren zur Analyse von Beziehungen zwischen einer abhängigen und einer oder mehreren unabhängigen Variablen. Während die Korrelation[1] die Stärke eines Zusammenhangs zeigt, erlaubt es die Regression, von einer bekannten Größe einer Variable auf die vermutliche Größe der abhängigen Variablen zu schließen, falls ein systematischer Zusammenhang zwischen zwei Variablen A und B vorliegt.
Prinzipiell unterscheidet man zwischen linearer und nicht-linearer Regression.
Bei der linearen Regression kann eine Art Regressionsgerade ins Histogramm gelegt werden, welche die Möglichkeit der annähernden Voraussage von Ausprägungen bietet.
Der Verlauf der Regressionsgerade wird über die Formel
y = b*x + a
ermittelt, wobei b den Regressionskoeffizienten darstellt, welcher den Tangens des Steigungswinkels der Regressionsgeraden angibt. Der Regressionskoeffizient wird über die nachfolgende Formel ermittelt:
Verweise:
[1] Siehe Kapitel 3.5.3
3.5.4.1 Statistisch-mathematische Berechnung der linearen Regression
Die lineare Regression kann mit SPSS auf folgende Weise ermittelt werden:
A. Klicken Sie auf ANALYSIEREN - REGRESSION - LINEAR. Es erscheint folgendes Fenster:
B. Tragen Sie in Abhängige Variable die von Ihnen gewünschte metrische Variable ein; in unabhängige Variable diejenige Variable, deren Einfluss auf die erste Variable Sie ergründen möchten.
C. Klicken Sie auf OK. Sie erhalten nun folgende Ausgaben:
Erklärungen:
Was in der ersten Tabelle R genannt wird, ist die Quadratwurzel aus dem Bestimmtheitsmaß und deckt sich bei der einfachen Regressionsanalyse mit dem Korrelationskoeffizienten[1] von Pearson. Die Korrelation von 0,711 ist durchaus ansehnlich.
Unter Koeffizienten stehen die zwei wesentlichen Werte für die Berechnung der Regressionsgerade: Die Konstante (hier 127,203) ist der Ausgangswert, der darunter stehende Wert -1,129 der Multiplikationsfaktor.
Die hier vorliegende Gleichung, die wir errechnen wollten, ist also:
A = -1,129*B + 127,203 oder in konkreten Begriffen formuliert:
Kindersterblichkeit (pro Tausend) = (weibliche Alphabetisierungsrate)*(-1,129) + 127,203
Bei einer weiblichen Alphabetisierungsrate von 50 % könnte man somit eine Kindersterblichratsrate von -1,129*50 + 127,203 voraussagen, also 70,753.
Es sei hinzugefügt, dass es sich hier nur um eine Einführung in die Regressionsanalyse handelt und deshalb auf wichtige damit zusammen hängende Begriffe wie Standardfehler der Schätzung nicht eingegangen werden kann.
Verweise:
[1] Siehe Kapitel 3.5.3.1
3.5.4.2 Grafische Darstellung der Regression
Grafisch kann man eine Regressionsgerade mit SPSS auf folgende Weise erstellen: Klicken Sie in der Menüleiste auf GRAFIKEN - STREU- /PUNKTDIAGRAMM - EINFACHES STREUDIAGRAMM. Dort geben Sie nach Klick auf Definieren in der Y- Achse eine metrische Variable ein, in der X-Achse genauso. Dann klicken Sie auf OK. Sie erhalten zuerst ein Streudiagramm, vorerst noch ohne Regressionsgerade:
Nun machen Sie einen Doppelklick auf das Diagramm in der SPSS- Ausgabe. Sie landen im Diagramm-Editor. Unter Elemente können Sie Anpassungslinie bei Gesamtwert anklicken. Daraufhin wird defaultmäßig eine Regressionsgerade in das Streudiagramm eingefügt, gleichzeitig öffnet sich das folgende Fenster:
Kontrollieren Sie nochmals, ob hier Linear angeklickt ist. Nur linear realisiert eine Regressionsgerade. Nach Zuweisen erhalten Sie nun das Streudiagramm[1] mit der entsprechenden Regressionsgerade:
Verweise:
[1] Siehe Kapitel 3.6.1.6
3.6 Die grafische Darstellung statistischer Ergebnisse
Ein Bild sagt mehr als 1000 Worte
Dies trifft auch für die Statistik zu. Wer es versteht, mit einfachen, klaren und aussagekräftigen Diagrammen zu punkten, wird für eine leichten und einprägsamen Zugang zu seinen Analysen Anerkennung finden.
Vorteil von Diagrammen liegt in Einfachheit der Darstellung
Allzuleicht lässt man sich von der Vielfalt an grafischen Darstellungsmöglichkeiten beeinflussen und meint, Diagramme noch ein wenig optisch ausgefaller, dreidimensional, vermeintlich attraktiver mit zahlreichen Schmankerln machen zu müssen, bis irgendwann einmal der Vorteil eines Diagramms gegenüber einer komplexen Tabelle verloren geht und die BetrachterInnen ratlos vor einem schwierig zu deutenden Kunstwerk sitzen. Niemand ist bereit, einige Minuten vor einem komplexen Diagramm zu sitzen, um zu versuchen, es zu verstehen. Mit Diagrammen gewinnt man die BetrachterIn in wenigen Sekunden oder man verliert sie/ihn. Die Notwendigkeit der inhaltlichen Klarheit und dadurch Schlichtheit eines Diagramms hat klare Priorität vor der künstlerischen Gestaltung.
Nicht jedes Diagramm ist für jede Datenlage geeignet.
Man sollte bedenken, dass nicht jedes Diagramm für jede Art von Information geeignet ist. Manche Diagramme, wie Kreisdiagramme[1], werden von den BetrachterInnen mit einem Ganzen, also 100 % assoziiert, und würden bei der Wiedergabe von Mehrfachantworten[2] zu falschen Schlüssen führen.
Begleitinformationen sind wichtig
Auch Diagramme benötigen Begleitinformationen, um sie voll verständlich zu machen und wissenschaftliche Seriösität nachzuweisen.
Was in Diagrammen, was im Text?
Zeigen Sie mit Diagrammen besondere Eigenheiten der Daten und packen Sie die Analysen und anderen notwendigen Begleitinformationen in den Text.
Verweise:
[1] Siehe Kapitel 3.6.1.1
[2] Siehe Kapitel 3.2.2
3.6.1 Arten von Diagrammen
Wesentliche Diagrammformen sind:
- Balkendiagramme, inklusive gruppierten Diagrammen und Stapelbalkendiagrammen
- Liniendiagramme
- Flächendiagramme
- Kreisdiagramme
- Boxplots[1]
- Streudiagramme
- Histogramme
- Kartogramme
Viele Programme ermöglichen die Erstellung von Diagrammen
Mit Ausnahme von Boxplots und Kartogrammen können alle Diagrammformen von den gängigen Programmen erstellt werden, wie sogar von WinWord (EINFÜGEN - GRAFIK - DIAGRAMM) oder Excel. In SPSS geht man in der Menüleiste zu GRAFIKEN und findet dort alle hier angeführten Diagrammformen und viele mehr zur Auswahl.
Auch hier gilt, dass professionelle statistische Programme wie z.B. SPSS oder Statistica Vorteile aufweisen, da sie eine Fülle feiner Einstellungen erlauben, welche mit Bordmitteln nicht zu erreichen sind. Auch verbinden sie in effizienter Form im gleichen Menüpunkt die gleichzeitige Berechnung und Erstellung komplexer Statistiken wie auch von Diagrammen.
Verweise:
[1] Siehe Kapitel 3.4.5.1
3.6.1.1 Kreisdiagramme
Kreisdiagramme (auch Tortendiagramme) genannt, sind eine beliebte grafische Darstellungsform, um die Aufteilung eines Ganzen aufzuzeigen.
Für die grafische Darstellung kategorieller Daten (Nominal[1]- oder Ordinalskalen[2]) verwendet man Diagrammformen, die eine möglichst klare Darstellung der relativen Anteile erlauben. Alle Anteile müssen zusammen 100 % ergeben. Der relative Anteil der einzelnen Bestandteile soll sofort optisch erkennbar sein. Damit diese relativen Anteile auf einem Blick größenmäßig eingeordnet werden können, dürfen nicht zu viele Kategorien verwendet werden. Sind sie zu zahlreich, sollten kleinere Kategorien nach Möglichkeit zusammengefasst werden. Andernfalls ist die Darstellung in Form einer Tabelle besser geeignet.
Besonders gut geeignet für die Darstellung relativer Anteile sind Torten- oder Kreisdiagramme:
Optimal große Teile, aber nicht zu viele.
Für das menschliche Auge sind Winkel von mehr als 90 Grad besonders gut zu erkennen. Deshalb eignen sich Tortendiagramme besonders zur Darstellung von Mehrheiten oder von Anteilen von mindestens einem Viertel.
Wird die Anzahl der Anteile und damit der Tortenstücke zu zahlreich, wird ein Tortendiagramm schnell unübersichtlich, besonders wenn gleichzeitig seine größten Stücke kleiner als ein Viertel werden:
Hier ist es nur mehr mit Mühe möglich, die Tortenstücke nach ihrer Größe zu reihen, da die Rundung die Abschätzung der relativen Größe erschwert. Daher wären für die Darstellung vieler Subeinheiten eines Ganzen Stapelbalkendiagramme[3] besser geeignet.
Keinesfalls für Mehrfachantworten
Gänzlich ungeeignet sind Kreisdiagramme, um die Ergebnisse von Fragen mit Mehrfachantworten darzustellen:
Bei Kreisdiagrammen neigen BetrachterInnen dazu, die gesamte Torte als etwas Ganzes, also als 100 % aufzufasssen.Da bei Mehrfachantworten jedoch mehr als 100 % auftreten können (auch weniger als 100 %), kann dies zu einer falschen Interpretation führen. Deutlich besser wären für diesen Zweck horizontale Balkendiagramme geeignet.
Verweise:
[1] Siehe Kapitel 3.1.2.2
[2] Siehe Kapitel 3.1.2.3
[3] Siehe Kapitel 3.6.1.3
3.6.1.2 Liniendiagramme
Liniendiagramme eignen sich besonders für die Darstellung von Entwicklungen, ganz besonders auch, wenn komparativ die Entwicklung von zwei oder mehr Populationen[1] miteinander verglichen wird. Durch die feinen Striche kann man auf engstem Raum Informationen gleich zu mehreren Untersuchungsobjekten unterbringen, wie man im folgenden fiktiven Beispiel sieht, in welchem gezeigt wird, wie sich in verschiedenen Ländern die Akzeptanz der Aufnahme eines weiteren Landes in die Europäische Union veränderte.
Man sieht auf einem Blick, dass in Schweden die Akzeptanz von einem hohen Niveau ausgehend stark zurückging, in Irland eher gering blieb, sich in Polen hingegen von einem sehr geringem zu einem relativ hohen Niveau entwickelte.
Verweise:
[1] Siehe Kapitel 2.1
3.6.1.3 Balkendiagramme
Einfache Balkendiagramme sind, da sie vom gleichen Nullpunkt ausgehen, sehr gut geeignet, um komparativ auch kleinste Unterschiede zwischen Subbereichen erkennbar zu machen.
Sie sind die beste Darstellungsform, um z.B. die Ergebnisse von Fragen mit Mehrfachantworten zu präsentieren.
Balkendiagramme können sowohl horizontal (wie das obige Beispiel) wie auch vertikal orientiert sein.
Das gruppierte Balkendiagramm
Dieses ist besonders geeignet für die kontrastive Darstellung der Ausprägungen einer Variable (z.B. männlich-weiblich für Geschlecht, Hinduismus-Islam etc. für Religionen). So kann man z.B. vergleichend zeigen, wie Männer und Frauen in verschiedenen Bereichen abschneiden. Siehe ein Beispiel dazu bei der Berechnung mit SPSS.
Stapelbalkendiagramme: Anteile vom Ganzen
Stapelbalkendiagramme werden - neben Kreisdiagrammen - oft verwendet, um Anteile am Ganzen darzustellen. Zur Darstellung von relativen Mehrheiten sind sie etwas weniger übersichtlich als Kreisdiagramme.
Auch sie werden sehr schnell unübersichtlich, wenn die Kategorien zu zahlreich werden, bleiben bei einer größeren Zahl von Subeinheiten aber noch übersichtlicher als Kreisdiagramme:
Vergleich der Aufteilung: Stapelbalkendiagramme
Gestapelte Balkendiagramme sind besonders wertvoll beim Vergleich der Aufteilung der gleichen Variable in verschiedenen Stichproben/Populationen[1].
Verweise:
[1] Siehe Kapitel 2.1
3.6.1.3.1 Gruppierte Balkendiagramme mit SPSS
Im folgenden Diagramm interessiert uns, inwieweit sich die männliche und die weibliche Lebenserwartung in den Ländern dieser Welt nach deren religiöser Ausrichtung unterscheiden. Wir greifen dabei auf Daten in world95.sav bei der Berechnung mit SPSS zurück. Der Vorgang mit SPSS erfolgt folgendermaßen:
A. Klicken Sie auf GRAFIKEN - BALKEN
B. Wählen Sie das Symbol für Gruppiert und dann Auswertung über verschiedene Variablen.
C. Nun wählen wir zumindest zwei numerische Variablen aus (welche wir vergleichend zu den Religionen betrachten wollen, in unserem Falle die männliche und die weibliche Lebenserwartung). Diese schieben wir in das Feld Bedeutung der Balken:
D. Im Feld Kategorienachse fügen wir die Kategorienvariable (in unserem Falle die dominierende Religion des Landes) ein.
E. Bei Klick auf Auswertungsfunktion können wir uns für bestimmte Kennzahlen entscheiden, wie den Median[1], das arithmetische Mittel[2], die Häufigkeit[3], Summe, welche für die numerischen Variablen berechnet werden..
Nach Klick auf OK erhalten wir das folgende Diagramm:
Verweise:
[1] Siehe Kapitel 3.3.3
[2] Siehe Kapitel 3.3.2
[3] Siehe Kapitel 3.2.2
3.6.1.4 Kartogramme
Kartogramme sind eine Sonderform von Diagrammen und zeigen die Ausprägungen einer Variable auf Landkarten.
Kartogramme sind meist nur mit relativ teuren Programmen möglich, wie z.B. Arcview. Zu Excel gibt es eine billigere Zusatzsoftware wie Mapland (99-999 $). MS Office 2000 Professional enthielt noch eine vereinfachte Excel-Komponente namens Microsoft Map.
Kartogramme in Wahlanalysen häufig
Mittels Kartogrammen können v.a. regional unterschiedliche Ausprägungen sehr gut wiedergegeben werden. Sie werden z.B. bei der TV-Berichterstattung an Wahlabenden eingesetzt, um unterschiedliche Wahlpräferenzen in den verschiedenen Bundesländern und Regionen aufzuzeigen.
3.6.1.5 Histogramme
Unter einem Histogramm versteht man die grafische Darstellung der Häufigkeitsverteilung[1] von Messwerten.
Die Daten sind dabei größenmäßig auf der X-Achse geordnet, während auf der Y- Achse ihre Häufigkeiten stehen. Über jeder Klasse wird ein Rechteck errichtet, dessen Fläche proportional zur klassenspezifischen Häufigkeit ist.
Histogramme werden besonders zur Darstellung von Verteilungen verwendet, wie auch zur Demonstration der Normalverteilung[2].
Verweise:
[1] Siehe Kapitel 3.1.3.3.2
[2] Siehe Kapitel 3.1.3.3.1
3.6.1.6 Streudiagramme
Streudiagramme (oder Punktdiagramme) ermöglichen die grafische Darstellung des Zusammenhangs von zwei Variablen.
Die Ausprägung der Variable A wird auf der X- Achse eingetragen, die Ausprägung der Variable B auf der Y-Achse.
Basierend auf UN-Daten über die Entwicklung der Länder dieser Welt (siehe world95.sav) zeigt dieses Diagramm den Zusammenhang zwischen Kindersterblichkeit und weiblicher Alphabetisierung. Man sieht deutlich, dass mit steigender Alphabetisierungsrate der Frauen die Kindersterblichkeit drastisch zurückgeht. Streudiagramme eignen sich vorzüglich zum Aufzeigen des Zusammenhangs zwischen Variablen[1] und somit auch zur Darstellung der Regression und der Korrelation[2].
Verweise:
[1] Siehe Kapitel 3.5.1
[2] Siehe Kapitel 3.5.4.2
3.6.2 Welches Diagramm für welche Daten?
3.6.3 Notwendige Begleitinformationen von Diagrammen
Diagramme brauchen Begleitinformationen
Diagramme sollten genauso wie die tabellarische Darstellung statistischer Daten alle notwendigen Begleitinformationen aufweisen, die zum Verständnis des Diagramms sowie zum Nachweis der Seriösität der Arbeit wichtig sind. Dazu zählen:
A. Name des Erstellers, v.a. wenn es sich um Fremddiagramme handelt;
B. Falls es sich nicht um eigene Daten handelt, auf deren Grundlage das Diagramm erstellt wurde, sollte die Quelle der Daten angegeben werden (z.B. Statistikamt der Stadt Ulm 1997) (am besten unterhalb des Diagramms)
C. Jahr der Erhebung der Daten;
D. Größe der Stichprobe (am Besten die bereinigte Größe, welche Null-Eingaben und fehlerhafte Eingaben nicht berücksichtigt), v.a. wenn es sich um eigene Daten handelt. Bei gut bekannten Fremddatenquellen wird darauf meist verzichtet (z.B. bei Erhebungen statistischer Zentralämter etc.)
E. Angabe der Messeinheiten (cm, Zähleinheiten, Prozent etc.)
F. Aussagekräftiger Titel des Diagramms (ganz oben)
G. Aussagekräftige Bezeichnungen für die Bestandteile des Diagramms (z.B. für Daten auf der x- bzw. y-Achse.
H. Eventuell Hinweis auf Art der Erhebung der Daten
I. Bei Mehrfachantworten unbedingt Hinweis darauf
Das folgende Diagramm (Quelle: http://www.mzes.uni-mannheim.de/publications/wp/wp-89.pdf[1]) berücksichtigt diese Erfordernisse. Obwohl gleichzeitig viele Daten dargestellt werden müssen, bleibt der Erkenntnisgrad hoch.
Verweise:
[1] http://www.mzes.uni-mannheim.de/publications/wp/wp-89.pdf
4. Software für quantitative Forschungsprojekte
Für zuhause Excel, an der Universität SPSS
Nur wenige Menschen verfügen auf dem eigenen PC über spezifische Statistiksoftware. Viele Berechnungen und grafische Darstellungen lassen sich jedoch auch mit gängigen Software-Programmen erstellen.
Besonders die Tabellenkalkulation Microsoft Excel (aber praktisch auch jede andere Tabellenkalkulation vergleichbarer Qualität) verfügt über eine Fülle statistischer Funktionen, mit welchen auch recht ausgefeilte statistische Analysen erledigt werden können und auch über zahlreiche Möglichkeiten, die Ergebnisse mit anschaulichen Diagrammen[1] darzustellen.
Wer jedoch sehr viel mit Statistiken zu tun hat und leichten Zugang zu Software wie SPSS hat, welches auch auf den PCs im PC-Raum des Instituts für Kultur- und Sozialanthropologie zu finden ist, wird den leichten Wechsel zu diesem Programm nicht bereuen (zu finden unter Start - Programme - SPSS für Windwows). Daten von Standard-Programmen wie Excel können leicht übernommen werden, statistische Berechnungen können sehr komfortabel in jeder beliebigen Tiefe getätigt werden. Wer ein wenig eingearbeitet ist, kann mit Programmen wie SPSS viele Analysen um ein Vielfaches schneller als mit Excel abschließen.
Verweise:
[1] Siehe Kapitel 3.6
4.1 Was kann Excel?
Excel gut geeignet für einfache Berechnungen und schöne Diagramme
Excel ist als Teil des Programms Microsoft Office fast auf jedem PC vorhanden. Bereits mit Excel kann man, wenn auch nicht so komfortabel wie mit SPSS, viele statistische Verfahren durchrechnen und auch grafisch darstellen.
Übernahme von Excel in SPSS problemlos möglich
Da Excel auf fast jedem PC vorhanden ist, eignet es sich sehr gut dazu, Daten zu sammeln und erste Voranalysen mit einfachen statistischen Methoden zu machen. Da sowohl Excel wie auch SPSS ein Datenblatt (Tabelle) zur Verwaltung der Daten verwenden, ist die Übernahme von Daten aus Excel ins SPSS ausgesprochen einfach.
4.1.1 Statistische Analysen mit Excel
Excel bietet u.a. folgende statistische Analyse-Methoden an:
- Chi-Quadrat-Test
- Häufigkeit
- Korrelation
- Kovarianz
- Median
- Mittelwert
- Modalwert
- Quartile
- Rangkorrelation
- Maßkorrelation
- Standardabweichung
- Varianz
- T-Test usw.
Der Ablauf von Berechnungen mit Excel:
A. Setzen Sie den Cursor in eine freie Zelle, in welcher das Berechnungsergebnis landen soll
B. Klicken Sie in der Menüleiste zuerst auf EINFÜGEN und dann auf das Untermenü FUNKTION.
C. Wählen Sie in KATEGORIE AUSWÄHLEN den Subbereich STATISTIK aus.
D. Wählen Sie nun die gewünschte statistische Funktion.
E. Machen Sie einen Doppelklick auf die Funktion, Sie werden nun nach den Funktionsargumenten gefragt (d.h. nach den Zahlenwerten, die Sie analysieren möchten).
F. Markieren Sie nun mit der Maus (linke Maustaste dabei festhalten) den von Ihnen gewünschten Zahlenblock (also z.B. B2 bis B75).
G. Drücken Sie die Returntaste und das Ergebnis sollte im vorher freien Feld landen.
Sollten Sie, wie z.B. bei der Korrelation zwei Argumente eingeben müssen, dann müssen Sie den Punkt F zweimal wiederholen. Beim ersten Mal geben Sie den Cursor in die erste Zeile des Fensters (bei der Korrelation Matrix1 genannt) und markieren mit der Maus die erste Datenspalte (z.B. Körpergröße); dann setzen Sie den Cursor in das Feld Matrix2 und markieren mit der Maus die zweite von Ihnen gewünschte Datenspalte (z.B. Schuhgröße). Wenn Sie nun auf OK klicken, wird die Korrelation zwischen Körper- und Schuhgröße berechnet und in das freie Feld eingetragen.
4.1.2 Grafische Aufbereitung von Daten mit Excel
Viele statistische Funktionen
Excel hat eine sehr leistungsfähige und einfache Funktion für die Herstellung ansehnlicher statistischer Grafiken.
Excel bietet u.a. folgende statistische Grafiken (Diagramme) an:
- Säulen
- Balken
- Linien
- Kreis
- Fläche
- Ring
- Histogramm (bei Installation eines mitgelieferten Add-Ins, siehe Online-Hilfe bei Microsoft Office 2003)
- Netz usw.
Die Erstellung von Diagrammen mit Excel:
Sie ist extrem einfach:
A. Markieren Sie die Zahlenreihen, welche Sie grafisch darstellen möchten.
B. Klicken Sie in der Menüleiste auf EINFÜGEN und danach auf DIAGRAMM.
C. Ihre Zahlenreihen wurden damit schon automatisch übernommen und Sie können jetzt das Diagramm feinjustieren (Titel, Diagrammart, Größe, Farben etc.)
4.2 Was kann MS Access?
Gut zum Sammeln von Daten, wenige Analysemöglichkeiten
Microsoft Access kann, da seine Daten ebenfalls in Form einer Tabelle verwaltet werden, sehr gut zum Sammeln der Daten verwendet werden. Seine Analysemöglichkeiten sind jedoch, abgesehen von einer sehr guten Kreuztabellenfunktion (zu finden unter Abfragen) eher beschränkt.
4.3 Profi-Programme: SPSS und Statistica
Komfort, Schnelligkeit und großer Funktionsumfang: die Profiprogramme
Profiprogramme wie SPSS oder Statistica weisen eine enorme Vielfalt statistischer Funktionen auf, deutlich mehr als Excel oder MS Access. Da SPSS auf allen PCs an der KSA installiert ist, wird in diesem Online-Kurs die Umsetzung statistischer Analysen und Darstellungen mit SPSS in vielen Bereichen angeboten. Statistica ist ebenfall eine exzellente Software, deren Bedienung auf der vorliegenden Homepage jedoch nicht demonstriert werden kann.
4.4 Datentransfer zwischen Programmen: Von Excel und Access zu SPSS
Leichter Datentransfer zwischen Excel bzw. Access und SPSS
Der Datentransfer zwischen diesen Programmen ist ausgesprochen einfach:
A. Speichern Sie die gewünschten Daten, ob in Excel oder in Access, jeweils als Excel- Dokument ab: Gehen Sie zu DATEI - SPEICHERN UNTER und klicken Sie nun MICROSOFT OFFICE EXCEL- ARBEITSMAPPE (*.xls) an.
B. Schließen Sie Excel oder Access
C. Öffnen Sie das Programm SPSS
D. Gehen Sie zu DATEI - DATEI ÖFFNEN
E. Standardmäßig wird als Dateityp natürlich der SPSS- Dateityp *.SAV angezeigt, daher können Sie vorerst die abgespeicherte Excel-Datei noch nicht sehen. Wählen Sie daher im Auswahlfenster unter Dateityp Excel (Endung *.xls) und bestätigen Sie mit einem Häkchen, dass die Variablennamen eingelesen werden sollen (andernfalls werden diese nicht in gewünschter Weise übernommen).
F. Klicken Sie auf OK, die Datei wird nun eingefügt. Falls Sie Variablennamen verwendeten, welche länger als acht Zeichen waren, werde diese auf acht Zeichen verkürzt und Sie erhalten eine Information von SPSS darüber.
G. Speichern Sie nun die Datei unter einem beliebigen Namen in SPSS (die Endung *.SAV wird automatisch angenommen).
4.5 Umcodierung
Einfache Transformation von Daten mit SPSS
SPSS benötigt zur internen Berechnung mitunter andere Datenarten (v.a. numerische), als sie von anderen Programmen, auch WinWord überliefert werden. SPSS bietet sehr komfortable Möglichkeiten der automatischen Umwandlung[1] von Daten, sowie auch ihrer automatischen Rückwandlung[2] für die Bildschirm- und Druckausgabe.
Verweise:
[1] Siehe Kapitel 2.2.3.2
[2] Siehe Kapitel 2.2.3.3
5. Lexikon statistischer Grundbegriffe
Hier finden Sie die wichtigsten statistischen Grundbegriffe alphabetisch geordnet.
5.1 A-C
Abhängige Variable
Darunter versteht man Variable, deren Ausprägung durch eine oder mehrere andere Variablen systematisch beeinflusst werden. So wäre z.B. in der Landwirtschaft der Ernteertrag abhängig z.B. von der Bodenqualität wie auch vom Einsatz von Düngemitteln.
Alpha-Fehler
Siehe Fehler der 1. Art
Alternativhypothese
Unter einer Alternativhypothese versteht man bei statistischen Tests die Gegenhypothese H1 zur Nullhypothese H0. Vor Durchführung von Tests legt man Annahmen über die Grundgesamtheit fest, welche mit Tests überprüft werden.
Analytische Statistik (auch Schließende Statistik oder Inferenzstatistik)
Mithilfe von Verfahren der analytischen Statistik versucht man, von Stichproben auf die Grundpopulation bei Berücksichtigung unterschiedlicher Wahrscheinlichkeiten zu schließen. Dazu kommen eine Vielzahl weiterer weiterführender Verfahren wie Clusteranalyse, Faktorenanlyse multivariate Verfahren,... Siehe auch: Induktive Statistik (Wikipedia)[1].
Arbeitshypothese
Darunter versteht man eine genau festzulegende Annahme, von der man zu Beginn eines Forschungsprojektes ausgeht. Siehe auch Nullhypothese.
Arithmetisches Mittel (oder Durchschnitt/-swert)
Das am häufigsten verwendete Lagemaß, welches den Durchschnittswert (Summe aller Werte dividiert durch ihre Anzahl) einer Variablen zeigt. Es sollte nur bei metrischen Variablen eingesetzt werden.
Ausprägungen
Unter Ausprägungen versteht man die Gesamtheit der möglichen Werte eines Merkmals.So kann z.B. die Variable Geschlecht die Ausprägungen männlich und weiblich annehmen.
Ausreißer
Darunter versteht man einen extrem großen oder extrem kleinen Wert, welcher weit von den restlichen Einträgen entfernt ist. Dies könnte z.B. der Fall beim Einkommen eines Millionärs sein, welcher in einem sehr armen Dorf lebt.
Balkendiagramm (auch Säulen- oder Blockdiagramm)
Dabei handelt es sich um Diagramme, bei welchen die Größe der Werte mit der Länge von Balken bzw. Säulen ausgedrückt werden. Werden die Werte (oft Häufigkeiten) senkrecht aufgetragen, spricht man in engerer Terminologie von Säulendiagrammen, werden sie waagrecht aufgetragen, von Balkendiagrammen.
Bestimmtheitsmaß (auch Determinationskoeffizient)
Das Bestimmtheitsmaß ist ein Maß für den Zusammenhang zwischen zwei Variablen und entspricht dem Quadrat des Korrelationskoeffizienten r. Es gibt an, in welchem Ausmaß die Varianz der einen Variablen durch die Varianz der anderen Variablen bestimmt wird. Siehe auch: Bestimmtheitsmaß (Wikipedia)[2].
Beta-Fehler
Siehe Fehler der 1. und 2. Art.
bimodal
Darunter versteht man das Auftreten von zwei Gipfeln in einer Häufigkeitsverteilung, d.h. von zwei Modalwerten.
Biseriale Korrelation
Die biseriale Korrelation rbis zeigt den Zusammenhang von zwei metrischen und normalverteiltenVariablen, von denen eine künstlich dichotomisiert wurde (in zwei Gruppen unterteilt).
bivariat
Bivariat bezeichnet, dass von den Betrachtungen gleichzeitig zwei Variablen betroffen sind. Siehe z.B. die bivariate Häufigkeitsverteilung[3].
Blockbildung
Unter Blockbildung, auch Clusterbildung genannt, versteht man die Zusammenfassung von Elementen der Untersuchung, welche wesentliche für die Untersuchung relevante Eigenschaften gemeinsam haben, zu Blöcken oder Clustern. SPSS ermöglicht es, derartige Cluster mithilfe der Clusteranalyse zu ermitteln. Der Vorteil der Clusterbildung liegt darin, dass durch die Schaffung größerer Einheiten sinkt auch die Fehlerwahrscheinlichkeit von Aussagen. Siehe zur Clusteranalyse: Clusteranalyse (Wikipedia)[4].
Blockdiagramm
Siehe Balkendiagramm[5].
Boxplot
Unter Boxplots versteht man eine graphische Darstellung der Lage und der Verteilung stetiger Merkmale beruhend auf den empirischen Quartilen. Der Abstand zwischen dem 1. und dem 3. Quartil wird als ein Rechteck dargestellt, in welchem durch einen waagrechten Strich auch der Median verzeichnet ist. Siehe wegen weiterer Eigenheiten dazu auch: Vergleichende grafische Darstellung[6] von Streuung und Lage mit Box-Plots.
Chi-Quadrat-Test
Der Chi-Quadrat-Test ist ein statistisches Verfahren, um die Unabhängigkeit von zwei Merkmalen zu überprüfen. Er wird besonders gerne bei der Kreuztabellen-Analyse[7] eingesetzt. Siehe dazu auch: Chi-Quadrat-Test (Wikipedia)[8].
Clusterbildung
siehe Blockbildung
Codeplan
Darunter versteht man die schriftliche Zusammenfassung der Umsetzung der erhobenen Daten in numerische Werte, welche von den Statistik- Programmen zur Analyse benötigt werden. Siehe auch: vom Fragebogen zum Codeplan[9].
Codieren
C. bezeichnet die Zuordnung von festgelegten Schlüsseln (Zahlen oder Buchstaben) zu Merkmalsausprägungen für die Datenerfassung (z.B. bei Noten ’Sehr gut’ als 1, ’Gut’ als 2 etc.; oder bei Altersgruppen 1 für Kleinkinder, 2 für Jugendliche, 3 für Erwachsene, 4 für PensionistInnen).
Verweise:
[1] http://de.wikipedia.org/wiki/Induktive_Statistik
[2] http://de.wikipedia.org/wiki/Bestimmtheitsma%C3%9F
[3] Siehe Kapitel 3.5.1
[4] http://de.wikipedia.org/wiki/Clusteranalyse
[5] Siehe Kapitel 3.6.1.3
[6] Siehe Kapitel 3.4.5
[7] Siehe Kapitel 3.5.2.1.1
[8] http://de.wikipedia.org/wiki/Chi-Quadrat-Test
[9] Siehe Kapitel 2.2.3
5.2 D-F
Datenmatrix
Eine D. ist eine Anordnung der Daten, bei der die Untersuchungseinheiten in den Zeilen und die zu ihnen untersuchten Variablen in den Spalten eingetragen werden. Von oben nach unten könnten also z.B. die Versuchspersonen eingetragen werden, von links nach rechts ihre Körpergröße, ihre Leistungen, ihre Matrikelnummer etc. Eine Datenmatrix wird von jedem für statistische Zwecke verwendeten Programm zur Verwaltung der Daten verwendet.
Deskriptive Statistik
In der deskriptiven Statistik erstellt man Maßzahlen zur Charakterisierung von Daten, wie Lagemaße (z.B. Durchschnitt), Streuungsmaße (z.B. Quartile) oder Maße für den Zusammenhang von Variablen (z.B. Korrelation). Dazu gehört auch die grafische Aufbereitung der Daten und Ergebnisse in Form von Diagrammen. Im Gegensatz zur Analytischen Statistik beschäftigt sie sich nicht damit, von der Stichprobe unter Berücksichtigung verschiedener Wahrscheinlichkeiten auf die Grundgesamtheit zu schließen.
Dichotome Variable
Eine d.V. ist eine Variable, bei welcher nur zwei Ausprägungen möglich sind, wie z.B. lebendig/nicht lebendig; männlich/weiblich; bestanden/nicht bestanden. Jede stetige Variable kann zu dichotomen umgewandelt werden, wie z.B. differenziertes Einkommen zu ’unter 1000 €’ und ’über 1000 €).
Diskrete Variable
Eine d.V. ist eine Variable, bei welcher nur abzählbar viele Ausprägungen möglich sind, also eine unendliche feine Differenzierung nicht möglich ist (das wäre eine stetige Variable). Beispiele für eine d.V. sind die Punktzahlen eines Würfels, die Kinderzahlen von Familien, die Noten bei Prüfungen etc.
Dispersionsmaße
Siehe Streuungsmaße
Einseitige Hypothese (auch gerichtete Hypothese)
E. H. sind Hypothesen, welche eine bestimmte Richtung eines Zusammenhangs annehmen. Man nimmt also nicht nur an, dass z.B. die Körpergröße mit der Schuhgröße korreliert, sondern genauer, dass mit steigender Körpergröße eine größere Schuhgröße einhergeht. (siehe auch zweiseitige Hypothese).
Fehler 1. und 2. Art (auch Alpha- und Beta-Fehler)
In der Statistik arbeitet man mit Wahrscheinlichkeiten. Wir drücken dabei z.B. aus, dass unsere Nullhypothese bei einem Signifikanzniveau von 0,01 richtig ist, anders formuliert, bei einer Irrtumswahrscheinlichkeit von 1 %. Das bedeutet, dass in 1 % aller Fälle die Nullhypothese falsch sein wird, obwohl unsere Daten auf das gemessene Phänomen hindeuten. Das bezeichnet man als den Fehler der 1. Art = Die Nullhypothese stimmt nicht, obwohl unsere Daten die Nullhypothese bestätigen.
Der Fehler der 2. Art ist das Gegenteil. Die Nullhypothese wird zu Unrecht verworfen, weil die Daten (z.B. durch schlechte Auswahl der Mitglieder der Stichprobe) dazu anleiten.
Flächendiagramm
Das F. ist eine Diagrammform, bei welchem die Fläche zwischen Kurve und X- Achse durch Schraffierung oder Muster markiert wird.
5.3 G-I
Gaußsche Glockenkurve (auch Gaußverteilung)
siehe Normalverteilung
Geometrisches Mittel
siehe Mittel
Geschlossene Frage
Eine g. Fr. ist eine Frage mit vorgegebenen Antwortkategorien, z.B. ’Verdienen Sie ... A. unter 1000 €, B. über 1000 €’.
Geschichtete Stichprobe
Bei einer g. St. wird die Grundgesamtheit in Gruppen oder Schichten eingeteilt (z.B. FleischesserInnen und VegetarierInnen oder Männer und Frauen; Kinder, Jugendliche, Erwachsene, ältere Menschen). Man wird in der Regel versuchen (s. Repräsentativität), das in der Grundpopulation vorhandene Verhältnis der Gruppen in der Stichprobe nachzubilden. Man spricht dann von einer proportionalen Schichtung.
Grundgesamtheit (auch Grundpopulation)
Unter G. versteht man die Gesamtheit der Elemente, für welche die Aussagen der Untersuchung gelten sollen. Sie muss genau festgelegt werden. Erhebt man die Einstellungen von WienerInnen gegenüber ZuwandererInnen, so muss festgelegt werden, wer mit WienerInnen gemeint ist (ab welchem Alter; bei welchem rechtlichen Status, bei welcher Aufenthaltsdauer in der Stadt etc.). Da eine Vollerhebung nur selten möglich ist, wählt man in der Regel eine Stichprobe aus.
Gütekriterium
Unter G. versteht man Kriterien zur Abschätzung der Qualität und Seriösität wissenschaftlicher Forschung (Datenerhebung, Analyse etc.). Die wesentlichen G. sind Validität, Reliabilität und Objektivität.
Harmonisches Mittel
siehe Mittel.
Häufigkeit
Die Häufigkeit informiert, wie oft ein bestimmter Messwert auftritt. Man unterscheidet zwischen absoluter Häufigkeit (die gezählte Häufigkeit eines Messwerts, z.B. 18 Männer), die kumulierte Häufigkeit (die aufsummierte Häufigkeit bis zu einem bestimmten Niveau, z.B. 23 SchülerInnen hatten ein Gut oder Sehr Gut auf die Schularbeit), die prozentuelle Häufigkeit (in Prozent gemessen) bzw. die relative Häufigkeit (in Teilen von 1 gemessen).
Häufigkeitsverteilung
Unter einer H. versteht man eine tabellarische oder grafische Anordnung von Werten, bei der die jeweiligen Ausprägungen mit der dazugehörigen Häufigkeit vermerkt werden.
Histogramm
Ein H. ermöglicht die graphische Darstellung der Häufigkeitsverteilung quantitativer Merkmale. Die Daten werden in Klassen eingeteilt und auf einer Grundlinie aufgetragen. Über jeder Klasse wird ein Rechteck gezeichnet. Die Höhe des Rechtecks wird durch seine Häufigkeit bestimmt. Siehe auch: Histogramme[1].
Hypothese
Eine H. ist eine Annahme über die Beziehung zwischen zwei oder mehr Variablen, die mithilfe eines Untersuchungsverfahrens verifiziert oder falsifiziert werden kann. Siehe auch Nullhypothese.
Inferenzstatistik
Siehe Analytische Statistik
Interquartilsabstand
Als I. bezeichnet man die Differenz zwischen dem ersten und dem dritten Quartil. Grafisch wird er z.B. mit dem Boxplot dargestellt.
Intervallskalierung
Bei der I. können die Abstände zwischen den Ausprägungen metrischer Werte richtig interpretiert werden, jedoch gibt es keinen natürlichen Nullpunkt, sodass das Verhältnis der Werte nicht interpretiert werden kann. Der Abstand zwischen 12 und 13 Grad ist genauso groß wie der zwischen 34 und 35 Grad. Man kann jedoch nicht sagen, dass 10 Grad doppelt so heiß wie 5 Grad ist (es gibt einen absoluten Nullpunkt bei - 273 Grad, unsere gewohnte Null-Gradgrenze ist willkürlich und lässt sich nach unten unterschreiten).
Irrtumswahrscheinlichkeit
Unter I. versteht man die Wahrscheinlichkeit für das Auftreten des Fehlers 1. Art. Die I. ist somit die präzisierte Wahrscheinlichkeit, dass - obwohl die Daten einen bestimmten Schluss zulassen - dieser Schluss falsch ist. Als gängige Niveaus der Irrtumswahrscheinlichkeit nimmt man 5 %, 1 % und 1 ‰.
Verweise:
[1] Siehe Kapitel 3.6.1.5
5.4 J-M
Klasse
Unter einer K. versteht man eine Gruppe von Ausprägungen stetiger und diskreter Variablen, welche durch die Zusammenfassung benachbarter Werte entstehen. Eine Klasse wird von festgelegten Klassengrenzen begrenzt. Den Vorgang der Klassenbildung nennt man Klassierung oder Klassifikation. Eine Klassierung wird in der Regel verwendet, um die Darstellung enorm differenzierter Ausprägungen übersichtlicher zu gestalten (z.B. Zusammenfassung aller Einkommen in 0-500 €; eine zweite Klasse Einkommen bis 1000 €; eine dritte Klasse zwischen 1001-1500 € usw.). Siehe auch: Klassenbildung von Daten[1].
Klassifizerung (auch Klassierung).
Siehe Klasse.
Konfidenzinterall (auch Vertrauensintervall)
Aus Stichproben erhaltene Maßzahlen sind immer nur Annäherungen an die zugrundeliegenden, aber meist unbekannten Werte in der Grundpopulation. Man ermittelt daher Konfidenzintervalle, innerhalb welchen Bereichs sich der ’richtige’ Wert befindet. Diese Konfidenzintervalle hängen vom gewählten Signifikanzniveau ab. Wir erleben die Angabe derartiger Konfidenzintervalle an jedem Wahlsonntag, wenn bei den ersten Analysen des wahrscheinlichen Wahlergebnisses der/die Statistikexperte/in sagt, dass die Partei A mit zwischen 34,8 und 36,2 % der Stimmen rechnen kann. Mit wachsender Stichprobengröße (Auszählungsgrad) wird das Konfidenzintervall kleiner, weil immer mehr mit der Grundpopulation übereinstimmend, bis es bei Vollauszählung verschwindet. Siehe auch: Konfidenzintervall (Wikipedia)[2].
Kontingenztafel
Eine K. ist die tabellarische Darstellung der Häufigkeitsverteilung von zumindest zwei Merkmalen. Siehe Kreuztabelle.
Kontingenzkoeffizient
Ein K. ist eine Kennzahl für die Stärke des Zusammenhangs zwischen nominalskalierten Daten. Siehe auch: Kontingenzkoeffizient (Wikipedia)[3].
Korrelation
Unter K. versteht man den Zusammenhang zwischen zwei quantitativen Merkmalen. Die Stärke des Zusammenhangs wird durch den Korrelationskoeffizient ausgedrückt. Siehe auch: die Korrelation[4].
Korrelationskoeffizient
Der K. ist eine Kennzahl für den linearen Zusammenhang zwischen zwei quantitativen Merkmalen. Er liegt zwischen den Extremen -1 und +1. Wenn er positiv ist, bedeutet dies, dass ein hoher Wert der Variablen A mit einem hohen Wert der Variablen B einhergeht, genauso verhält es sich mit den niedrigen Werten. Ist der K. negativ, bedeutet dies, dass hohe Werte von Variable A mit niedrigen der Variable B einhergehen und umgekehrt.
Kovarianz
Die Kovarianz beschreibt den Zusammenhang zwischen zwei metrischen Merkmalen. Da sie nicht standardisiert ist, wird in der Regel statt ihr auf die von ihr abgeleitete Korrelation zurückgegriffen. Siehe auch: Kovarianz (Wikipedia)[5].
Kreisdiagramm (oder Tortendiagramm)
Das K. ist eine Diagrammform, welche sich besonders gut zur Darstellung von Anteilen vom Ganzen eignet. Häufigkeiten werden durch Kreissektoren wiedergegeben. Die Größe eines Tortenstücks entspricht dem relativen Anteil am Ganzen oder an 100 %.
Kreuztabelle (auch Kontingenztabelle, -tafel)
In einer K. stellt man die gemeinsame Häufigkeitsverteilung von zumindest zwei Variablen (nominal- oder ordinalskaliert) dar. Man versucht dabei, auffällige Unterschiede zwischen beobachteter Häufigkeit und der zu erwarteder Häufigkeit festzustellen und mittels des Chi-Quadrat-Tests wahrscheinliche Zusammenhänge zu überprüfen. Siehe auch: Kreuztabellen-Analyse[6].
Kumulative Häufigkeit (auch kumulierte H.)
siehe Häufigkeit
Lagemaße (auch Zentralwerte oder Maße der zentralen Tendenz)
Mit L. kann man den Schwerpunkt der Ausprägungen quantitativer Variabler zeigen.Die gebräuchlichsten Lagemaße sind das arithmetische Mittelt, der Median und der Modalwert. Siehe auch: Mittelwerte[7].
Liniendiagramm (auch Kurvendiagramm)
Man verwendet L., um den zeitlichen Verlauf von Entwicklungen zu zeigen. Siehe auch: Liniendiagramme[8].
Maßzahlen
M. zeigen charakteristische Eigenheiten quantitativer Variabler. Man unterscheidet Lagemaße und Streuungsmaße.
Median (auch Zentralwert)
Der Median kann bei mindestens ordinalskalierten Daten eingesetzt werden und bezeichnet jenes Element, welches in einer geordneten Reihe genau in der Mitte liegt. D.h. dass es oberhalb von ihm genauso viele (größere) Einträge wie unterhalb von ihm gibt.
Der Median eignet sich besonders gut, wenn Ausreißer das arithmetische Mittel verzerren.
Merkmal (auch Variable)
Unter einem M. versteht man Eigenheiten des Untersuchungsobjekts, deren Ausprägungen variieren können (im Gegensatz zu Konstanten).
Messniveau (auch Skalenniveau)
Unter Messen versteht man im weitesten Sinne die Zuordnung von Zahlen zu Beobachtung. Anhand des Messniveaus legt man fest, welche Interpretationen unterschiedlicher Ausprägungen sinnvoll sind, welche Verfahren angewendet werden dürfen. Es gibt vier Messniveaus: Nominal-, Ordinal-, Intervall- und Ratioskala. Die beiden ersten beziehen sich auf nicht metrische Variablen, die beiden letzten auf metrische Variablen.
Metrik
Unter M. versteht man ein definiertes System von Kennzahlen/Maßeinheiten (z.B. Liter, Kilometer, Minuten).
metrisch
Als metrisch werden Variable bezeichnet, wenn der Abstand zwischen zwei Ausprägungen der Variablen interpretiert werden kann, wenn also der Abstand zwischen 12 und 15 genauso großist wie der Abstand zwischen 23 und 26. Metrische Variable sind daher entweder intervall- oder proportionalskaliert. Nichtmetrische Variablen sind nominal- oder ordinalskaliert.
Mittel
Sammelbegriff für verschiedene Lagemaße, wie z.B. das arithmetische Mittel, das harmonische Mittel[9], das geometrische Mittel[10].
Mittelwert (auch Arithmetisches Mittel)
Der M. eines metrischen Merkmals ist ein Lagemaß und entspricht der Summe aller Werte geteilt durch deren Anzahl.
Modalwert (auch Modus)
Der M. ist ein Lagemaß. Er bezeichnet den am häufigsten vorkommenden Wert.
Modus (siehe Modalwert)
Multivariate Verfahren (oder m. Analyse)
Unter M. V. versteht man Verfahren, bei welchen mindestens drei Variablen und deren Wechselbeziehungen analysiert werden. Siehe auch: Multivariate Analyse (Wikipedia)[11].
Verweise:
[1] Siehe Kapitel 3.2.3
[2] http://de.wikipedia.org/wiki/Konfidenzintervall
[3] http://de.wikipedia.org/wiki/Kontingenzkoeffizient
[4] Siehe Kapitel 3.5.3
[5] http://de.wikipedia.org/wiki/Kovarianz_%28Stochastik%29
[6] Siehe Kapitel 3.5.2
[7] Siehe Kapitel 3.3
[8] Siehe Kapitel 3.6.1.2
[9] Siehe Kapitel 3.3.5
[10] Siehe Kapitel 3.3.4
[11] http://de.wikipedia.org/wiki/Multivariate_Analyse
5.5 N-P
Nichtparametrische Verfahren (auch parameterfreie Verfahren)
Als N.T. werden alle statistischen Verfahren bezeichnet, welche nicht an bestimmte Verteilungsformen (wie der Normalverteilung) gebunden sind. Solche Tests sind z.B. der Chi-Quadrat-Test, der Wilcoxon-Test (Wikipedia)[1] und der Mann-Whitney (Wikipedia)[2]-Test.
nominal
Merkmale werden als nominal bezeichnet, wenn ihre Ausprägungen nicht sinnvoll oder ’natürlich’ gereiht werden können (wie z.B. Farben, Hobbies, Namen). Sie sind nominalskaliert[3]. Siehe Messniveau.
Normalverteilung (auch Gaußverteilung)
Die N. in Form der Gaußschen Glockenkurve ist eine Verteilungsform mit folgenden Merkmalen: sie ist unimodal (hat nur einen Gipfel); der Gipfel befindet sich in der Mitte (d.h. die in der Mitte des Messspektrums auftretenden Ausprägungen kommen auch am häufigsten vor); sie sind symmetrisch (links wie rechts vom Mittelwert fallen die Häufigkeiten gleichmäßig ab); die Lagemaße wie Modalwert, Mittelwert und Median stimmen (fast) annähernd überein. Innerhalb des Bereichs Mittelwert ± der Standardabweichung s liegen ca. 68 % aller Messwerte. Siehe auch: Normalverteilung (Wikipedia)[4].
Nullhypothese
Unter einer N. versteht man die Annahme bei statistischen Tests, dass ein postulierter Zusammenhang oder Unterschied nicht besteht. Mit geeigneten Verfahren wird untersucht, ob die Unterschiede oder Zusammenhänge bei einem gewählten Signifikanzniveau noch als zufällig erklärt werden können. Wird das Signifikanzniveau erreicht, wird die Nullhypothese verworfen und die Alternativhypothese angenommen.
Offene Frage
Bei o. Fr. werden im Gegensatz zu geschlossenen Frage keine Antwortkategorien vorgegeben. Daher ist die Auswertung o. Fr. deutlich aufwendiger, weil sie erst interpretiert und eingeordnet werden müssen.
Objektivität
Unter O. versteht man eine Grundanforderung an Methoden der Datenerhebung. Die Untersuchenden müssen versuchen sicherzustellen, dass andere ForscherInnen bei gleichen Erhebungsmethoden zum gleichen Ergebnis kommen. Dadurch soll eine Unabhängigkeit der Ergebnisse von den Erhebenden angestrebt werden. Im weiteren Sinne bezieht sich O. auch auf die Auswertung der Daten und deren Interpretation. Siehe auch andere Gütekriterien von Datenerhebungen, wie die Variablität und Validität.
Operationalisierung
Unter O. versteht man eine möglichst exakte Festlegung der Vorgangsweise bei der Datenerhebung, wie z.B. Frageformulierungen, Anwortvorgaben, Anweisungen an InterviewerInnen usw. Die O. gibt genau an, wie ein bestimmtes Phänomen gemessen werden soll (wie z.B. die angenommene Ablehnung bestimmter Zuwanderergruppen). Die O. inkludiert alle Vorgänge von der Formulierung einer Hypothese, ihrer Umsetzung in konkrete Fragen und die Aufnahme der Daten.
ordinal
Eine Variable gilt als ordinal, wenn ihre Ausprägungen natürlich geordnet werden können, nicht aber die Unterschiede zwischen den Ausprägungen. So weiß man, dass eine Schulnote 1 besser als die Schulnote 2 ist, aber es ist nicht gesichert, dass der Schüler mit der Note 1 den Schüler mit der Note 2 im gleichen Maße übertrifft wie ein Schüler mit der Note 4 einen Schüler mit der Note 5.
Ordinalskalierung
Messniveau ordinaler Daten (siehe ordinal).
Population
Gesamtmenge aller Beobachtungseinheiten
p-Wert (auch Überschreitungswahrscheinlichkeit)
Der p. Wert (Kurzform von probability) gibt bei statistischen Tests die Wahrscheinlichkeit an, mit welcher eine gefundene Kennzahl rein zufällig auftreten könnte. Man legt vor der Durchführung eines Tests ein Signifikanzniveau fest, z.B. p= 0,05. Ergibt sich ein p-Wert von kleiner als 0,05, dann ist die Nullhypothese mit einer Irrtumswahrscheinlichkeit von kleiner als 5 % zu verwerfen.
Parameter
P. sind Kennzahlenn, welche eine Grundpopulation charakterisieren. Dazu zählen insbesonders die Lagemaße und die Streuungsmaße. Da sie in der Regel für die Grundpopulation nicht bekannt sind, müssen sie auf der Basis von Stichproben hochgerechnet werden.
Parametrische Verfahren
Unter p. V. versteht man statistische Tests, welche das Vorliegen einer bestimmten Verteilungsform mit den dafür typischen Parametern erfordern. Besonders häufig wird die Normalverteilung als Grundbedingung gesehen.
Partielle Korrelation (auch Partialkorrelation)
Eine P.K. ist das Ausmaß des Zusammenhangs (Korrelation) zwischen zwei Variablen, wobei gleichzeitig versucht wird, den Einfluss einer dritten Variablen auf diesen Zusammenhang herauszurechnen. Siehe auch: Scheinkorrelation und Störvariable[5].
Pearson’scher Korrelationskoeffizient
Siehe Produkt-Moment-Korrelation
Perzentil
Siehe Quantil
Proportionalskala (auch Verhältnisskala)
Eine P. gehört zu den vier wesentlichen Messniveaus (Messskalen) und liegt dann vor, wenn bei numerischen Daten ein absoluter Nullpunkt vorliegt. Bei einer P. können nicht nur die Abstände zwischen Ausprägungen interpretiert werden, sondern auch ihr Verhältnis. So ist z.B. ein Baum von 3 Metern Höhe doppelt so hoch wie ein Baum von 1,5 Meter Höhe.
Population
Siehe Grundpopulation
Pretest
Unter einem P. versteht man eine der Befragung der Stichprobe per Fragebogen vorausgehende Abtestung desselben durch Probeinterviews, um Schwächen im Vorfeld zu eliminieren. Man untersucht dabei z.B., ob die Fragen verständlich sind, wie sie interpretiert werden, ob alle Fragen zufriedenstellende Antworten bringen, ob die Befragten bereit sind, alle Fragen zu beantworten, ob die Befragten den Zeitaufwand für die Ausfüllung des Fragebogens akzeptieren etc.
Produkt-Moment-Korrelation (auch Pearson’scher Korrelationskoeffizient)
Die P.M.-Korrelation ist eine Form der Korrelation und zeigt den Zusammenhang zwischen zwei standardisierten Variablen, die beide metrisch und normalverteilt sein müssen. Siehe auch: Maßkorrelation[6].
Punktwolke
siehe Streudiagramm
Verweise:
[1] http://de.wikipedia.org/wiki/Wilcoxon-Rangsummentest
[2] http://de.wikipedia.org/wiki/Mann-Whitney-Test
[3] Siehe Kapitel 3.1.2.2
[4] http://de.wikipedia.org/wiki/Normalverteilung
[5] Siehe Kapitel 3.5.3.4.3
[6] Siehe Kapitel 3.5.3.1
5.6 Q-R
Quantitativ
Eigenschaft, dass die Ausprägung von Elementen in Zahlen wiedergegeben werden kann, wobei eine größere Zahl auch eine größere Ausprägung impliziert.
Quantil
Unter Q. versteht man Orientierungspunkte einer statistischen Verteilung; sie dienen als Streuungsmaße zur Beschreibung der Verteilung. Dabei wird die Verteilung stets in gleich große Teile aufgeteilt. Bei vier gleichen Teilen spricht man von Quartilen, bei fünf von Quintilen, bei zehn von Dezilen und bei 100 von Perzentilen. Besonders gerne verwendet werden die Quartile. Das erste Quartil gibt den Wert an, unterhalb desselben sich 25 % der Einträge befinden. Das zweite Quartil oder Median gibt den Wert an, unterhalb desselben sich 50 % der Einträge befinden usw.
Quantifizierung
Unter Qu. versteht man die numerische Beschreibung von Merkmalsausprägungen einer Variablen auf Basis von Messungen oder Zählungen.
quantitativ
Ein Merkmal wird quantitativ genannt, wenn es sich (z.B. durch Messen), zahlenmäßig erfassen lässt. Quantitative Merkmale werden in diskrete und stetige Merkmale unterteilt.
Quartil
Siehe Quantil
Quartilabstand
Siehe Interquartilabstand
Range (auch Variationsweite, Spannweite)
Unter R. versteht man den Abstand zwischen dem kleinsten und dem größten aufgetretenen Wert bei mindestens ordinalskalierten Daten. Die Range bei gemessenen Körpergrößen wäre demnach z.B. 2,18 m(größter Wert) - 1,54 m(kleinster Wert), also 64 cm.
Rangkorrelation
Form der Korrelation, bei welcher nicht die Merkmalsausprägungen, sondern deren Rangzahlen verwendet werden. Dabei werden im wesentlichen zwei Verfahren verwendet, Spearman´s Rho und Kendall’s Tau. Siehe auch: die Korrelation[1].
Rangzahlen
Man erhält sie, wenn quantitative Daten größenmäßig geordnet werden und die geordneten Werte, mit 1 beginnend, fortlaufend nummeriert. Im Falle gleicher Ursprungsgröße müssen die Rangplätze gemittelt werden. Ein Beispiel: Die Punktezahl 12 tritt sowohl auf den Rangplätzen 13 wie 14 auf. Beide Rangplätze erhalten daher die gemittelte Rangzahl 13,5 (beide Zahlen addiert und durch die Anzahl der Werte, also 2, dividiert).
Regression
Unter R. versteht man Verfahren, welche es erlauben, Werte einer anderen Variablen vorherzusagen, wenn der Wert einer bestimmten Variablen bekannt ist. Siehe auch: die Regression[2].
Relative Häufigkeit
Während die absolute Häufigkeit einer Ausprägung anzeigt, wie oft dieser Wert insgesamt im Datensatz erscheint, gibt die r. H. an, wie hoch sein Anteil verglichen mit der Gesamtzahl der gültigen Einträge ist. Siehe auch: Häufigkeitstabelle[3].
Reliabiltität (auch Zuverlässigkeit)
R. ist eines der drei Gütekriterien bei Messungen. Dieses fordert, dass die Messinstrumente bei einer Wiederholung der Messung bei gleichbleibenden Bedingungen das gleiche Ergebnis erbringen sollten.
Neben der Validität (Gültigkeit) das zweite zentrale Qualitätskriterium bei Messungen. Meint, dass Messinstrumente bei wiederholter Messung unter gleichen Bedingungen auch das gleiche Ergebnis produzieren müssen. Siehe auch: Reliabilität (Wikipedia)[4].
Repräsentativität
Unter R. versteht man, dass bei der Auswahl der Elemente der Stichprobe die Zusammensetzung der Grundpopulation nachgebildet wird. Wenn z.B. 2/3 der Zuwanderer aus Afrika in Österreich männlich sind, sollten dementsprechend auch 2/3 der Befragten in der Stichprobe männlich sein, will man den Bedingungen der Repräsentativität genügen.
Robust
Bezeichnung für Verfahren, welche bezüglich vorhandener Ausreißer kaum empfindlich sind, wie z.B. der Median.
Rohdaten
statistisch nicht veränderte Untersuchungsergebnisse, welche die ursprüngliche Merkmalsausprägung anzeigen (z.B. die Zahl der Punkte bei einem Eignungstest statt deren Umsetzung in Noten).
Verweise:
[1] Siehe Kapitel 3.5.3
[2] Siehe Kapitel 3.5.4
[3] Siehe Kapitel 3.2.2
[4] http://de.wikipedia.org/wiki/Reliabilit%C3%A4t
5.7 S-T
Säulendiagramm
Siehe Balkendiagramm.
Schichtung
Unter Sch. versteht man eine Methode bei der Auswahl der Stichprobe. Die Grundpopulation wird in Schichten (Wikipedia)[1] zerlegt (in dieser gibt es z.B. 40 % Männer und 60 % Frauen; in dieser gibt es 26 % unter 25, 38 % zwischen 26- 50 und 36 % darüber). In der Stichprobe versucht man das Verhältnis dieser Schichten der Grundpopulation nachzubilden.
Schließende Statistik
s. Analytische Statistik
Selektion
Bei der Selektion schränkt man die Grundgesamtheit, für die eine bestimmte Hypothese geprüft werden soll, auf eine Teilgesamtheit von Beobachtungseinheiten ein.
Signifikanz
Unter S. versteht man ein statistisch überprüftes Urteil über die Haltbarkeit einer Hypothese. Da man nur selten eine Vollerhebung machen kann, ist ein Ergebnis einer Stichprobe stets vom Risiko begleitet, dass es vom Ergebnis der Grundpopulation abweichen könnte. Man überprüft daher die Wahrscheinlichkeit, dass ein gefundenes Ergebnis rein zufällig entstanden sein könnte. Als Maßstäbe nimmt man sogenannte Signifikanzniveaus, meist von 5 % oder p=0,05 oder 1 % oder p=0,01. Unterschreitet die erhaltene Wahrscheinlichkeit den letzten Wert, so könnte eine statische Aussage lauten: "Der Zusammenhang zwischen den Variablen A und B ist statistisch signifkant auf dem 1%-Niveau." Ein wichtiger Test zur Abschätzung der Signifikanz der Zusammenhänge in Kreuztabellen ist z.B. der Chi- Quadrat- Test. Siehe auch: Statistische Signifikanz (Wikipedia)[2].
Signifianzniveau
Das Signifikanzniveau ist synonym für die obere Grenze der Irrtumswahrscheinlichkeit eines statistischen Tests.
Siehe auch Signifikanz
Skala
S. (ital. Treppe) bezeichnet eine Folge von Positionen, die unterschiedliche Ausprägungsgrade eines Merkmals anzeigen (z.B. die Temperatur eines Körpers in Celsius, Lieblingszeitschriften durch die Angabe des jeweiligen Titels etc.). Siehe Messniveau.
Skalenniveau
siehe Messniveau
Spannweite
Siehe Range.
Spearman’s Rho (oder Spearmans Korrelationskoeffizient)
Falls zwei Merkmale ordinal verteilt sind, kann man den Rangkorrelationskoeffizienten R (oder Spearmans Rho) mithilfe einer Produkt- Moment-Korrelation der Rangplätze berechnen. Siehe auch: Rangkorrelation[3] .
Stabdiagramm
Siehe Balkendiagramm.
Standardabweichung
Die St. s ist ein Kennwert, um die Variabilität (Streuung) eines Merkmals zu kennzeichnen. Sie wird als Wurzel aus der Varianz erreichnet. In einer Normalverteilung liegen im Bereich des Arithmetischen Mittels ± s ungefähr 68 % aller Ergebnisse. Siehe auch: Standardabweichung (Wikipedia)[4].
Standardisiertes Interview
Das st. I. ist eine Interviewform, bei welcher alle Details der Befragung (was soll man wie fragen, wie soll man reagieren, welche Zusatzinformationen darf man liefern etc.) genau festgelegt wurden, um den Einfluss der InterviewerInnen möglichst gering zu halten.
stetig
Ein quantitatives Merkmal wird st. genannt, wenn es alle Werte innerhalb eines Intervalls annehmen kann. So kann z.B. eine Körpergröße beliebig fein gemessen werden, in cm, in mm und bei Kleinstlebewesen sogar noch deutlich darunter. Diskrete Variable hingegen können nur bestimmte und abzählbare Werte einnehmen (Beispiel Würfel).
Stichprobe
Unter einer St. versteht man die Auswahl an Beobachtungseinheiten aus einer definierten (Grund)Population. Eine Stichprobe sollte diese Grundpopulation unverzerrt wiederspiegeln, z.B. durch das Modell der Repräsentativität.
Störvariable (oder Störgrößen)
Unter Störvariablen versteht man Variable, welche zusätzlich zu einer unabhängigen Variablen einen nicht einkalkulierten Einfluss auf eine abhängige Variable ausüben. Untersucht man z.B. den Zusammenhang zwischen Glatzenbildung und Einkommen, so wird man häufig auf eine höhere Korrelation kommen. Diese hängt mit einer nicht untersuchten Störvariable zusammen, nämlich dem Alter, mit dem sowohl Glatzenbildung wie auch Einkommen normalerweise hoch korrelieren.
Die Existenz von Störvariablen ist besonders bei der Untersuchung von Korrelationen kritisch zu untersuchen.
Streudiagramm (auch Scatterplot)
Ein St. zeigt graphisch den Zusammenhang zwischen zwei stetigen Merkmalen, wobei eine Punktwolke aus den Schnittpunkten der jeweiligen Ausprägungen der Variablen X und Y gebildet wird. Streudiagramme bieten eine gute Abschätzmöglichkeit für mögliche Korrelationen.
Streuungsmaße (auch Dispersionsmaße)
Streuungsmaße geben an, in welchen Bereichen die Daten liegen bzw. um die Lagemaße streuen. Sie sind Kennwerte zur Charakterisierung einer Verteilung. Sie sind Indikatioren für die Variabilität von Merkmalen, wie z.B. von deren Abstand zum Arithmetischen Mittel. Wichtige Streuungsmaße sind die Standardabweichung, die Varianz oder der Quartilabstand.
Tau (auch Kendall’s Tau)
Form der Korrelation. Maß für den Zusammenhang zwischen ordinalskalierten Daten, besonders bei kleinen Zahlen. Siehe auch: Rangkorrelation Tau[5].
Tortendiagramm
Siehe Kreisdiagramm
Verweise:
[1] http://de.wikipedia.org/wiki/Soziale_Schichtung
[2] http://de.wikipedia.org/wiki/Statistische_Signifikanz
[3] Siehe Kapitel 3.5.3.2
[4] http://de.wikipedia.org/wiki/Standardabweichung
[5] Siehe Kapitel 3.5.3.3
5.8 U-Z
unabhängig
Eine Variable ist unabhängig, wenn sie in einer Untersuchung variiert werden kann, um ihre Auswirkungen auf eine abhängige Variable zu erfassen (z.B. Menge von Düngemitteln: unabhängige Variable, Ernte-Ergebnis: abhängige Variable).
univariat
Als u. werden Methoden und Kennzahlen bezeichnet, die sich auf eine einzige Variable beziehen.
Urliste
Die U. ist die ungeordnete Zusammenstellung des Datenmaterials. Siehe auch: Listen und Tafeln[1].
Validität (auch Gültigkeit)
Die V. gehört zu den sogenannten Gütekriterien für die Qualität einer Datenerhebung. Sie bezeichnet die Eigenschaft, wirklich das zu messen, was bei der Untersuchung gemessen werden soll. Wenn z.B. die Fragen eines Fragebogens nur ungenügend geeignet sind, die Hypothesen zu überprüfen, dann ist die Validität in Frage gestellt. Siehe auch: Validität (Wikipedia)[2].
Variable
Eine Variable ist ein in verschiedenen Ausprägungen vorhandenes Merkmal eines Untersuchungsgegenstandes: z.B. Geschlecht: männlich/weiblich; Größe gemessen in cm.
Variationsweite (siehe Range).
Varianz
Die V. ist ein Maß für die Variabilität bzw. die Streuung der Ausprägungen von Variablen und Ausgangswert für die Standardabweichung. Siehe auch: Varianz (Wikipedia)[3].
Verhältnisskala
Siehe Proportionalskala
Verteilung
Siehe Häufigkeitsverteilung
Vertrauensintervall (auch Konfidenzintervall)
Siehe Konfidenzintervall
Vierfeldertafel (Form der Kreuztabelle)
Eine V. ist die Anordnung zweier dichotomer Variablen in einer Tabelle mit zwei Spalten und zwei Zeilen, sodass jede Ausprägung jeder Variablen mit jeder Ausprägung der anderen gekreuzt wird.
Vollerhebung
Eine V. liegt vor, wenn alle Elemente einer Grundpopulation befragt werden und nicht nur eine Auswahl (eine Stichprobe) derselben. Eine V. ist dementsprechend nur bei einer kleineren Grundpopulation möglich.
Wahrscheinlichkeit
Unter W. versteht man die Einstufung von Phänomenen nach dem Grade ihrer Gewissheit. Die W. p wird mit Werten zwischen 0 (Unmöglichkeit) und 1 (Sicherheit des Auftretens) wiedergegeben. Siehe auch: Wahrscheinlichkeit (Wikipedia)[4].
Zentralwert
Siehe Median
Zusammenhang
Mit einem Z. bezeichnet man, dass zwischen den Ausprägungen zweier Variablen eine systematische Entsprechung besteht. Siehe Korrelation.
Zweiseitige Hypothese
Bei einer z. H. nimmt man an, dass zwischen zwei Variablen oder zwischen zwei Teilgruppen ein Zusammenhang besteht. Man nimmt jedoch nicht von vornherein an, dass dieser Zusammenhang nur in einer bestimmten Richtung besteht. Beispiel: Die Annahme ist, dass sich das Wetter auf die Arbeitslust auswirkt, wobei man nicht von vornherein einschränkt, ob ein schöneres Wetter zu einer größeren Arbeitslust oder zu einer geringeren führen wird. Bei der einseitigen H. würde nur eine Richtung untersucht werden: Sorgt schöneres Wetter für eine größere Arbeitslust?
Verweise:
[1] Siehe Kapitel 3.2.1
[2] http://de.wikipedia.org/wiki/Validit%C3%A4t
[3] http://de.wikipedia.org/wiki/Varianz
[4] http://de.wikipedia.org/wiki/Wahrscheinlichkeit
6. Literatur, Ressourcen und Links
In diesem Bereich finden Sie Hinweise auf hochwertige Nachschlagswerke zu den angeschnittenen Bereichen sowie eine Selektion von Weblinks.
6.1 Quantitative Forschungsmethoden
Atteslander P. 2000. Methoden der empirischen Sozialforschung, 9. edn. deGruyter.
Diekmann A. 2001. Empirische Sozialforschung. Grundlagen, Methoden, Anwendungen, 7 edn. Rowohlt, Reinbeck bei Hamburg.
Fahrmeir, Ludwig & Künstler, Rita & Pigeo, Iris & Tutz, Gerhard. 2004. Statistik. Springer, Berlin - Heidelberg.
Friedrichs J. 1990. Methoden empirischer Sozialforschung, 14. edn. Westdeutscher Verlag, Opladen.
Götz R. & Pötter U. 2001. Grundzüge der sozialwissenschaftlichen Statistik. Juventa, Weinheim und München.
Krämer, Walter. 2000. So lügt man mit Statistik. Piper- Verlag.
Kromrey, H. 2000. Empirische Sozialforschung. Modelle und Methoden der standardisierten Datenerhebung und Datenauswertung. Leske und Budrich, Opladen.
Müller-Bendedict V. 2001. Grundkurs Statistik in den Sozialwissenschaften. Westdeutscher Verlag, Opladen.
Schnell, Rainer & Hill, Paul B. & Esser, Elke. 1999. Methoden der empirischen Sozialforschung. Oldenbourg, München, Wien.
Zöfel, Peter. 2003. Statistik für Wirtschaftswissenschaftler. Pearson Studium, München.
Weblinks:
Basis-Statistik (FAES)[1], 05.02.2007.
HyperStat Online[2], 05.02.2007.
Help with Statistics (University of Leicester)[3], 21.11.2019.
Kromrey, Helmut. 1994. Empirische Sozialforschung[4], 21.11.2019.
Lohninger, H. Grundlagen der Statistik[5], 05.02.2007.
Neuwirth, Erich. 1997. Statistik für StatistikerInnen,[6] 05.02.2007.
Rost, Jürgen. 2003. Zeitgeist und Moden empirischer Sozialforschung[7]. In Forum Qualitative Sozialforschung 4/2, 05.02.2007.
Wahrscheinlichkeitstheorie und Statistik (Uni Osnabrück)[8], 21.11.2019.
TU-Graz Statistik-Grundkurs[9], 05.02.2007.
Verweise:
[1] http://www.faes.de/Basis/Basis-Statistik/basis-statistik.html
[2] http://davidmlane.com/hyperstat/
[3] https://www2.le.ac.uk/offices/ld/help-with/stats
[4] https://obv-at-ubw.userservices.exlibrisgroup.com/view/action/uresolver.do?operation=resolveService&package_service_id=16033772210003332&institutionId=3332&customerId=3330
[5] http://www.statistics4u.info/fundstat_germ/index_a.html
[6] http://tud.at/uni/stat1.htm
[7] http://www.qualitative-research.net/index.php/fqs/article/view/723
[8] https://www.mathematik.uni-osnabrueck.de/fileadmin/mathematik/downloads/2009_wust_meyer.pdf
[9] http://hfi.uni-graz.at/hfi/lehre/archiv/gruku_2001_2002/ab09/frame09.htm
6.2 Fragebogen-Abfrage
Bücher:
Allerbeck, K. & W. Hoag. 1985. Zur Methodik der Umfragen. Frankfurt am Main, Johann Wolfgang von Goethe- Universität.
Converse, J.M. & S. Presser. 1986. Survey Questions. Handcrafting the Standardized Questionnaire. Beverly Hills, Sage.
Porst, Rolf. 1998. Im Vorfeld der Befragung: Planung, Fragebogenentwicklung, Pretesting. ZUMA- Arbeitsbericht 98/02, Mannheim.
Sudman, S. & N.M. Bradburn 1983. Asking Questions. San Francisco, Jossey-Bass.
Weblinks:
Michael Vonrüden. 2002. Internetbasierte Umfragen[1]. (PDF-Dokument), 05.02.2007.
Verweise:
[1] http://www.michael-vonrueden.de/res/Internet-basierte-Umfrageformen.pdf
6.3 Methoden
Korrelation und Regression
Die Korrelation[1] von Merkmalen. (PDF-Dokument), 05.02.2007.
Jörg Kovarianz und Korrelation[2]. In Psychologie-Seiten.de, 21.11.2019
Verschiedene Methoden
Berger, Klaus. Materialen für Mathe-Online[3], 05.02.2007.
Verweise:
[1] http://www.mathe-online.at/materialien/klaus.berger/files/regression/korrelation.pdf
[2] https://www.psychologie-seiten.de/psychologische-methodenlehre/48-kovarianz-und-korrelation.html
[3] http://www.mathe-online.at/materialien/klaus.berger/
6.4 Repräsentativität
Höpflinger, François. 2011. Standardisierte Erhebungen - methodische Hinweise zu Umfragen[1], 21.11.2019.
Verweise:
[1]http://www.hoepflinger.com/fhtop/Umfragemethodik.pdf
6.5 Statistik-Software
Bücher:
Bühl, Achim. 2006. SPSS 14. Einführung in die moderne Datenanalyse. Pearson Studium, München.
Wittenberg R. & Cramer Hans. 2003. Datenanalyse mit SPSS für Windows. UTB, Stuttgart.
Links:
Ludwig-Mayerhofer, Wolfgang. Internet Guide to SPSS for Windows[1], 21.11.2019
Verweise:
[1] http://wlm.userweb.mwn.de/SPSS/
6.6 Terminologie
Links zur Terminologie quantitativer Forschungsmethoden
FAES.DE. Basislexikon[1], 05.02.2007.
Lernstats. Glossar[2], 05.02.2007.
Ludwig-Mayerhofer, Wolfgang. Internet Lexikon der Empirischen Sozialforschung[3], 21.11.2019
Verweise:
[1] http://www.faes.de/Basis/Basis-Lexikon/basis-lexikon.html
[2] http://www.lernstats.de/php/glossar.php?lang=de&
[3] http://wlm.userweb.mwn.de/Ilmes/
6.7 Statistik-Quellen
Hier finden Sie die Webseiten verschiedener Institutionen, die laufend Statistiken erstellen:
Statistik-Austria[1], 05.02.2007.
Eurostat - Statistikamt der Europäischen Union[2], 16.11.2009.
Statistiken der Stadt Wien[3], 05.02.2007.
United Nations Statistics Division[4], 05.02.2007.
World Bank Data[5], 05.02.2007.
FAO Statistics[6], 19.01.2010.
UNDP - Human Development Report[7], 16.11.2009.
Verweise:
[1] http://www.statistik.at/
[2] https://ec.europa.eu/eurostat
[3] http://www.wien.gv.at/statistik/
[4] https://unstats.un.org/home/
[5] https://data.worldbank.org/
[6] www.fao.org/faostat/en/#home
[7] http://hdr.undp.org/en/data